Лабораторная работа по дискретной математике. ЛР1 дискрет мой. Лабораторная работа 1 по дисциплине Дискретная математика Вариант 7 Направление 27. 03. 04
 Скачать 264.71 Kb. Скачать 264.71 Kb.
|
|
Томский межвузовский центр дистанционного образования Томский государственный университет систем управления и радиоэлектроники (ТУСУР) Кафедра компьютерных систем в управлении и проектировании (КСУП) Лабораторная работа № 1 по дисциплине «Дискретная математика» Вариант 7 Направление 27.03.04 . Задание 1. По матрицам (рис. 2; 3) построить диаграммы графов, определив предварительно вид данных матриц. Задание 2. Методами поиска «в глубину» и «в ширину» выделить в графе (рис. 1) между его вершинами наибольший минимальный маршрут. Задание 3. Для каждой пары вершин графа (рис. 1) аналитическим способом вычислить количество маршрутов длины, равной 4, и выделить те пары вершин, для которых их количество ≥ 3, но не более 10. Выписать эти маршруты для какой-либо из выделенных пар. В описании маршрутов указывать вершины и рёбра, входящие в него. Задание 4. Построить матрицу метрики графа (рис. 1). Задание 5. С помощью алгоритма Магу—Вейсмана выполнить правильную раскраску вершин графа с минимальным количеством цветов. Задание 6. Определить число вершинного покрытия графа (рис. 1). Задание 7. Определить содержит ли граф (рис. 1) эйлерову цепь или эйлеров цикл? Ответ обосновать. 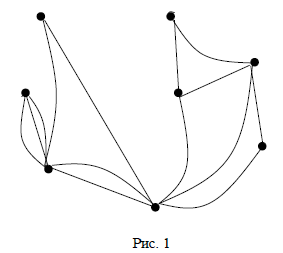 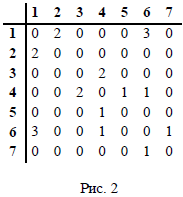 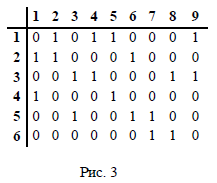 Задание 8. Аналитическим способом определить число компонент связности графа  Задание 1 По матрицам (рис. 2; 3) построить диаграммы графов, определив предварительно вид данных матриц. Решение На рисунке 2 задана матрица смежности. Граф содержит 7 вершин, является неориентированным и содержит кратные ребра.  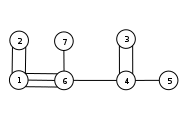 На рисунке 3 изображена матрица инцидентности. Граф содержит 6 вершин и 9 ребер,является неориентированным.  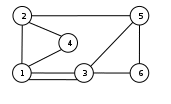 Задание 2. Методами поиска «в глубину» и «в ширину» выделить в графе между его вершинами наибольший минимальный маршрут. 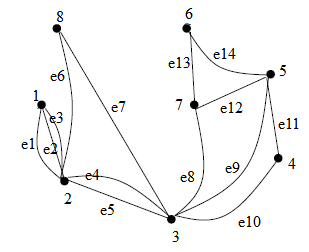 Решение Поиск в глубину: Начинаем с вершины 1. Из вершины 1 можем перейти в вершину 2 по ребру e1 Из вершины 2 можем перейти в вершину 3 по ребру e4 Из вершины 3 можем перейти в вершину 4 по ребру e10 Из вершины 4 можем перейти в вершину 5 по ребру e11 Из вершины 5 можем перейти в вершину 6 по ребру e14 Из вершины 6 можем перейти в вершину 7 по ребру e13 У вершины 7 нет смежных непосещенных вершин, вернемся к вершине 6. У вершины 6 нет смежных непосещенных вершин, вернемся к вершине 5. У вершины 5 нет смежных непосещенных вершин, вернемся к вершине 4. У вершины 4 нет смежных непосещенных вершин, вернемся к вершине 3. Из вершины 3 можем перейти в вершину 8 по ребру e7 У вершины 8 нет смежных непосещенных вершин, вернемся к вершине 3. У вершины 3 нет смежных непосещенных вершин, вернемся к вершине 2. У вершины 2 нет смежных непосещенных вершин, вернемся к вершине 1. У вершины 1 нет смежных непосещенных вершин. Алгоритм закончен. Получили дерево путей 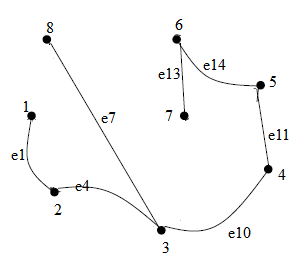 Максимальный путь: 1→2→3→4→5→6→7 Поиск в ширину:  Начинаем с вершины 1. Из вершины 1 можем попасть в вершину 2, добавим ее в очередь: (2). Из вершины 2 можем попасть в вершины 3 и 8, добавим их в очередь и удалим 2: (3 8) Из вершины 3 можем попасть в вершины 4, 5 и 7, добавим их в очередь и удалим 3: (8 4 5 7) У вершины 8 нет непосещенных смежных вершин, удаляем ее из очереди: (4 5 7) У вершины 4 нет непосещенных смежных вершин, удаляем ее из очереди: (5 7) Из вершины 5 можем попасть в вершину 6, добавим ее в очередь и удалим 5: (7 6) У вершины 7 нет непосещенных смежных вершин, удаляем ее из очереди: (6) У вершины 6 нет непосещенных смежных вершин, удаляем ее из очереди: ( ). Очередь пуста. Алгоритм закончен. Дерево путей 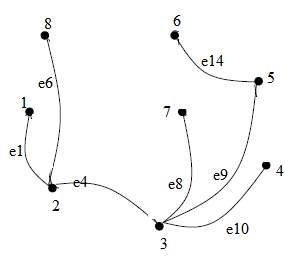 Максимальные пути: 8→2→3→5→6 и 8→2→3→5→6 Задание 3. Для каждой пары вершин графа (рис. 1) аналитическим способом вычислить количество маршрутов длины, равной 4, и выделить те пары вершин, для которых их количество ≥ 3, но не более 10. Выписать эти маршруты для какой-либо из выделенных пар. В описании маршрутов указывать вершины и рёбра, входящие в него. 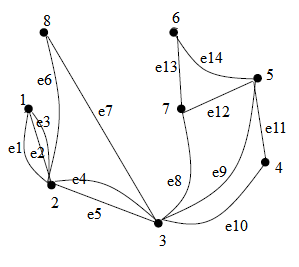 Решение Составляем матрицу смежности  Найдем матрицу А4, в которой каждый элемент равен количеству маршрутов длины 4  В графе 5 пар вершин, для которых количество маршрутов длины 4 не менее 3, но не более 10. Выпишем маршруты для пары (6,8): 1) {e14;e11;e10;e7} 2) {e14;e12;e8;e7} 3) {e13;e12;e9;e7} 4) {e13;e8;e4;e6} 5) {e13;e8;e5;e6} 6) {e14;e9;e4;e6} 7) {e14;e9;e5;e6} Задание 4. Построить матрицу метрики графа  Решение Расстоянием  Задание 5. С помощью алгоритма Магу—Вейсмана выполнить правильную раскраску вершин графа с минимальным количеством цветов.  Решение Составим произведение ПG и найдем семейство МВУП:  Получаем семейство МВУП: F1 ={X2,X4,X7 } F2={X1,X4,X7,X8 } F3={X2,X5} F4={X1,X5,X8} F5={X2,X4,X6} F6={X1,X3,X6} F7={X1,X4,X6,X8} F={F1,F2,F3,F4,F5,F6,F7} Нет ни одной пары FiFj, которые покрывают все вершины графа, но есть тройка, например F2F3F6. Значит, для раскраски требуется минимум 3 цвета. Один из вариантов раскраски графа: F2F3F6={X1,X4,X7,X8 }{X2,X5}{X3,X6} 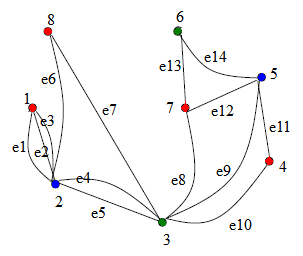 Задание 6. Определить число вершинного покрытия графа. 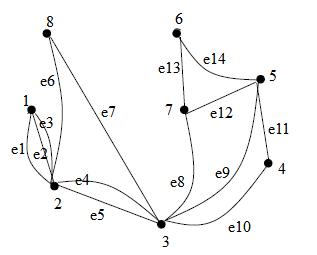 Решение Выберем ребро e5=(2,3) S={2,3}, удаляем ребра, инцидентные этим вершинам. 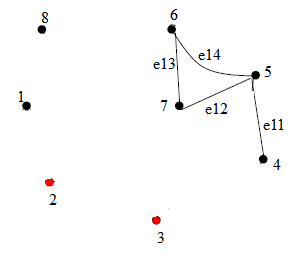 Выберем ребро e12=(5,7). S={2,3,5,7}, удаляем инцидентные ребра 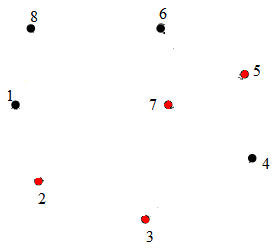 Получаем S={2,3,5,7}, следовательно, число вершинного покрытия равно 4 Задание 7. Определить содержит ли граф (рис. 1) эйлерову цепь или эйлеров цикл?  Найдем степени вершин графа:
В графе ровно две вершины нечетной степени, это означает, что в нем нет эйлерова цикла, но есть эйлерова цепь, например: e1→e2→e3→e4→e5→e6→e7→e8→e12→e9→e10→e11→e14→e13 Задание 8 Аналитическим способом определить число компонент связности графа  Построим граф 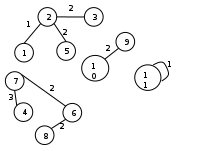 Найдем количество компонент связности K методом поиска в глубину. К=1 Пусть 1 - начальная вершина Из вершины 1 можем попасть в вершину 2. Из вершины 2 можем попасть в вершину 3. У вершины 3 нет смежных непосещенных вершин, вернемся к вершине 2. Из вершины 2 можем попасть в вершину 5. У вершины 5 нет смежных непосещенных вершин, вернемся к вершине 2. У вершины 2 нет смежных непосещенных вершин, вернемся к вершине 1. У вершины 1 нет смежных непосещенных вершин. Компонента связности найдена. К=2 Пусть 4 - начальная вершина Из вершины 4 можем попасть в вершину 7. Из вершины 7 можем попасть в вершину 6. Из вершины 6 можем попасть в вершину 8. У вершины 8 нет смежных непосещенных вершин, вернемся к вершине 6. У вершины 6 нет смежных непосещенных вершин, вернемся к вершине 7. У вершины 7 нет смежных непосещенных вершин, вернемся к вершине 4. У вершины 4 нет смежных непосещенных вершин. Компонента связности найдена. К=3 Пусть 9 - начальная вершина Из вершины 9 можем попасть в вершину 10. У вершины 10 нет смежных непосещенных вершин, вернемся к вершине 9. У вершины 9 нет смежных непосещенных вершин. Компонента связности найдена. К=4 Пусть 11 - начальная вершина У вершины 11 нет смежных непосещенных вершин. Компонента связности найдена. Все вершины графа посещены, граф содержит 4 компоненты связности Заключение При выполнении данной лабораторной работы мной были изучены: Принцип построения графа по матрицам смежности и инцидентности. Алгоритмы обхода графа «в глубину» и «в ширину». Принцип составления матрицы метрики графа Принцип поиска количества маршрутов определенной длины в графе. Алгоритм раскраски графа Магу—Вейсмана Алгоритм нахождения вершинного покрытия графа Принцип определения наличия в графе Эйлерового цикла и Эйлеровой цепи. Алгоритм нахождения компонент связности графа При выполнении лабораторной работы мной были получены практические навыки применения этих методов при решении задач. Список использованной литературы Жигалова Е.Ф. Дискретная математика : учебное пособие / Е.Ф.Жигалова. — Томск : Эль Контент, 2014. — 98 с. Зыков А.А. Основы теории графов. - М.:Наука, 1987, 384 с. Новиков Ф. А. Н73 Дискретная математика для программистов: Учебник для вузов. 3-е изд. — СПб.: Питер, 2009. — 384 е.: ил. — (Серия «Учебник для вузов») |
