Задачи линейного программирования в экономике. Составление экономико-математической модели задачи линейного программирования. Лр1. Лабораторная работа 1 по дисциплине Математические методы и модели поддержки принятия решений на тему
 Скачать 27.67 Kb. Скачать 27.67 Kb.
|
Институт передовых информационных технологий Лабораторная работа №1 по дисциплине Математические методы и модели поддержки принятия решений на тему: Задачи линейного программирования в экономике. Составление экономико-математической модели задачи линейного программирования Выполнил: Камынин В.А. студент II курса группы 1581011 Проверил: ст. преподаватель Басалов Ю.А. Тула 2022 г. ЦЕЛЬ РАБОТЫ: Приобретение навыков составления экономико-математической модели задач линейного программирования. Вариант 3 «Princetown PaintsLtd» выпускает два основных типа румян – перламутровые и матовые – с использованием одинаковых смесеобразующих машин и видов работ. Главному бухгалтеру фирмы было поручено разработать для компании план производства на неделю. Информация о ценах продаж и стоимости 100 л товара приведена в таблице (ф. ст.). Таблица – 1 Данные задачи
Стоимость 1 чел.-ч составляет 3 ф. ст. а стоимость 1 ч приготовления смеси – 4 ф. ст. Фонд рабочего времени ограничен 8000 чел.-ч. в неделю, а ограничение на фонд работы смесеобразующих машин равно 5900 ч в неделю. В соответствии с контрактными соглашениями компания должна производить 25000 л матовых румян в неделю. Максимальный спрос на перламутровые румяна – 29000 л в неделю. Требуется сформулировать математическую модель задачи, позволяющую определить объемы производства матовых и перламутровых румян в неделю, при которых достигается максимальное значение получаемой за неделю прибыли. Решение Составим экономико-математическую модель задачи. Обозначим: x1 – объём матовых румян, л.; x2 – объём перламутровых румян, л. Доход от реализации матовых румян составляет 110x1, а от реализации перламутровых румян 126x2, на 100 л. Прибыль — это разница между расходами и доходами. Расходы по издержкам по статьям затрат: «Стоимость сырья» и «Другие издержки» матовых румян составляют (20+10)x1, а издержки перламутровых румян (25+15)x2, на 100 л. x1 ≥25000 ограничение по минимальному объёму матовых румян x2 ≤29000 ограничение по максимальному объёму перламутровых румян x1 ≥0; x2 ≥0; ограничения по смыслу задачи (24/3)x1+(36/3)x2 ≤8000 ограничение по фонду рабочего времени, ч на 100 л. Или 8x1+12x2 ≤8000, или 2x1+3x2 ≤2000 (35/4)x1+(20/4)x2 ≤5900 ограничение по фонду работы смесеобразующих машин, ч. на 100 л. Или 8,75x1+5x2 ≤5900 Прибыль: Z=110x1+126x2 – 30x1 – 40x2 или Z=80x1+86x2 Таким образом, экономико-математическая модель задачи примет вид: Z=80x1+86x2 max при ограничениях 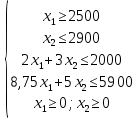 | |||||||||||||||||||||||||

