ИССЛЕДОВАНИЕ ПРОСТЕЙШИХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ. Лабораторная работа 1 по курсу электроника 2 исследование простейших электрических цепей Вариант 1
 Скачать 343.71 Kb. Скачать 343.71 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Инженерная школа неразрушающего контроля и безопасности Направление 12.03.01 Приборостроение Отделение контроля и диагностики ЛАБОРАТОРНАЯ РАБОТА №1 по курсу «электроника 1.2» «ИССЛЕДОВАНИЕ ПРОСТЕЙШИХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ» Вариант 1 Выполнил: студент гр.1Б81 Айсагалиева А.А Принял: доцент ОЭИ Силушкин С.В. Томск – 2022 Цель работыЗнакомство со средой Multisim. Исследование свойств простейших RC-цепей, широко использующихся в электронике при прохождении гармонических сигналов. Программа работыИзучить описание среды схемотехнического моделирования и анализа электрических схем Multisim; Выполнить предварительные выводы основных соотношений и расчеты; Провести исследование резистивного делителя напряжения; Провести исследование работы простейших RC-цепей; Сделать необходимые выводы. Ход работыВыполнение предварительного задания Прежде чем приступить к выполнению данной работы, было изучено описание среды моделирования и анализа электрических схем Multisim. Помимо прочего пришлось повторить такие темы курса как "Электрические сигналы", "Резистивный делитель", "Простейшие фильтры". Для анализа схем из данной работы был рассчитан коэффициент деления резистивного делителя для моего варианта: 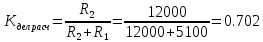 Также для исследуемых RC-цепей были получены аналитические выражения для АЧХ, ФЧХ, граничной частоты и частоты, на которой коэффициент передачи по напряжению будет максимален (для полосового фильтра). В выводе условимся, что все сопротивления равны между собой и все емкости тоже равны между собой. ФНЧ 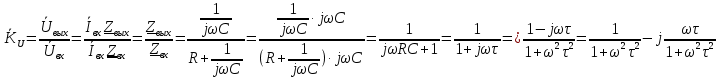 Выражение для АЧХ: 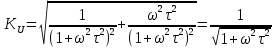 Выражение для ФЧХ: 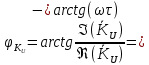 Вывод для граничной частоты: 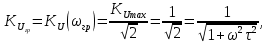 отсюда 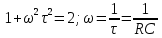 . .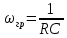 ФВЧ 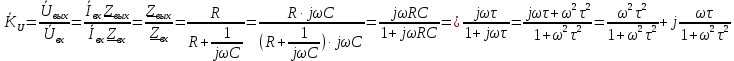 Выражение для АЧХ: 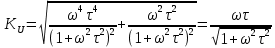 Выражение для ФЧХ: 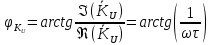 Вывод для граничной частоты: 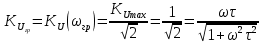 отсюда 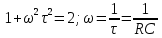 . .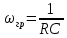 Полосовой фильтр 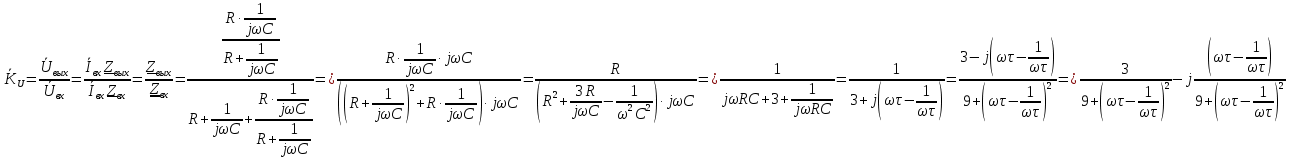 Выражение для АЧХ: 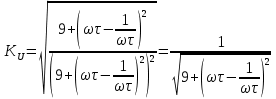 Выражение для ФЧХ: 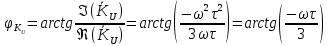 Получение выражения для частоты, при которой коэффициент передачи максимален: 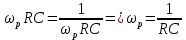 Здесь необходимо учесть, что максимальная величина модуля коэффициента передачи наблюдается при 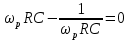 . .Рассчитаем характерные параметры исследуемых RC-цепей: 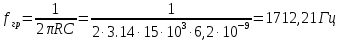 Исследование резистивного делителя напряжения Делитель без нагрузкиНарисуем схему резистивного делителя без нагрузки. Номиналы сопротивлений резисторов заданы в соответствии с предварительным заданием. На вход делителя подключен источник постоянного напряжения величиной 12В. Для простоты измерения параметров в ключевых точках установлены маркеры тока и напряжения. 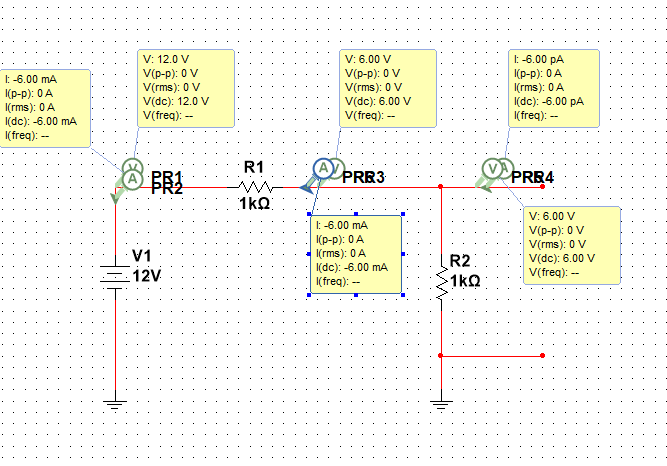 Рисунок 1 – Схема резистивного делителя без нагрузки Зафиксируем основные значения тока и напряжения: 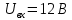 ; ;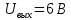 ; ;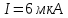 . .Используя значения входного и выходного напряжений, определим экспериментальное значение коэффициента деления схемы и сравним его с расчетным значением: 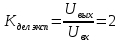 Можно увидеть, что экспериментальное и расчетное значения коэффициента передачи равны между собой. Значит, что все значения сняты верно. Рассчитаем мощности, рассеиваемые на резисторах: 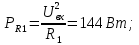 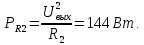 Напряжение на выходе делителя меньше, чем на входе, из-за наличия в схеме делителя сопротивлений, которые приводят к падению напряжения на выходе (согласно закона Ома). За счет всех этих падений и уменьшается значение выходного напряжения. Делитель с нагрузкойК выходу схемы, рассмотренной ранее, подключим сопротивление нагрузки. Как и в предыдущем случае для простоты измерения параметров в ключевые точки схемы поставим установим маркеры тока и напряжения. Номиналы сопротивлений резисторов заданы в соответствии с предварительным заданием; сопротивление 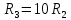 . .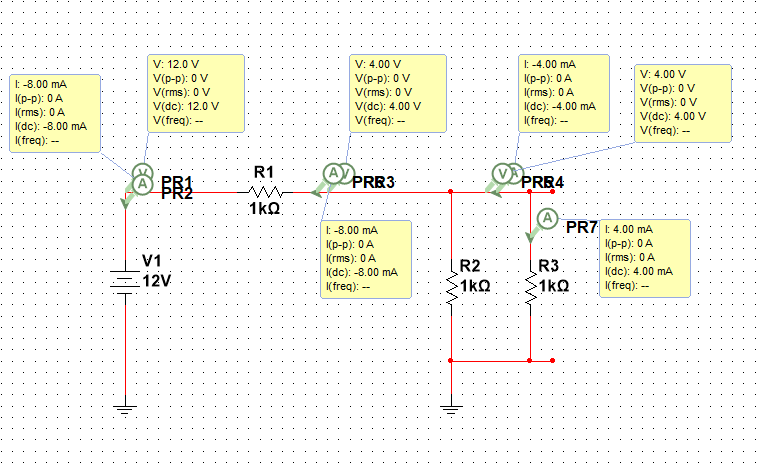 Рисунок 2 – Схема резистивного делителя с нагрузкой Зафиксируем основные значения тока и напряжения: 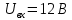 ; ;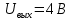 ; ;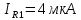 ; ;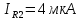 ; ;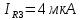 . .Используя значения входного и выходного напряжений, определим экспериментальное значение коэффициента деления схемы и сравним его со значением без нагрузки: 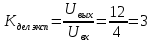 Значение коэффициента деления с нагрузкой и без нагрузки заметно отличаются друг от друга. Это связано с появлением нагрузки (в лице дополнительного сопротивления), что приводит к ещё большему падению входного напряжения, что, в свою очередь, приводит к уменьшению напряжения на выходе. Таким образом, можно сделать вывод, что сопротивление нагрузки неминуемо понижает коэффициент деления. Резистивный делитель с нагрузкой и источником гармонического напряженияЗа основу возьмем схему из предыдущего пункта и заменим в ней источник постоянного напряжения на источник гармонического напряжения. Для наблюдения сфазированных осциллограмм подключен осциллограф. 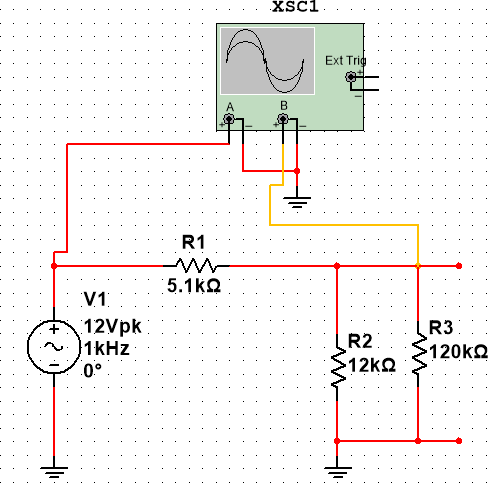 Рисунок 3 – Схема резистивного делителя с подключением осциллографа Считаем осциллограмму. Для наглядности установим несколько периодов сигнала на экране, удобные для наблюдения. Используя метки осциллографа измеряем амплитуду и период входного и выходного сигналов. 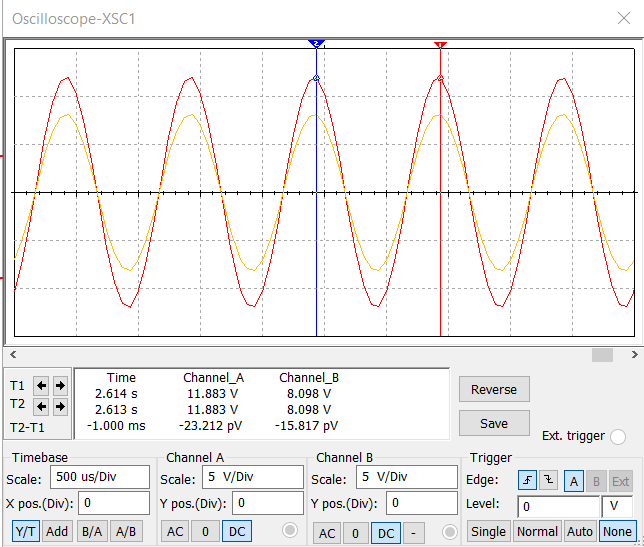 Рисунок 4 – Осциллограмма резистивного делителя Амплитуды входного и выходного сигналов: 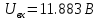 , , 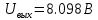 Период Т: 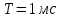 Определим экспериментальное значение коэффициента деления схемы и сравним его со значением из предыдущего пункта. Здесь необходимо помнить, что в цепи течет переменный ток, а значения, снятые на осциллографе, являются амплитудными. А для расчета необходимо использовать действующие значения напряжений. С учетом этого коэффициент деления равен: 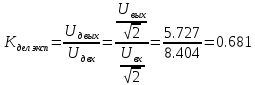 Значения коэффициентов деления, полученные в этом и предыдущем пунктах, абсолютно идентичны. Это связано с источником напряжения для схемы в этом пункте: он способен выдавать только амплитудные значения, которые практически неотличимы от значений, выдаваемых источником постоянного напряжения. Рассчитаем мощности, рассеиваемые на резисторах схемы: 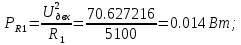 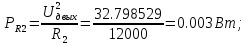 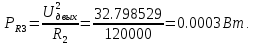 Полученные мощности сильно отличаются от полученных ранее. Это связано с тем, что при расчете мощностей используются действующие значения напряжений, которые ниже амплитудных. Таким образом, уменьшение напряжения приводит к уменьшению мощности, рассеиваемой на резисторах. Исследование простейших RC-цепей Фильтр низких частотИзобразим схему фильтра низких частот. Номиналы сопротивлений резисторов и емкостей конденсаторов заданы в соответствии с предварительным заданием. Ко входу схемы подключен источник гармонического сигнала с параметрами 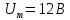 , и частотой, равной граничной. , и частотой, равной граничной.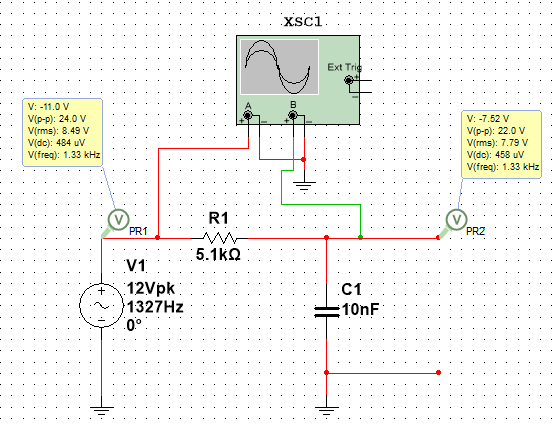 Рисунок 5 – Схема фильтра низких частот с подключением осциллографа Используя возможности осциллографа, определим входное и выходное напряжения. 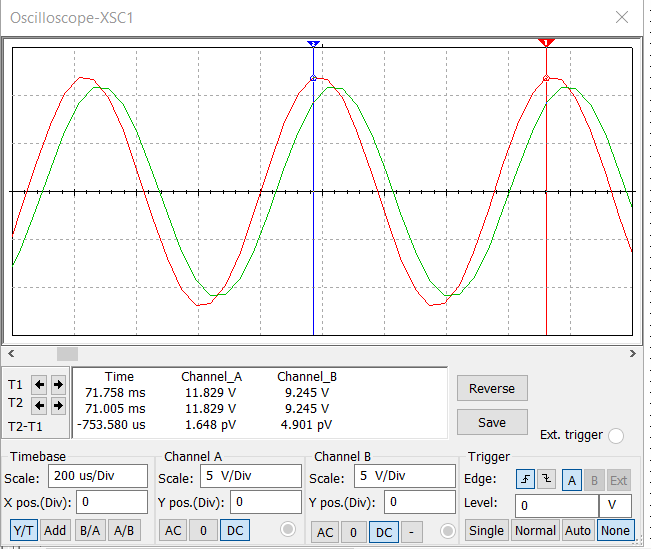 Рисунок 6 – Входной и выходной сигналы на экране осциллографа С помощью маркеров определим напряжения входного и выходного напряжений: 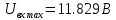 , , 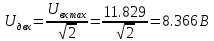 ; ;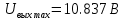 , , 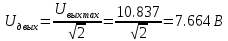 . .Рассчитаем коэффициент передачи схемы: 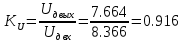 Далее можем рассчитать фазовый сдвиг. Расчет будем осуществлять осциллографическим методом с применением формулы: 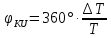 Сначала определим период: 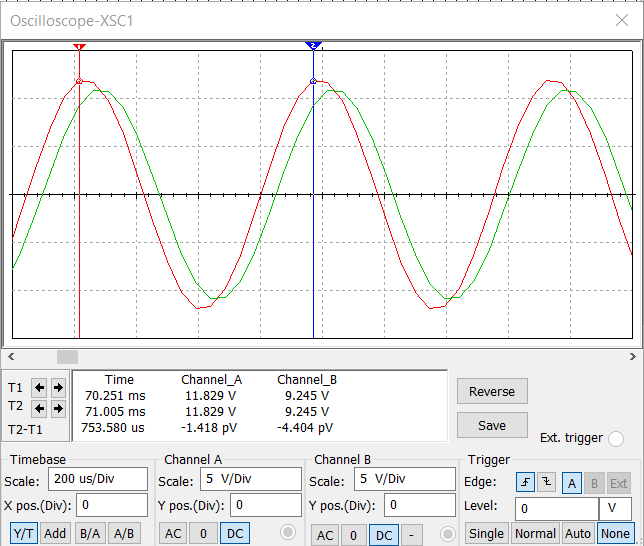 Рисунок 7 – Определение периода с помощью осциллограммы Видим, что период 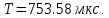 Теперь определяем 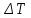 : :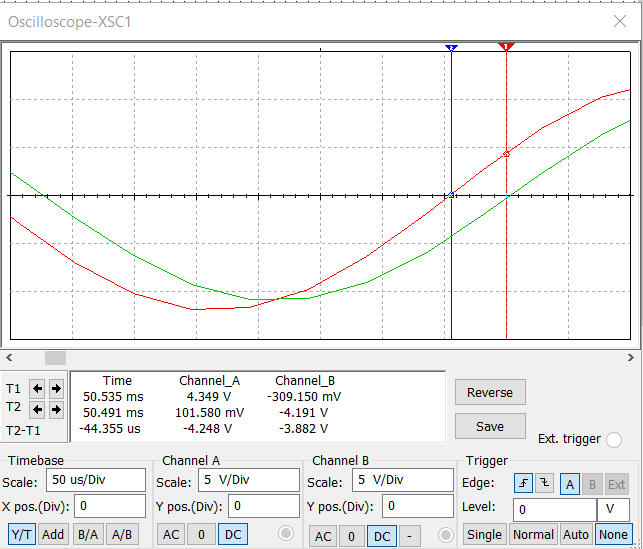 Рисунок 8 – Определение величины 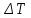 с помощью осциллограммы с помощью осциллограммыВидим, что 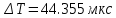 Таким образом, фазовый сдвиг равен: 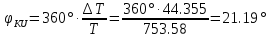 Можно сделать вывод, что выходной сигнал опережает входной на 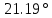 . .Анализ RC-цепи при 0.5 fгрВ этом случае частота источника равна 664 Гц. В остальном все действия абсолютно идентичны действиям из предыдущего пункта. Определяем с помощью осциллографа максимальные значения напряжений на входе и выходе цепи. Не забываем выражать через них действующие значения. 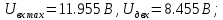 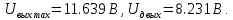 Считаем коэффициент передачи: 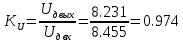 Определяем фазовый сдвиг: 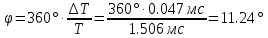 Анализ RC-цепи при 1.5 fгрВ этом случае частота источника равна 1991 Гц. В остальном все действия абсолютно идентичны действиям из предыдущего пункта. Определяем с помощью осциллографа максимальные значения напряжений на входе и выходе цепи. Не забываем выражать через них действующие значения. 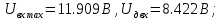 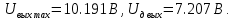 Считаем коэффициент передачи: 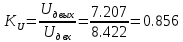 Определяем фазовый сдвиг: 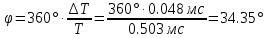 Определив значения фазового сдвига и коэффициентов передачи при разных частотах источника, можно сделать вывод, что с ростом частоты источника уменьшается значение коэффициентов передачи из-за уменьшения значения выходного напряжения. Значение же фазового сдвига, наоборот, увеличивается. Снимем АЧХ и ФЧХ фильтра, установив пробники на вход и выход схемы. Графики предоставлены в отчете. На характеристики нанесем полосы пропускания и подавления.   Полоса подавления Полоса пропускания 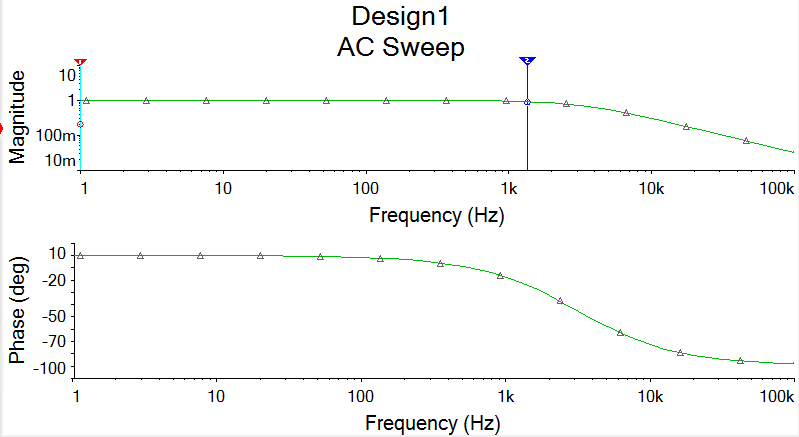 Рисунок 9 – АЧХ и ФЧХ фильтра низких частот с полосами пропускания и подавления Фильтр высоких частотИзобразим схему фильтра высоких частот. Номиналы сопротивлений резисторов и емкостей конденсаторов заданы в соответствии с предварительным заданием. Ко входу схемы подключен источник гармонического сигнала с параметрами 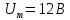 , и частотой, равной граничной. , и частотой, равной граничной.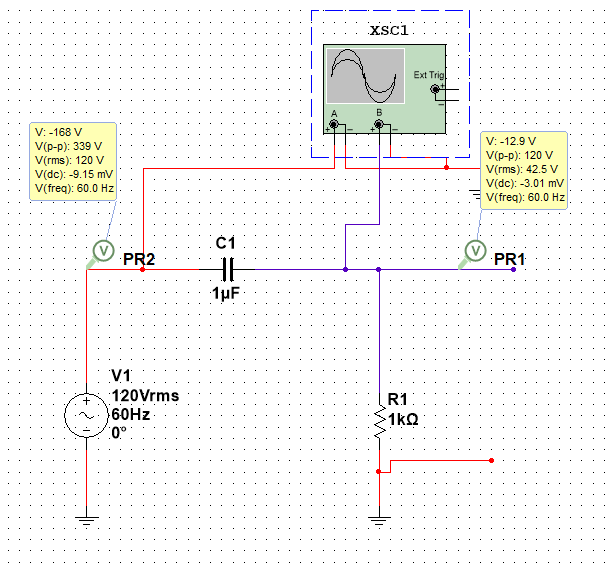 Рисунок 10 – Схема фильтра высоких частот с подключением осциллографа Используя возможности осциллографа, определим входное и выходное напряжения. 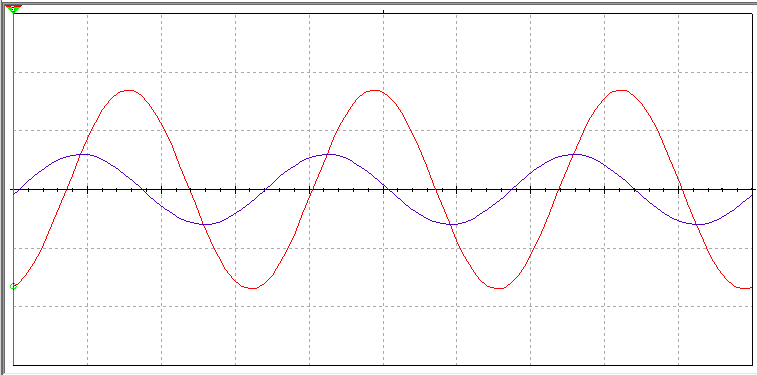 Рисунок 11 – Входной и выходной сигналы на экране осциллографа С помощью маркеров определим напряжения входного и выходного напряжений, а также период Т: 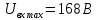 , , 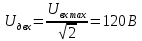 ; ;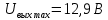 , , 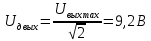 . .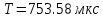 . .  Полоса пропускания Полоса подавления 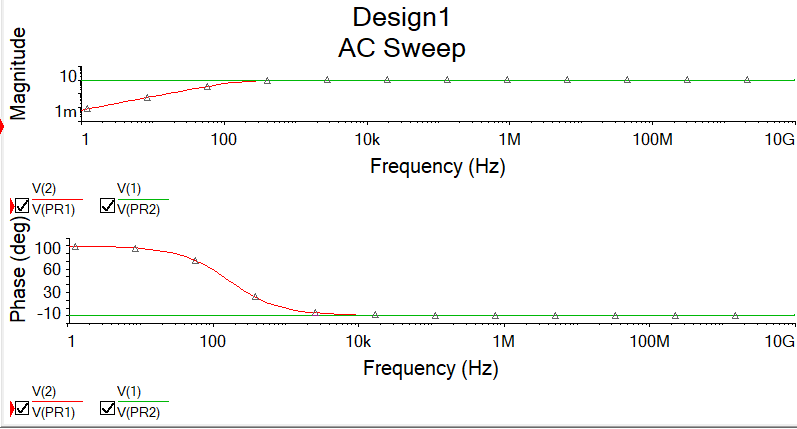 Рисунок 12 – АЧХ и ФЧХ фильтра высоких частот с полосами пропускания и подавления Полосовой фильтрИзобразим схему полосового филльтра. Номиналы сопротивлений резисторов и емкостей конденсаторов заданы в соответствии с предварительным заданием. Ко входу схемы подключен источник гармонического сигнала с параметрами 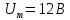 , и частотой, равной граничной. , и частотой, равной граничной.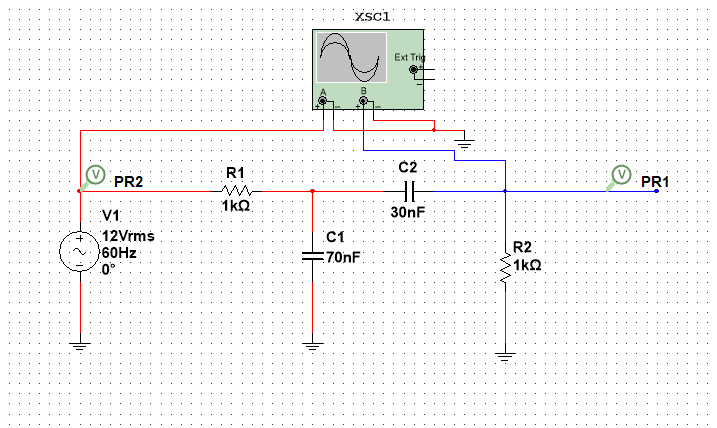 Рисунок 13 – Схема полосового фильтра с подключением осциллографа Используя возможности осциллографа, определим входное и выходное напряжения. 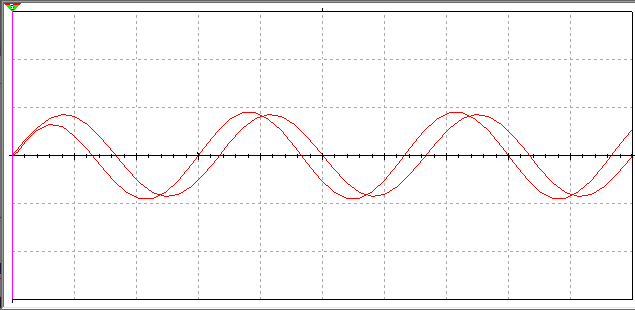   Полоса Рисунок 14 – Входной и выходной сигналы на экране осциллографа ВыводВ ходе выполнения данной лабораторной работы мы познакомились со средой Multisim, а также спроектировали цепи. Для каждой из цепей сделали расчеты и построили АЧХ и ФЧХ. |
