Содержание
Лабораторная работа №1. «Расчет гидравлического режима совместной работы участка нефтепровода и нефтеперекачивающей станции» 2
Теоретическое введение 2
Задания лабораторной работы 12
Работа с программой «Режим» 14
Порядок выполнения работы 19
Лабораторная работа №2. «Расчет гидравлического режима совместной работы НПС и сложного участка нефтепровода (с вставками или лупингом)» 24
Теоретическое введение 24
Задания лабораторной работы 29
Работа с программой «Комплекс» 31
Порядок выполнения работы 37
Лабораторная работа №3. «Расчет гидравлического режима работы участка нефтепровода с промежуточными нефтеперекачивающими станциями» 41
Теоретическое введение 41
Задания лабораторной работы 45
Работа с программой «Транзит» 48
Порядок выполнения работы 53
Лабораторная работа №4. «Расчет гидравлического удара на участке трубопровода» 57
Теоретическое введение 57
Задания лабораторной работы 78
Работа с программой «Гидроудар» 80
Порядок выполнения работы 87
Лабораторная работа №5. «Расчет смесеобразования при последовательной перекачке нефтепродуктов» 90
Теоретическое введение 90
Задания лабораторной работы 96
Работа с программой «Смесь» 97
Порядок выполнения работы 100
Лабораторная работа №6. «Термогидравлический расчет участка трубопровода при перекачке нефтей и нефтепродуктов с подогревом» 102
Теоретическое введение 102
Задания лабораторной работы 107
Работа с программой «Термика» 109
Порядок выполнения работы 115
Рекомендуемая литература 119
Теоретическое введение
Уравнение Бернулли для участка нефтепровода. В основе гидравлических расчетов участка трубопровода, по которому осуществляется перекачка нефти (см. рис.1), лежит хорошо известное уравнение Бернулли:
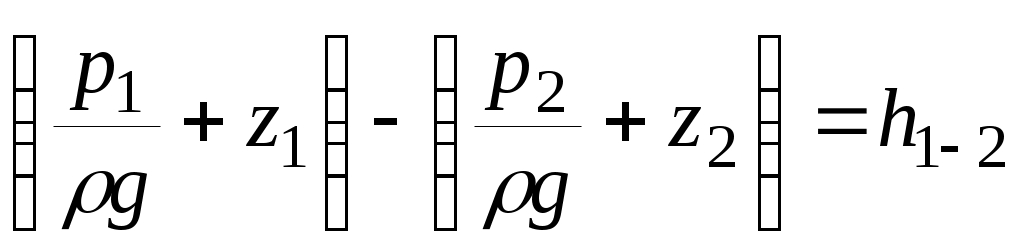 , (1.1) , (1.1)
в котором p1 и p2 – давления в сечениях x1 и x2 нефтепровода, соответственно; z1 и z2 – высотные отметки этих сечений, ρ – плотность нефти, g – ускорение свободного падения, а 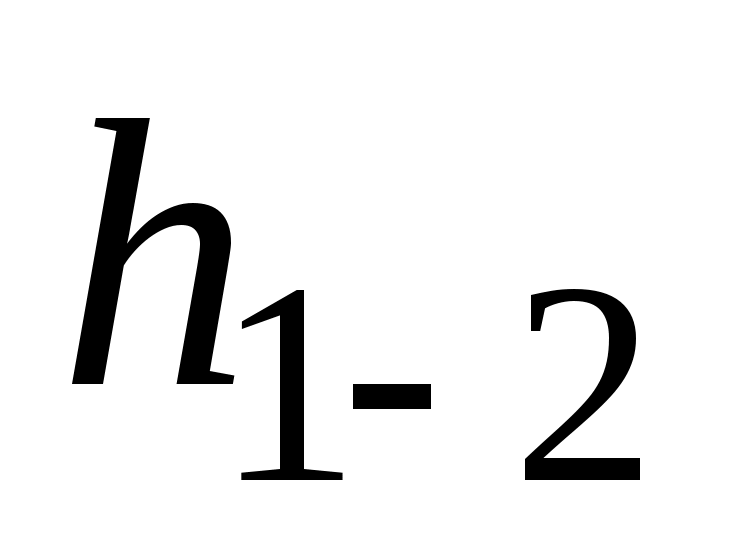 – потери напора на участке [x1, x2] трубопровода. Отношение – потери напора на участке [x1, x2] трубопровода. Отношение 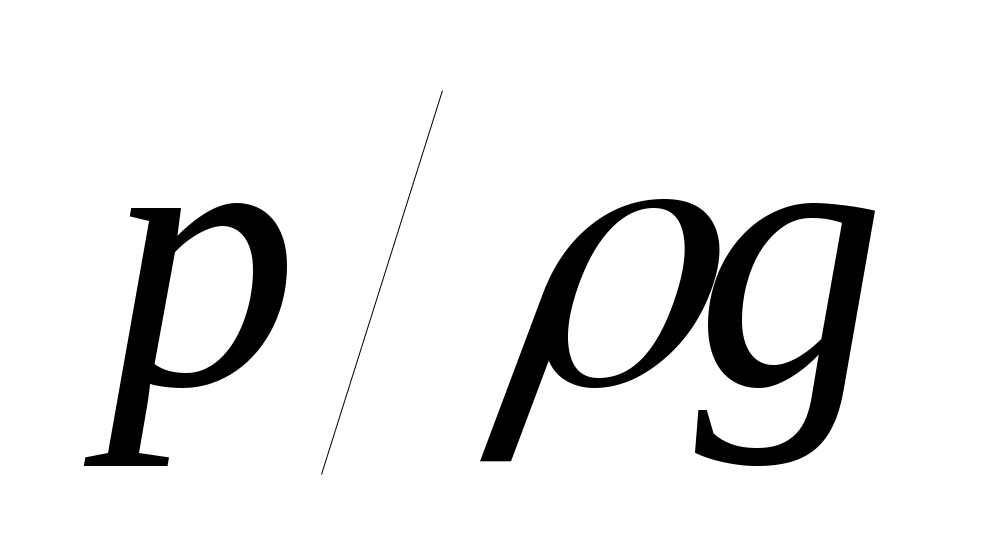 называется пьезометрическим напором, а величина называется пьезометрическим напором, а величина  – геометрическим напором в сечении – геометрическим напором в сечении 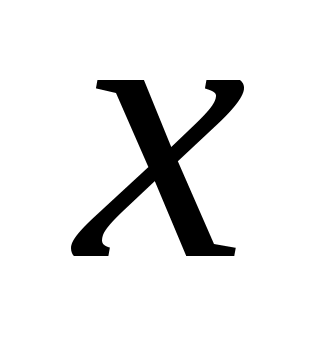 трубопровода. Обе величины измеряются в метрах. трубопровода. Обе величины измеряются в метрах.
Потери напора 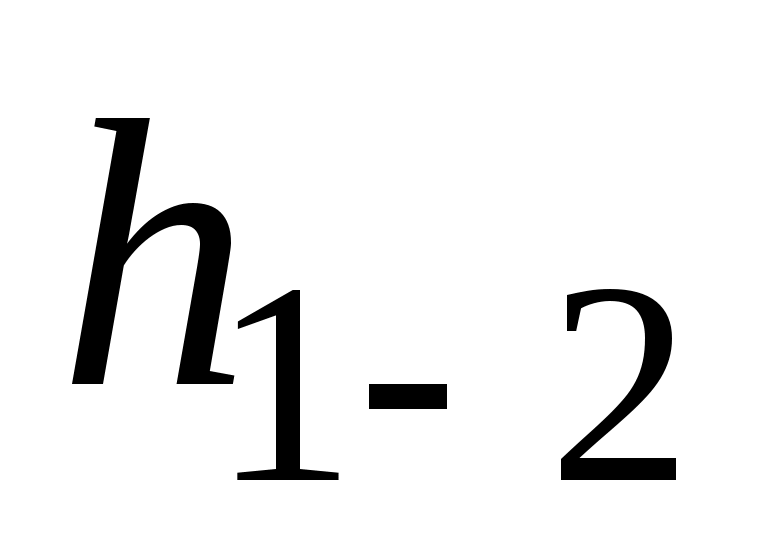 на участке[x1, x2] нефтепровода состоят из двух частей: на участке[x1, x2] нефтепровода состоят из двух частей:
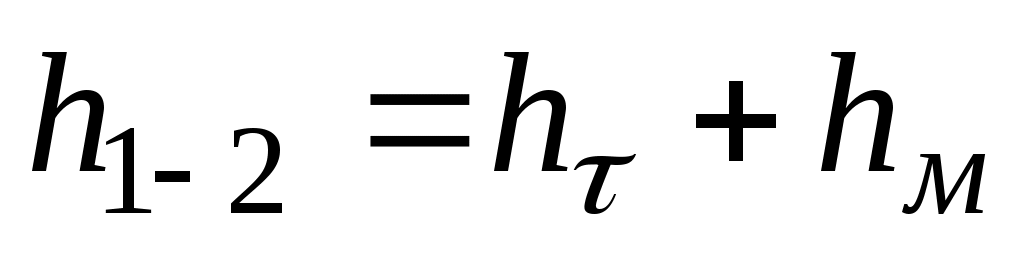 . (1.2) . (1.2)
Первое слагаемое называется потерей напора на трение. Оно выражает потери механической энергии за счет сил внутреннего трения слоев вязкой нефти друг о друга. Второе слагаемое называется потерей напора на преодоление местных сопротивлений (сужений, поворотов, задвижек и т.п.). [1, 4, 6]
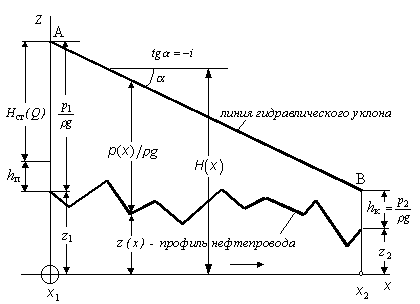
Рис.1. К гидравлическому расчету участка нефтепровода
Потери напора 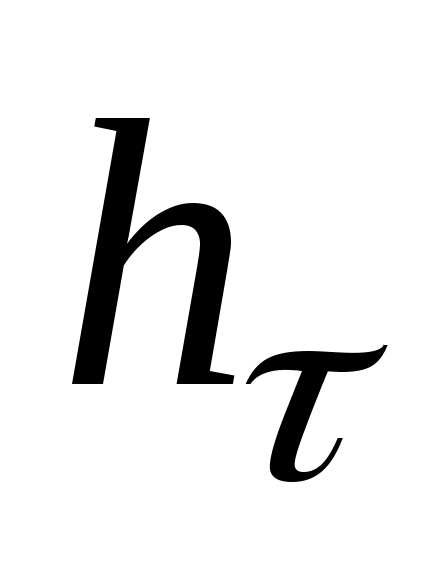 (м) на трение рассчитывают по формуле (м) на трение рассчитывают по формуле
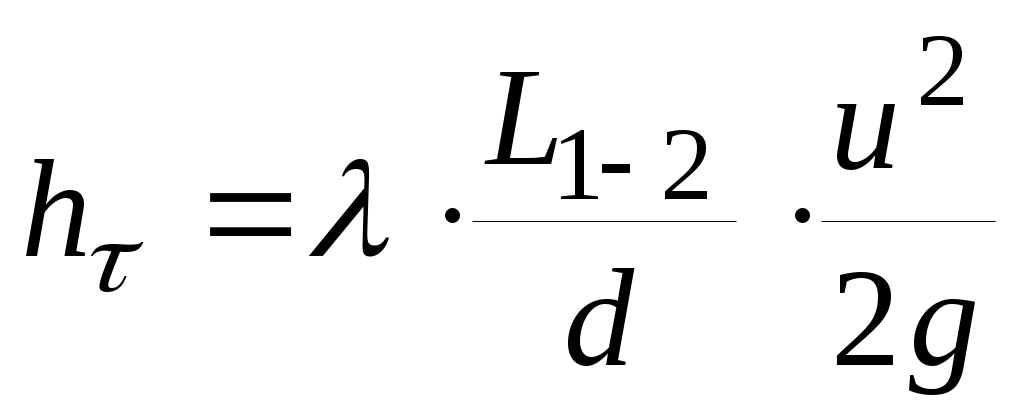 , (1.3) , (1.3)
называемой формулой Дарси-Вейсбаха. В этой формуле 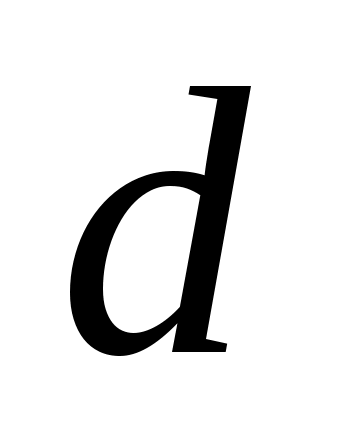 – внутренний диаметр трубопровода; – внутренний диаметр трубопровода;  – средняя по сечению скорость перекачки ( – средняя по сечению скорость перекачки (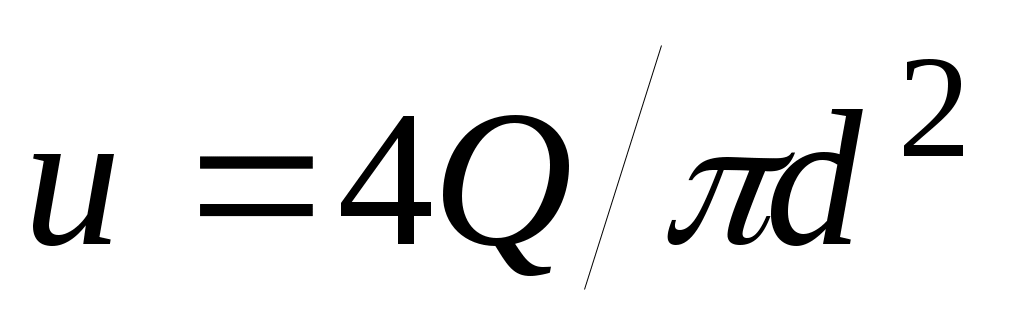 , где Q – объемный расход перекачки); , где Q – объемный расход перекачки);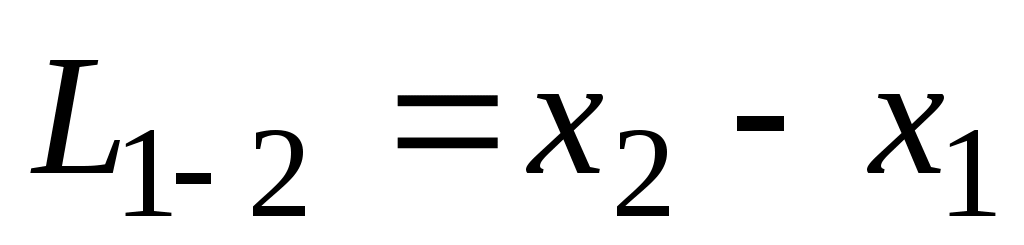 – длина участка трубопровода между рассматриваемыми сечениямиx1 и x2; – длина участка трубопровода между рассматриваемыми сечениямиx1 и x2; 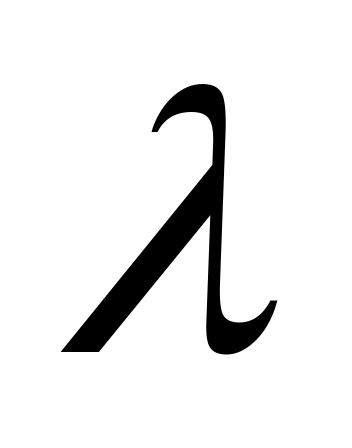 – коэффициент гидравлического сопротивления. – коэффициент гидравлического сопротивления.
Потери напора 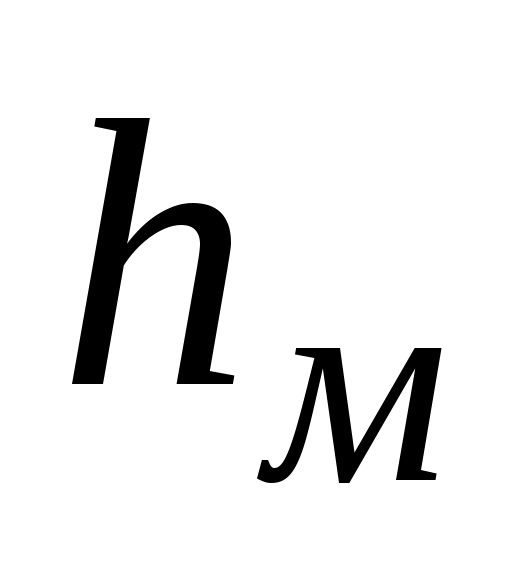 (м) на преодоление местных сопротивлений рассчитывают по формуле (м) на преодоление местных сопротивлений рассчитывают по формуле
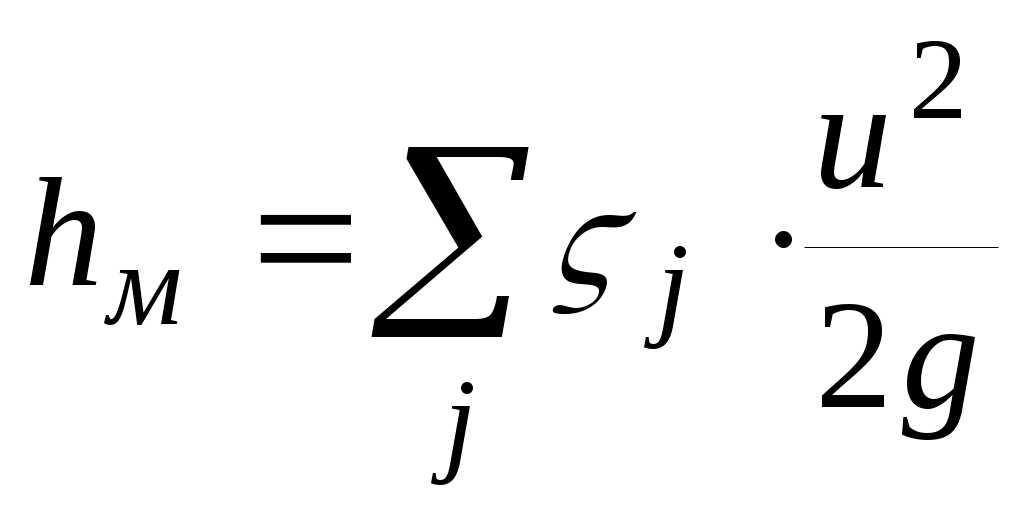 , (1.4) , (1.4)
в которой  - коэффициенты местных сопротивлений, а суммирование осуществляется по всем сопротивлениям, имеющимся на участке[x1, x2]. - коэффициенты местных сопротивлений, а суммирование осуществляется по всем сопротивлениям, имеющимся на участке[x1, x2].
Иногда наличие местных сопротивлений в магистральном нефтепроводе учитывают огрубленно, полагая, что потери напора на местных сопротивлениях составляют примерно 2% от потерь напора на трение, т.е. принимают, что 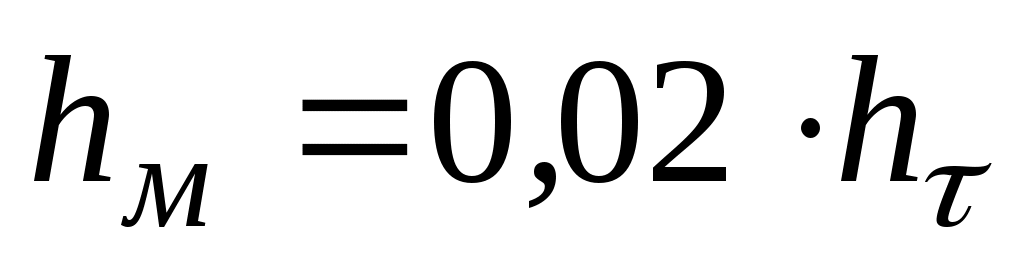 . В этом случае полные потери напора . В этом случае полные потери напора 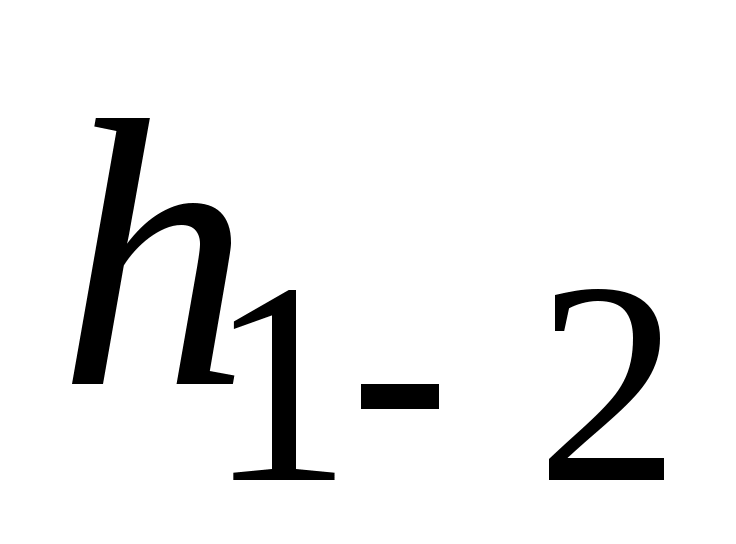 на участке нефтепровода между сечениями на участке нефтепровода между сечениями 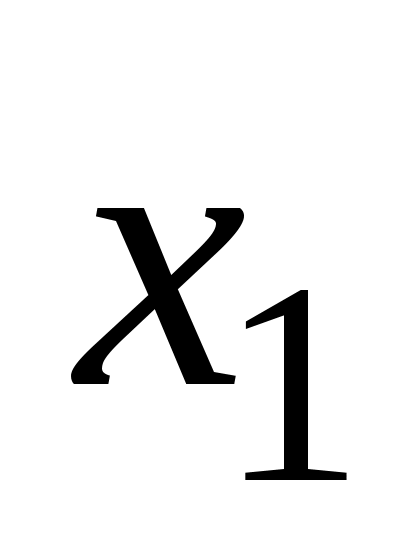 и и 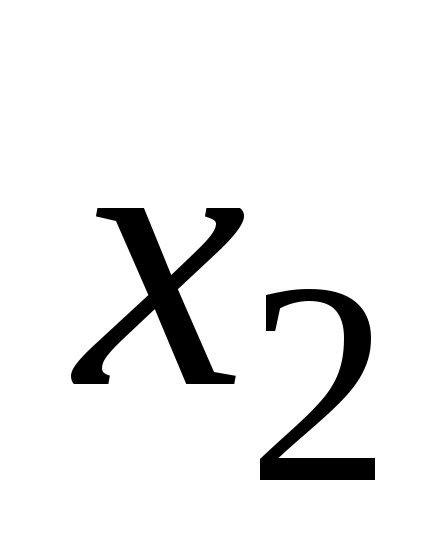 вычисляются по формуле: вычисляются по формуле:
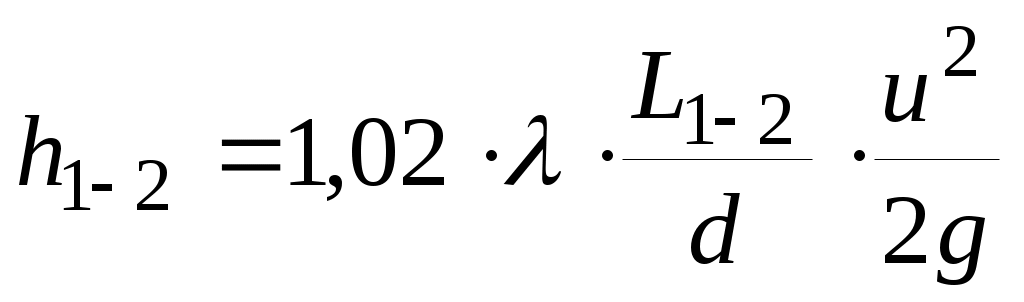 . (1.5) . (1.5)
Если учесть, что коэффициент λ гидравлического сопротивления есть функция от числа Рейнольдса 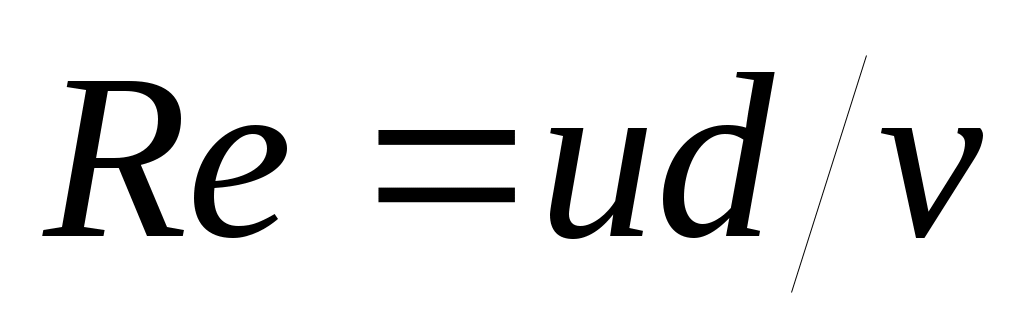 (ν – кинематическая вязкость нефти) и относительной шероховатости ε внутренней поверхности труб: (ν – кинематическая вязкость нефти) и относительной шероховатости ε внутренней поверхности труб: 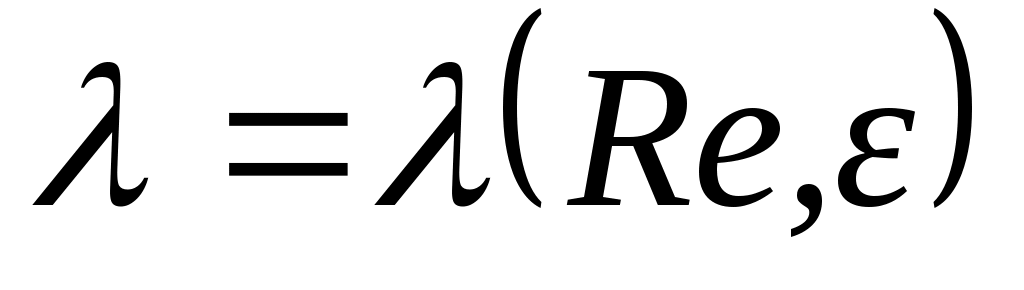 . А значит, коэффициент λ зависит (через число Re) от скорости перекачки и, следовательно, от расхода нефти. Уравнение Бернулли (1.1) с учетом формул (1.2) – (1.4), записанное в форме . А значит, коэффициент λ зависит (через число Re) от скорости перекачки и, следовательно, от расхода нефти. Уравнение Бернулли (1.1) с учетом формул (1.2) – (1.4), записанное в форме
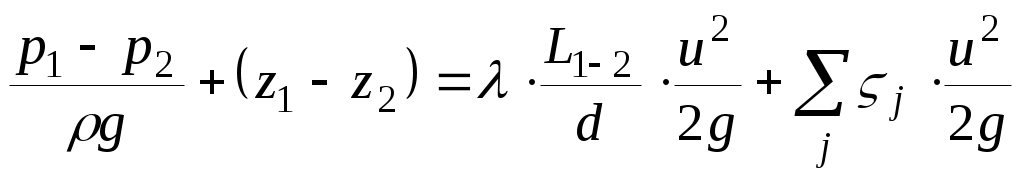 , (1.6) , (1.6)
является соотношением, связывающим давления в сечениях x1 и x2 со скоростью перекачки, а, следовательно, и с ее расходом 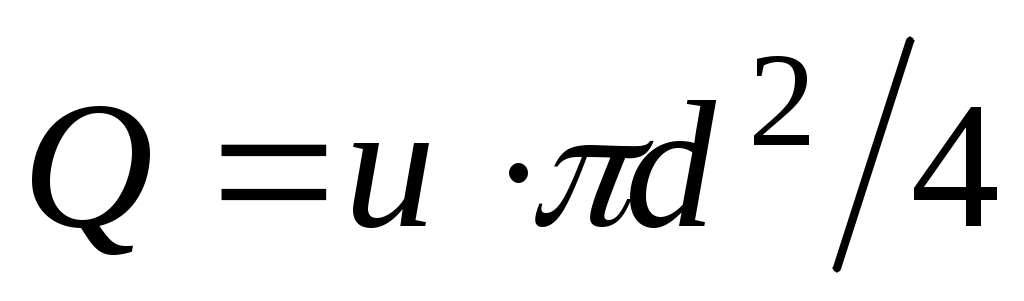 . .
Коэффициент гидравлического сопротивления. Для расчета коэффициента λ гидравлического сопротивления можно использовать следующие формулы [4, 6].
Если число Рейнольдса 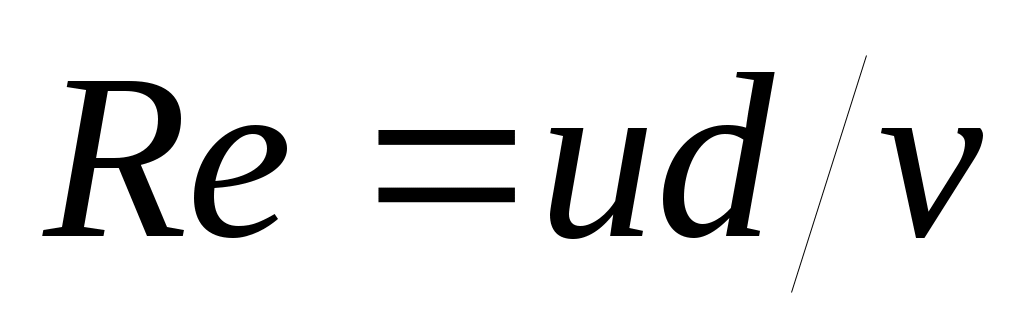 <2320, то течение нефти ламинарное. Для него <2320, то течение нефти ламинарное. Для него
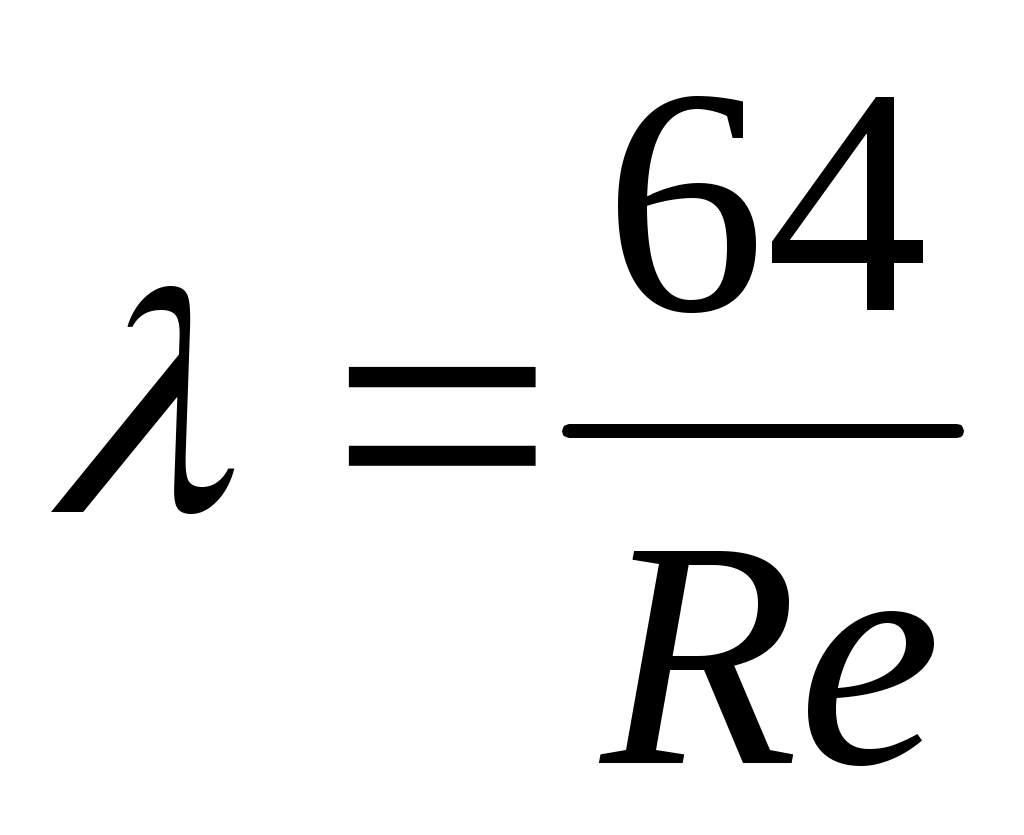 (формула Стокса). (1.7) (формула Стокса). (1.7)
Ламинарное течение может реализоваться для высоковязких нефтей, течение которых характеризуется относительно небольшими числами Рейнольдса.
Если 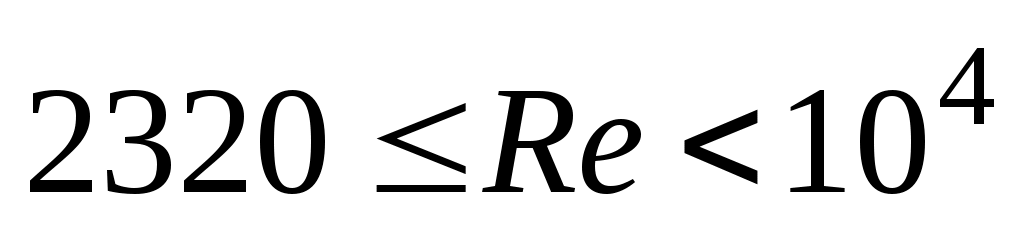 , то режим течения нефти «переходный турбулентный» и , то режим течения нефти «переходный турбулентный» и
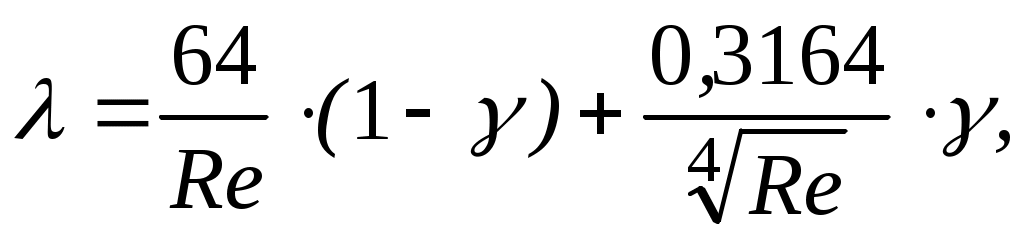 (1.8) (1.8)
где 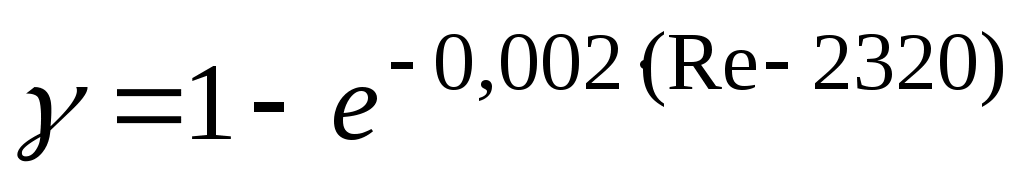 – так называемый коэффициент перемежаемости. – так называемый коэффициент перемежаемости.
Если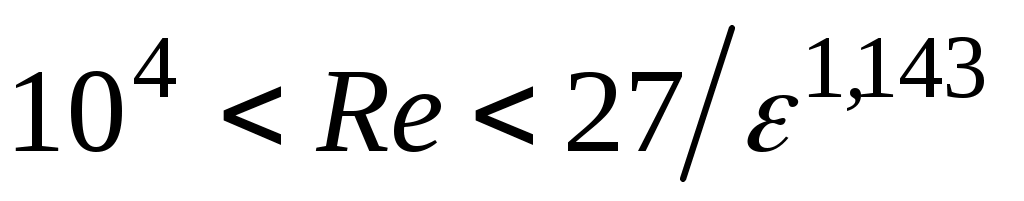 ( (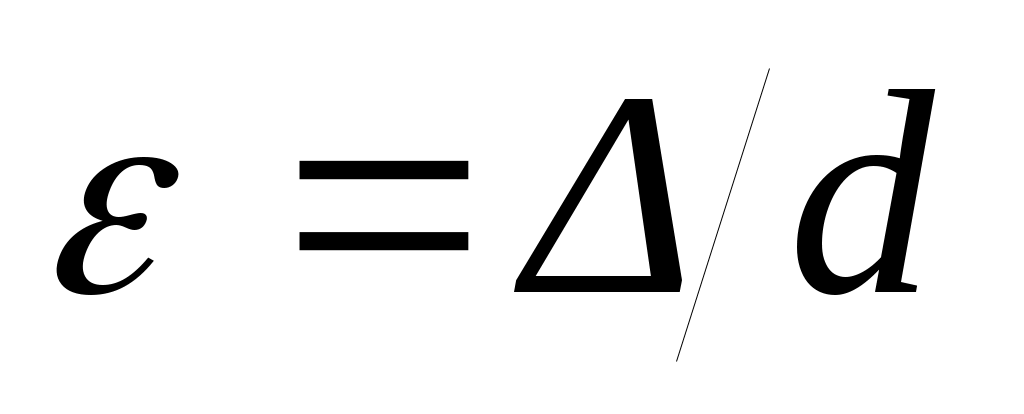 – относительная шероховатость внутренней поверхности трубопровода, являющаяся отношением абсолютной шероховатости Δ труб и внутреннего диаметра d трубопровода), то течение нефти происходит в развитом турбулентном режиме, в зоне так называемых «гидравлически гладких труб» (коэффициент – относительная шероховатость внутренней поверхности трубопровода, являющаяся отношением абсолютной шероховатости Δ труб и внутреннего диаметра d трубопровода), то течение нефти происходит в развитом турбулентном режиме, в зоне так называемых «гидравлически гладких труб» (коэффициент 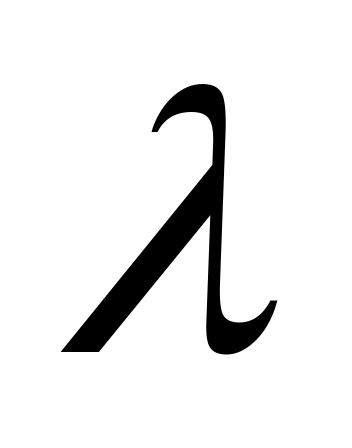 не зависит от шероховатости): не зависит от шероховатости):
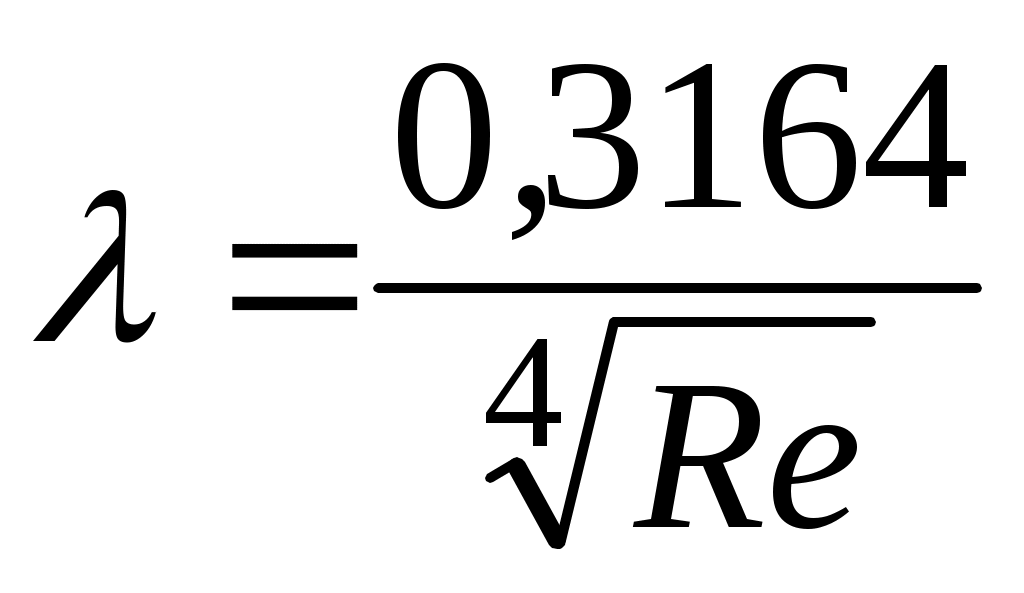 (формула Блазиуса). (1.9) (формула Блазиуса). (1.9)
Если 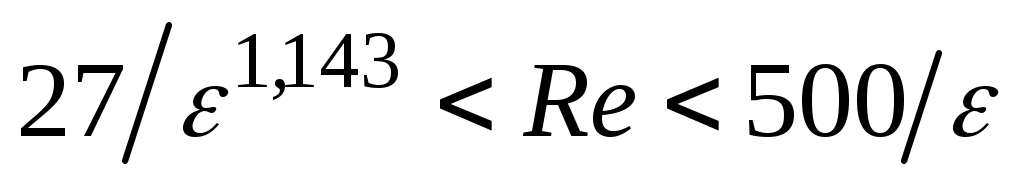 , то течение нефти происходит в зоне так называемого «смешанного трения», для которой коэффициент гидравлического сопротивления можно вычислить, например, по формуле: , то течение нефти происходит в зоне так называемого «смешанного трения», для которой коэффициент гидравлического сопротивления можно вычислить, например, по формуле:
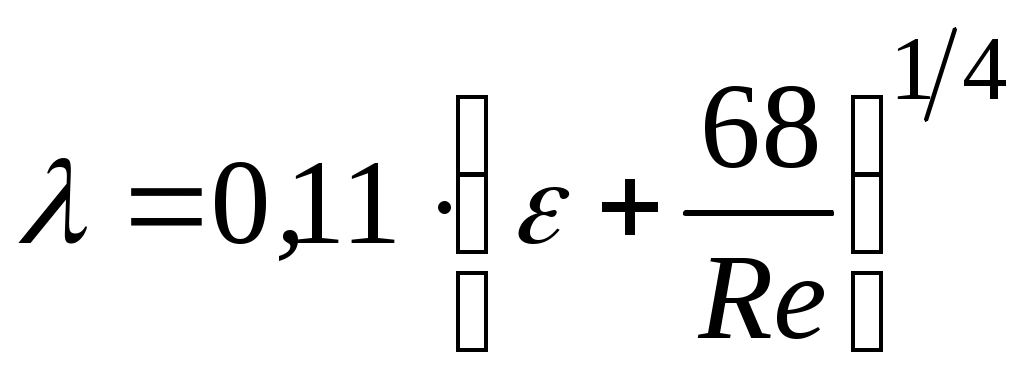 (формула Альтшуля). (1.10) (формула Альтшуля). (1.10)
Если 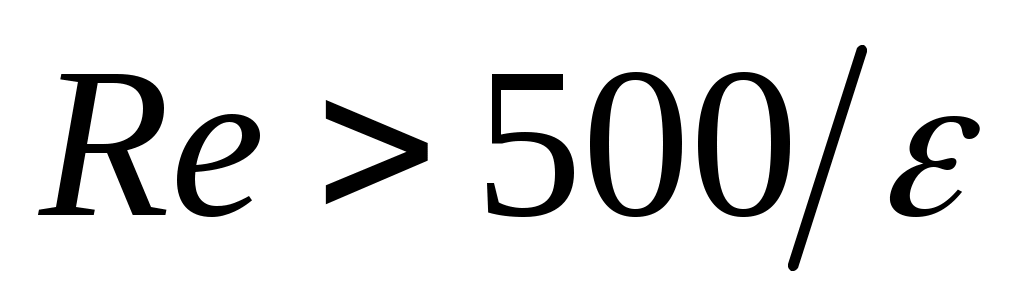 , то течение нефти происходит в зоне «квадратичного трения» (т. к. если , то течение нефти происходит в зоне «квадратичного трения» (т. к. если 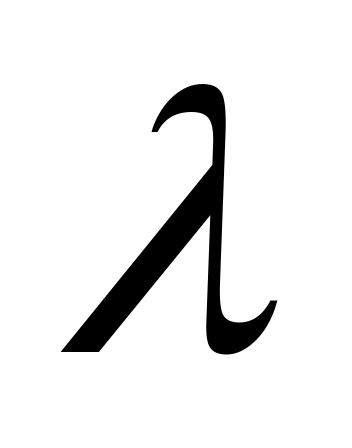 не зависит от скорости течения, то потери напора пропорциональны квадрату скорости течения) и не зависит от скорости течения, то потери напора пропорциональны квадрату скорости течения) и
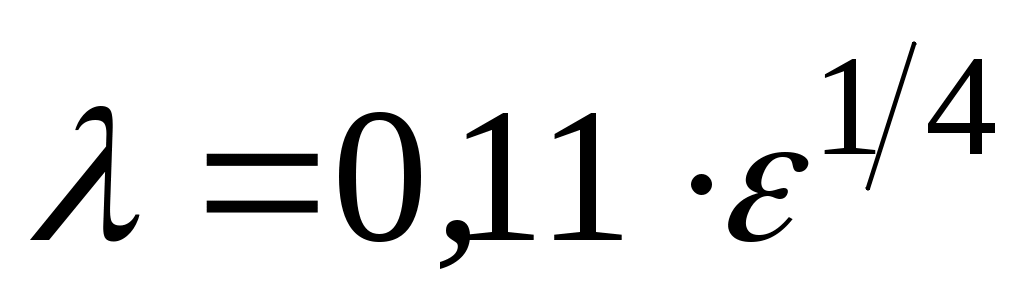 (формула Шифринсона). (1.11) (формула Шифринсона). (1.11)
Гидравлический уклон. Прямая АВ, представляющая зависимость полного напора  от координаты от координаты 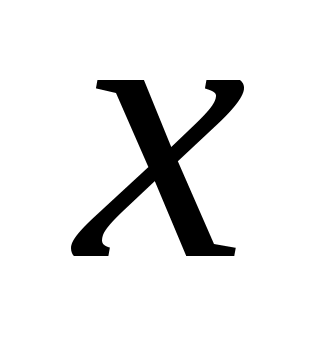 вдоль оси трубопровода: вдоль оси трубопровода: 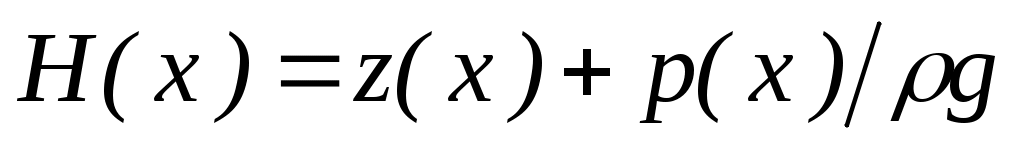 (рис.1) называется линией гидравлического уклона. Абсолютная величина тангенса угла (рис.1) называется линией гидравлического уклона. Абсолютная величина тангенса угла  ее наклона к горизонтали называется гидравлическим уклоном: ее наклона к горизонтали называется гидравлическим уклоном:
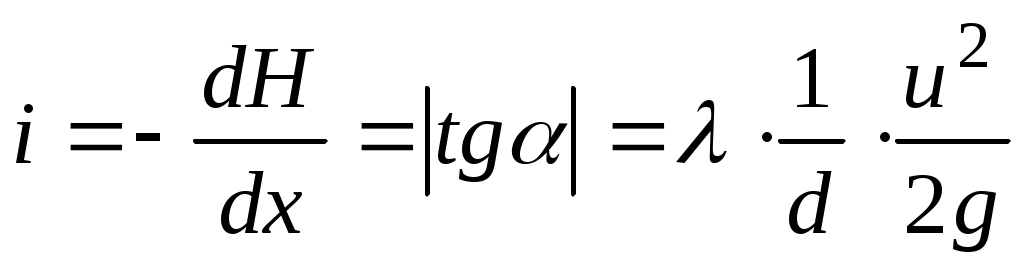 ; ; 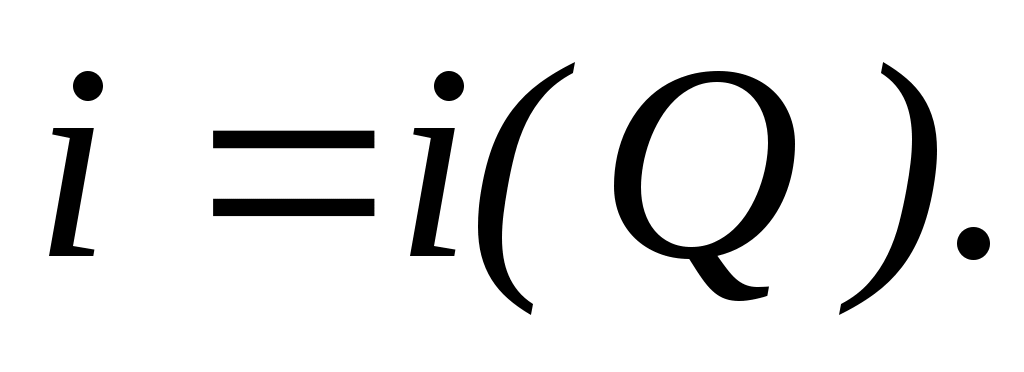 (1.12) (1.12)
Гидравлический уклон – это безразмерная величина, характеризующая быстроту падения напора в рассматриваемом нефтепроводе. Гидравлический уклон для данного нефтепровода зависит от производительности  перекачки, при этом, чем больше перекачки, при этом, чем больше  , тем быстрей уменьшается напор, тем больше величина гидравлического уклона , тем быстрей уменьшается напор, тем больше величина гидравлического уклона 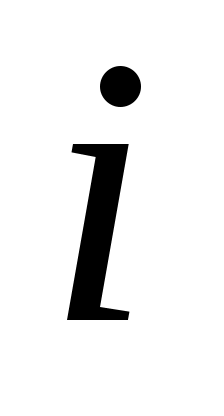 . .
Величина 1000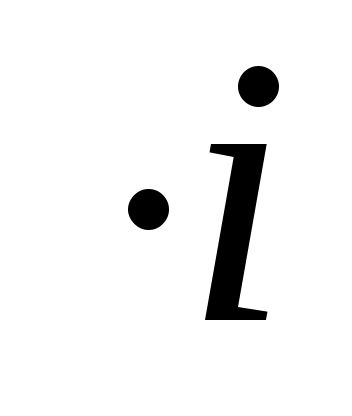 дает падение напора в м на км пути. Так, например, гидравлический уклон дает падение напора в м на км пути. Так, например, гидравлический уклон 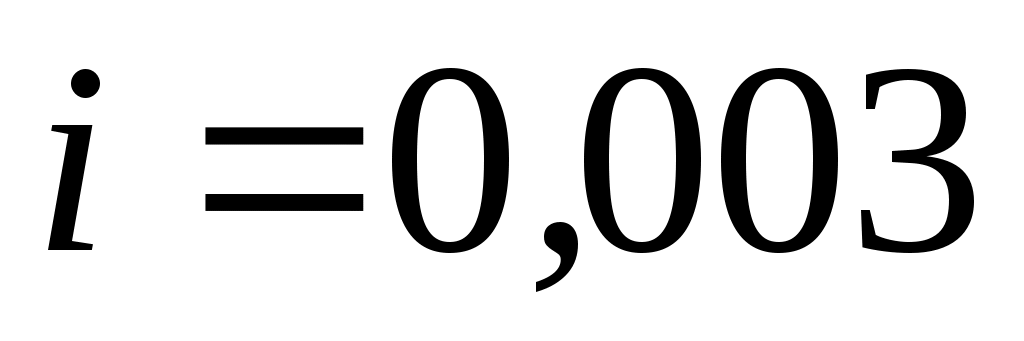 означает падение напора 3 м на 1 км пути, означает падение напора 3 м на 1 км пути, 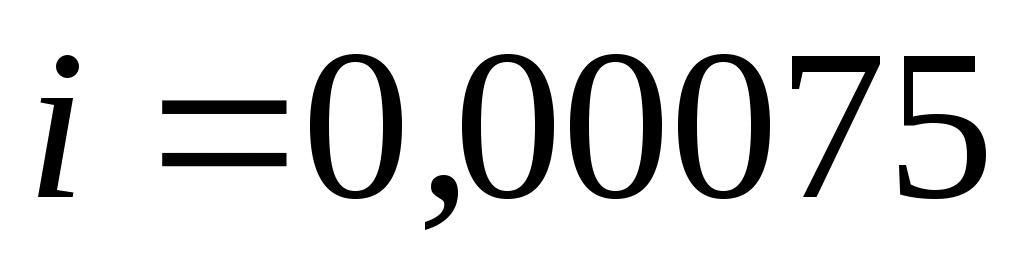 – 0,75 м на 1 км пути и т. д. – 0,75 м на 1 км пути и т. д.
Уравнение баланса напоров для участка нефтепровода. Начальный напор 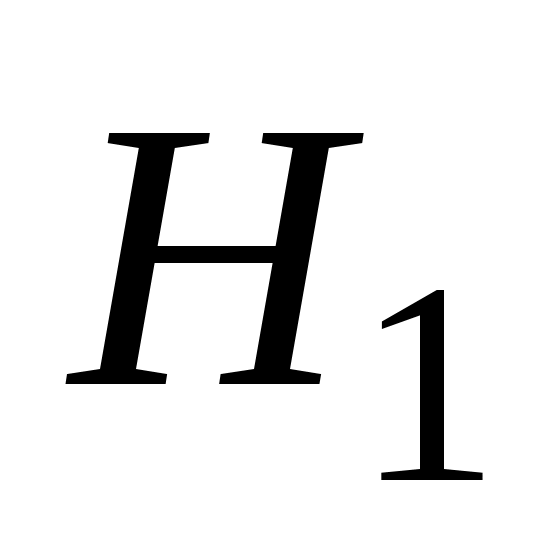 в линии нагнетания перекачивающей станции складывается из трех составляющих (см. рис.1): в линии нагнетания перекачивающей станции складывается из трех составляющих (см. рис.1):
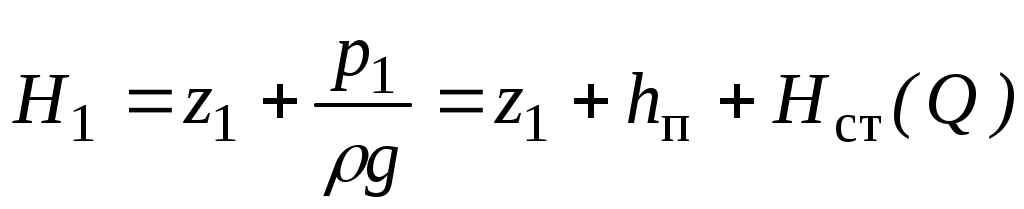 , ,
где 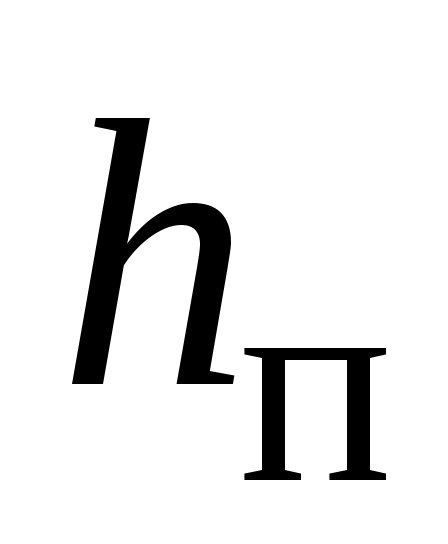 – подпор перед станцией (напор в линии всасывания станции) и – подпор перед станцией (напор в линии всасывания станции) и 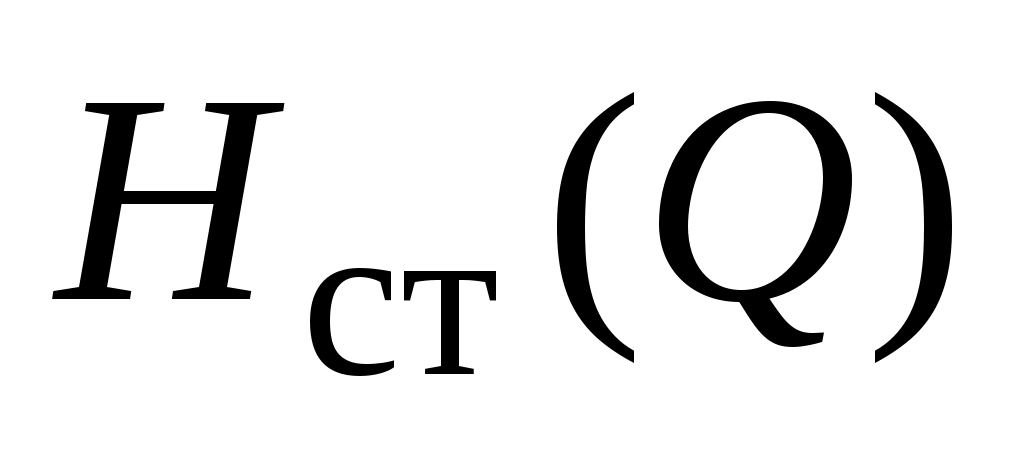 – дифференциальный напор станции (т.е. напор, создаваемый насосами станции). Последний зависит от производительности – дифференциальный напор станции (т.е. напор, создаваемый насосами станции). Последний зависит от производительности  нефтепровода и определяется, главным образом, нефтепровода и определяется, главным образом, 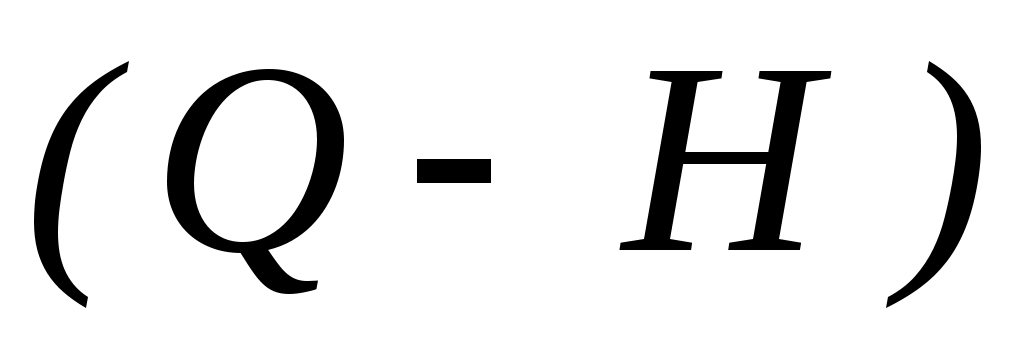 –характеристиками насосов, их типом и числом, а также характеристиками трубопроводной обвязки станции. –характеристиками насосов, их типом и числом, а также характеристиками трубопроводной обвязки станции.
Напор 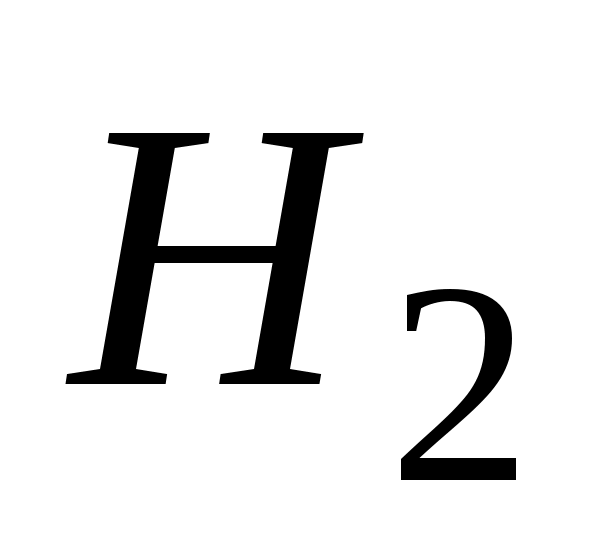 в конце участка нефтепровода складывается из двух составляющих: геометрического напора в конце участка нефтепровода складывается из двух составляющих: геометрического напора 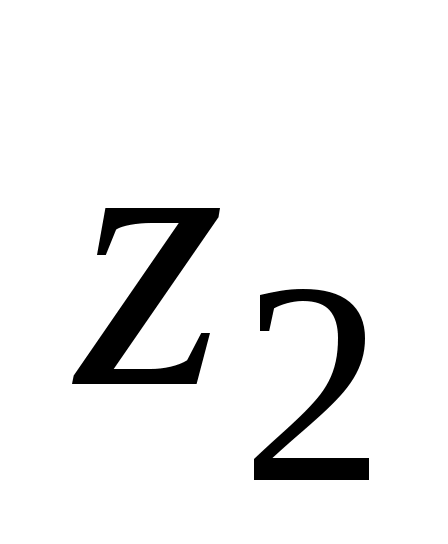 и конечного напора и конечного напора 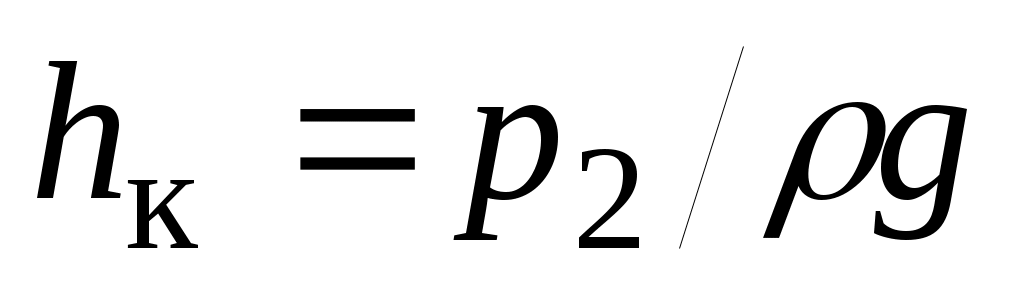 : :
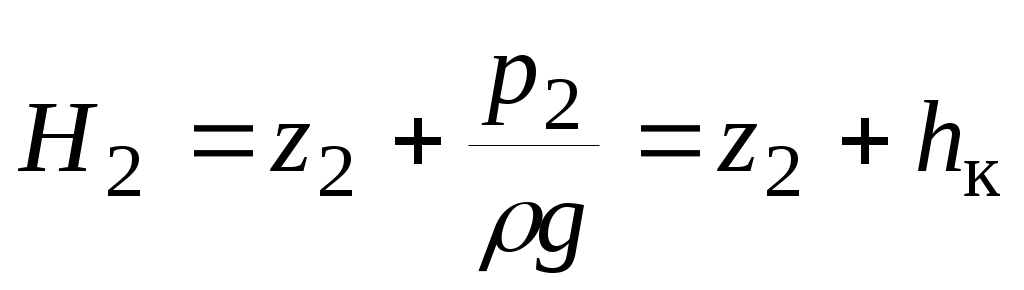 . .
Уравнение Бернулли (1.1), записанное для начального и конечного сечений участка нефтепровода, имеет вид:
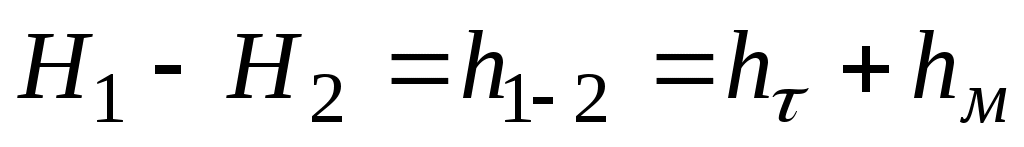 , ,
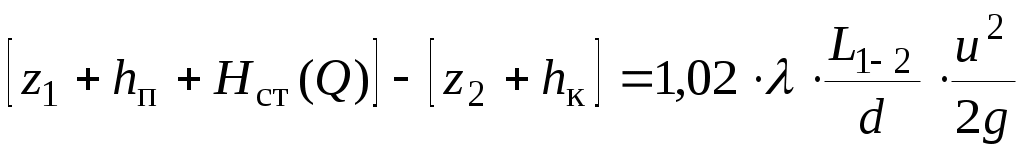
или
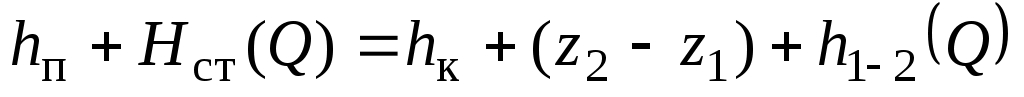 . (1.13) . (1.13)
Это уравнение называется уравнением баланса напоров для участка нефтепровода. Оно служит для определения производительности  перекачки. В левой части уравнения стоит пьезометрический напор перекачки. В левой части уравнения стоит пьезометрический напор 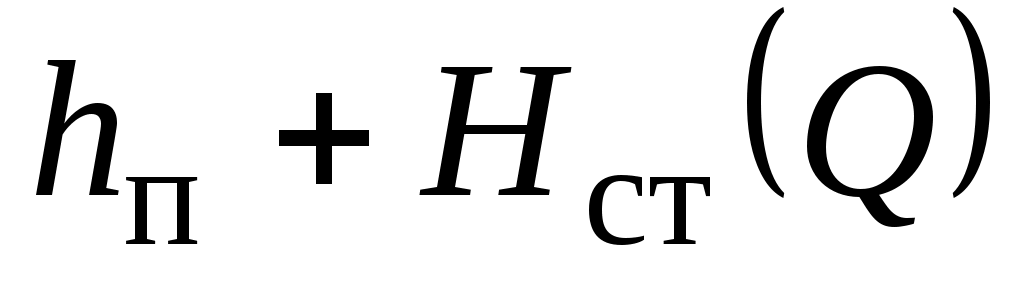 , имеющийся в начале нефтепровода, а в правой – сумма двух «противонапоров» , имеющийся в начале нефтепровода, а в правой – сумма двух «противонапоров» 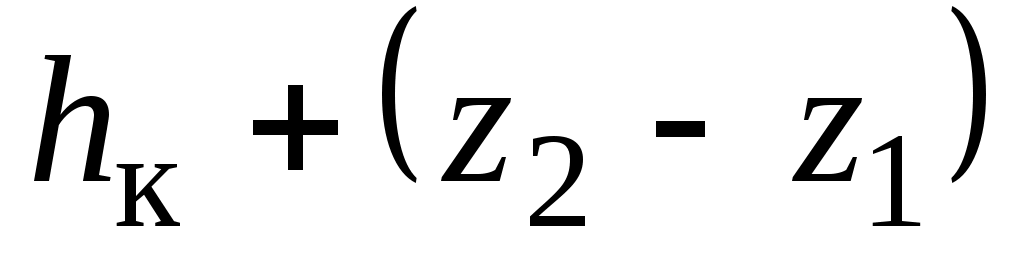 и потерь и потерь 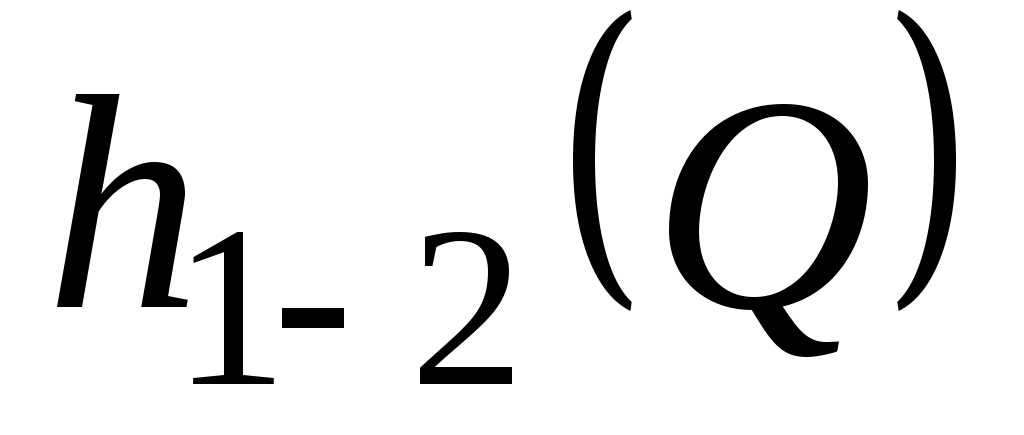 напора на рассматриваемом участке. Иными словами, уравнение (1.13) означает, что имеющийся в начале участка нефтепровода напор компенсирует противонапоры и потери напора из-за работы сил вязкого трения слоев нефти друг о друга. напора на рассматриваемом участке. Иными словами, уравнение (1.13) означает, что имеющийся в начале участка нефтепровода напор компенсирует противонапоры и потери напора из-за работы сил вязкого трения слоев нефти друг о друга.
На рис.2 представлена графическая интерпретация уравнения (1.13).
На плоскости переменных 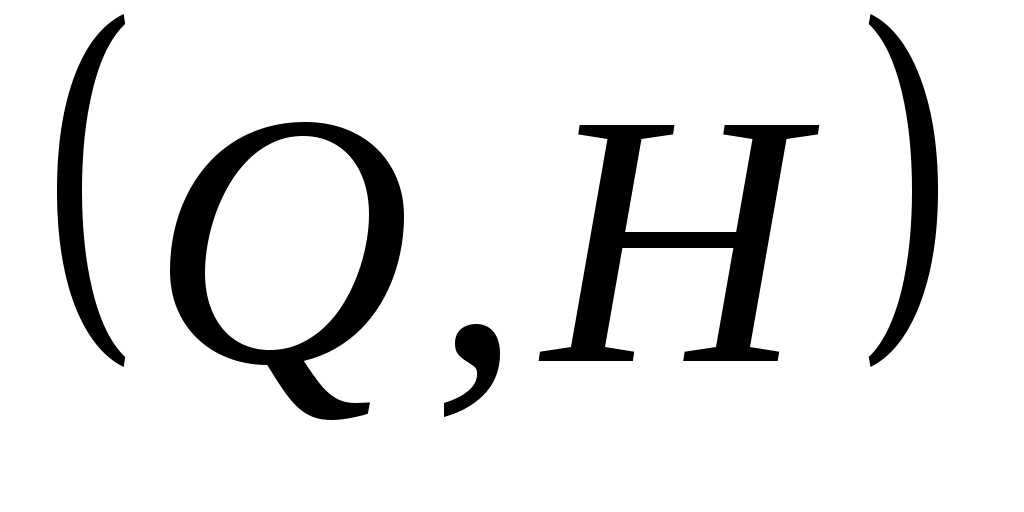 изображены графики левой и правой части уравнения (1.13), называемых соответственно: изображены графики левой и правой части уравнения (1.13), называемых соответственно:
кривая 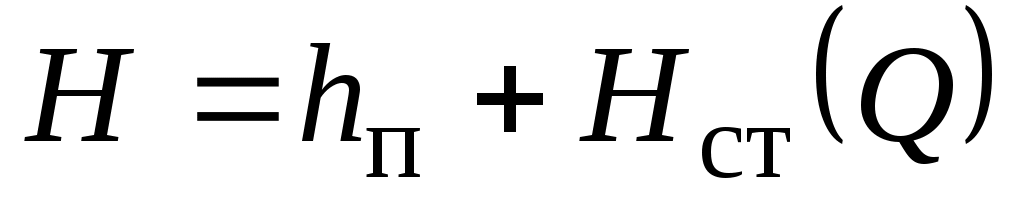 – (Q-H)–характеристикой нефтеперекачивающей станции; – (Q-H)–характеристикой нефтеперекачивающей станции;
кривая 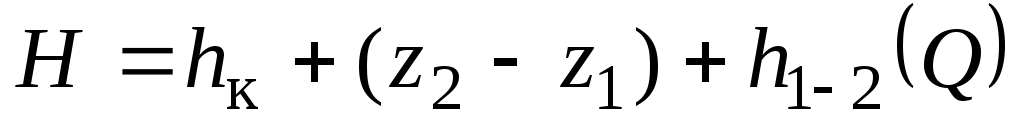 – (Q-H)–характеристикой участка нефтепровода. – (Q-H)–характеристикой участка нефтепровода.
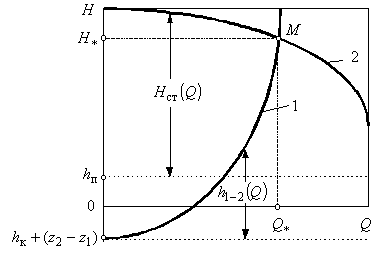
Рис.2. Совмещенные 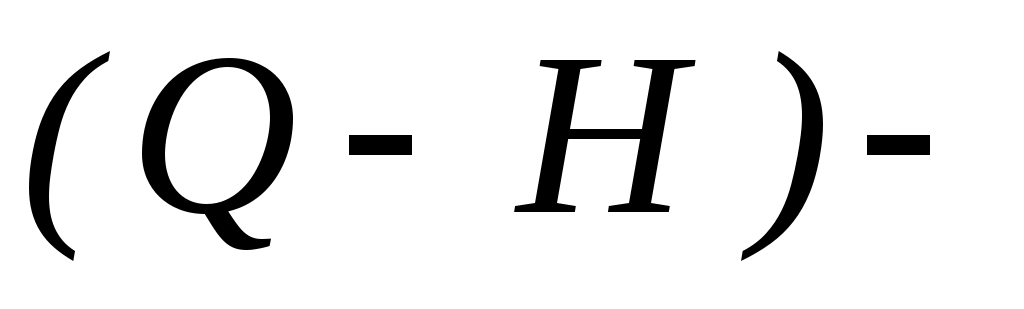 характеристики участка нефтепровода и нефтеперекачивающей станции (НПС): характеристики участка нефтепровода и нефтеперекачивающей станции (НПС):
1 – трубопровода, 2 - НПС
Координаты точки 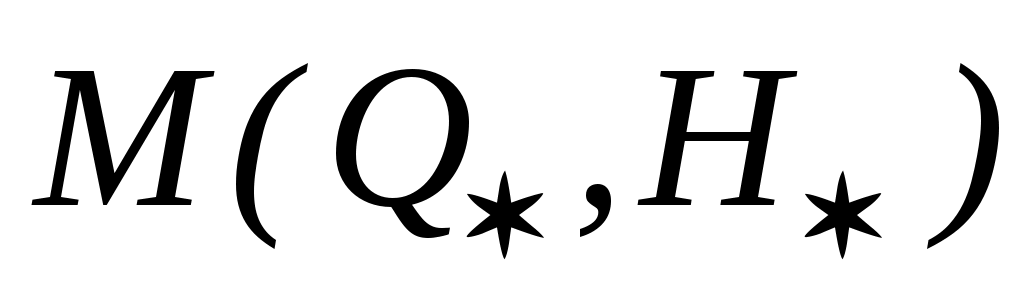 пересечения этих кривых, называемых также совмещенными (Q-H) – характеристиками нефтеперекачивающей станции и участка нефтепровода, дают графическое решение уравнения (1.13). Абсцисса пересечения этих кривых, называемых также совмещенными (Q-H) – характеристиками нефтеперекачивающей станции и участка нефтепровода, дают графическое решение уравнения (1.13). Абсцисса  точки точки 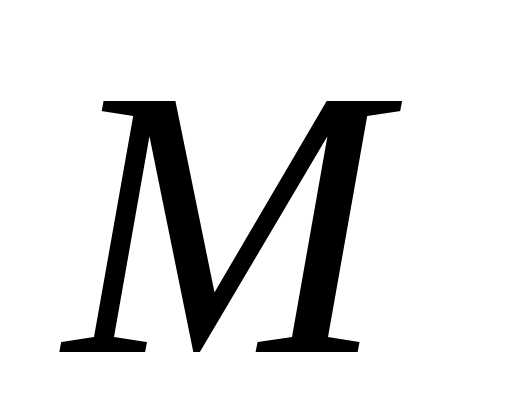 есть решение уравнения (1.13), а ее ордината есть решение уравнения (1.13), а ее ордината 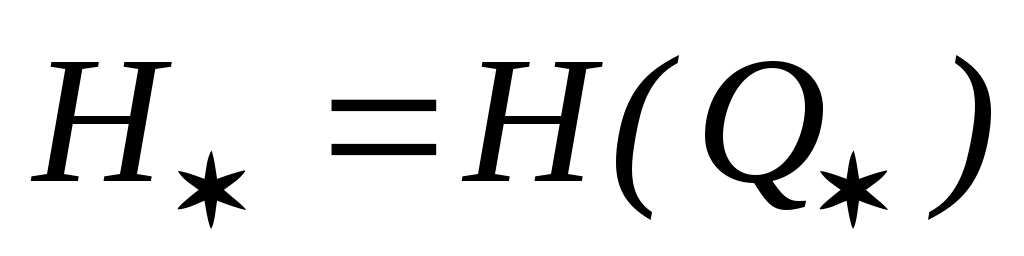 определяет напор на «выходе» станции. Точка определяет напор на «выходе» станции. Точка 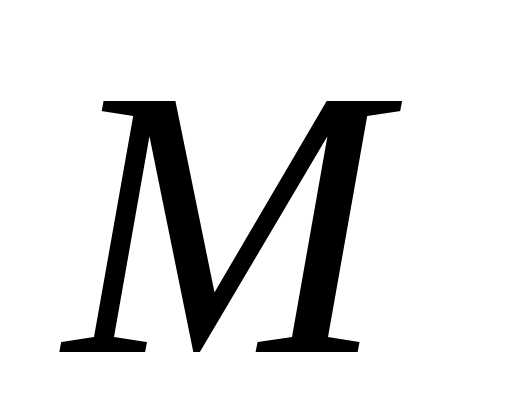 называется рабочей точкой системы «трубопровод - нефтеперекачивающая станция». называется рабочей точкой системы «трубопровод - нефтеперекачивающая станция».
Потери напора 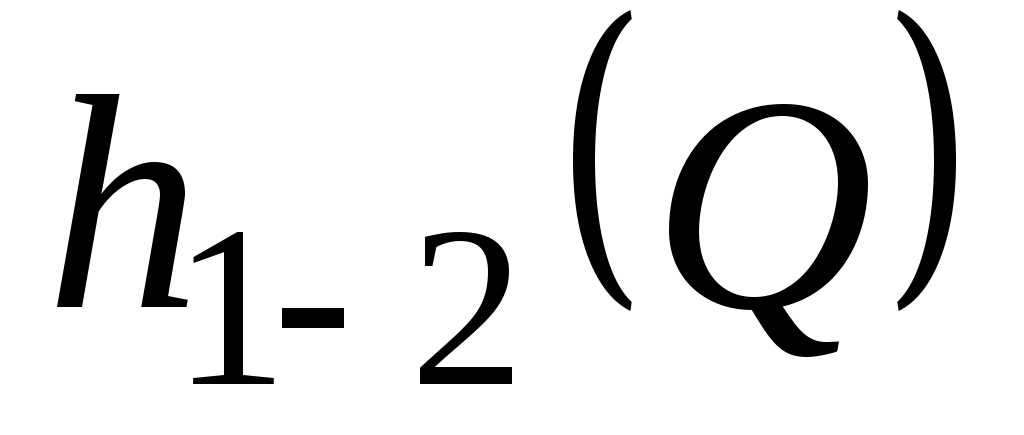 , входящие в (Q-H) – характеристику участка нефтепровода и происходящие из-за диссипации механической энергии вследствие сил вязкого трения слоев нефти друг о друга, представляются формулой (1.5) Дарси-Вейсбаха , входящие в (Q-H) – характеристику участка нефтепровода и происходящие из-за диссипации механической энергии вследствие сил вязкого трения слоев нефти друг о друга, представляются формулой (1.5) Дарси-Вейсбаха
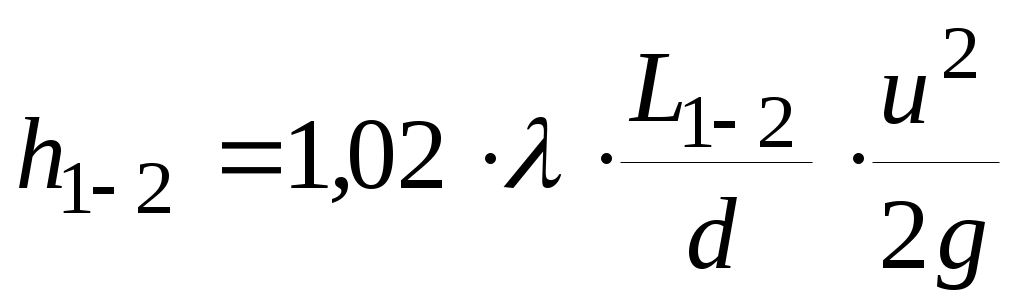
(с поправкой на местные сопротивления), в которой 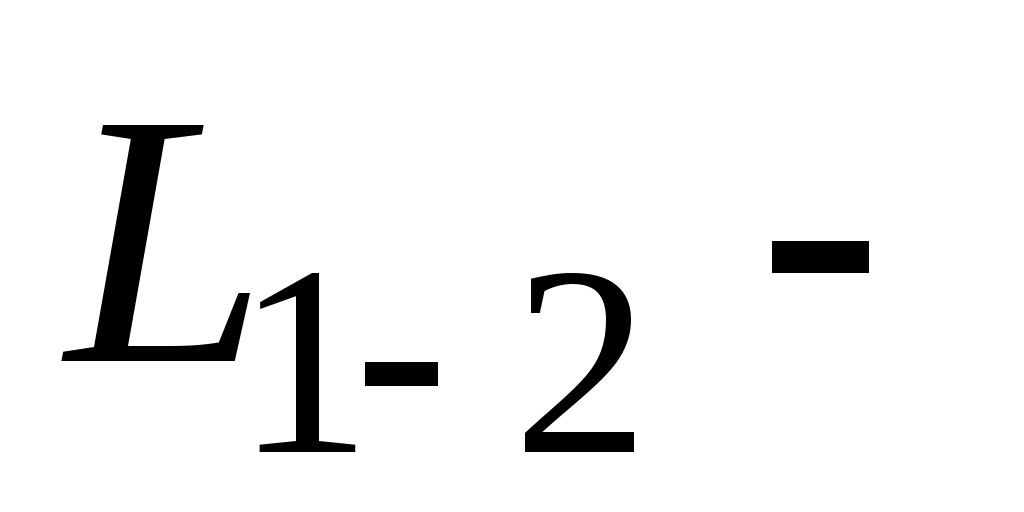 протяженность рассматриваемого участка нефтепровода. При этом предполагается, что участок полностью заполнен жидкостью. протяженность рассматриваемого участка нефтепровода. При этом предполагается, что участок полностью заполнен жидкостью.
Однако могут существовать режимы перекачки, в которых нефть на отдельных участках трубопровода движется неполным сечением или, как говорят, самотеком. Такие участки называются самотечными.
Самотечные участки нефтепровода. Самотечным называется участок [x1, x2] трубопровода, на котором нефть движется неполным сечением (самотеком) под действием силы тяжести (рис.3). [1, 4]
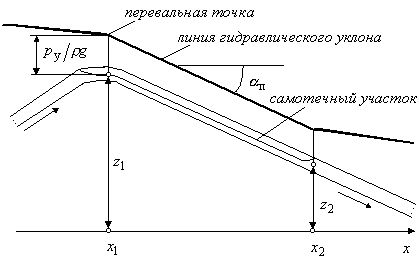
Рис.3. Схема самотечного участка нефтепровода
Давление в парогазовой полости остается практически постоянным и равным давлению pу упругости насыщенных паров данной нефти, поэтому течение на самотечном участке называется безнапорным. Однако разность напоров между сечениями 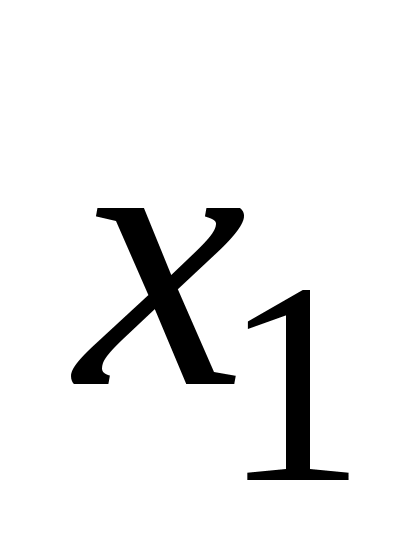 (началом самотечного участка) и (началом самотечного участка) и 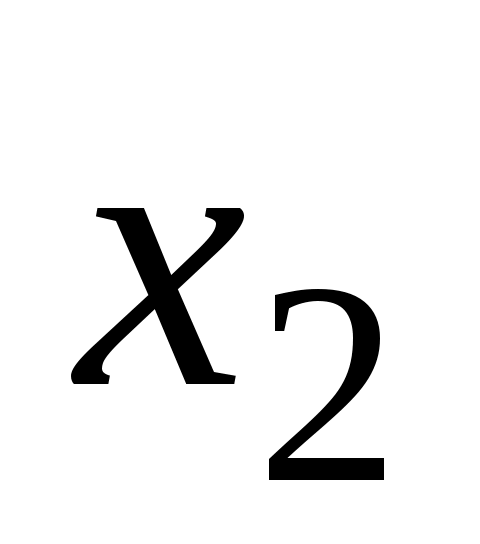 (концом самотечного участка) все же существует, она равна разности (концом самотечного участка) все же существует, она равна разности 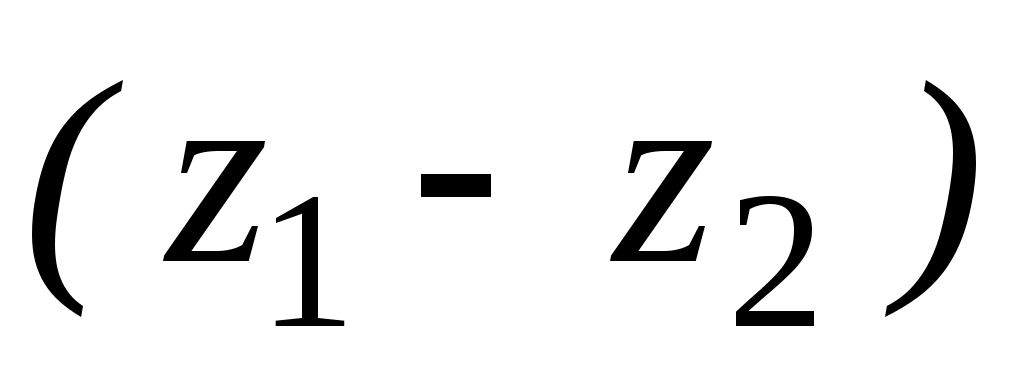 геометрических высот этих сечений. геометрических высот этих сечений.
Стационарные самотечные участки с расслоенным течением жидкости могут существовать только на нисходящих участках нефтепровода.
Начало 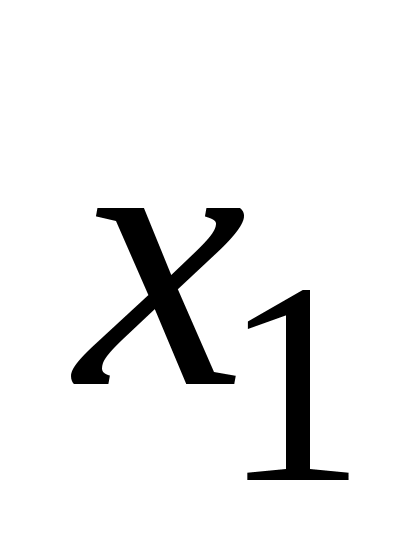 каждого самотечного участка называется перевальной точкой. Перевальная точка всегда совпадает с одной из вершин профиля трубопровода. каждого самотечного участка называется перевальной точкой. Перевальная точка всегда совпадает с одной из вершин профиля трубопровода.
Линия гидравлического уклона на самотечном участке проходит параллельно профилю трубопровода на расстоянии 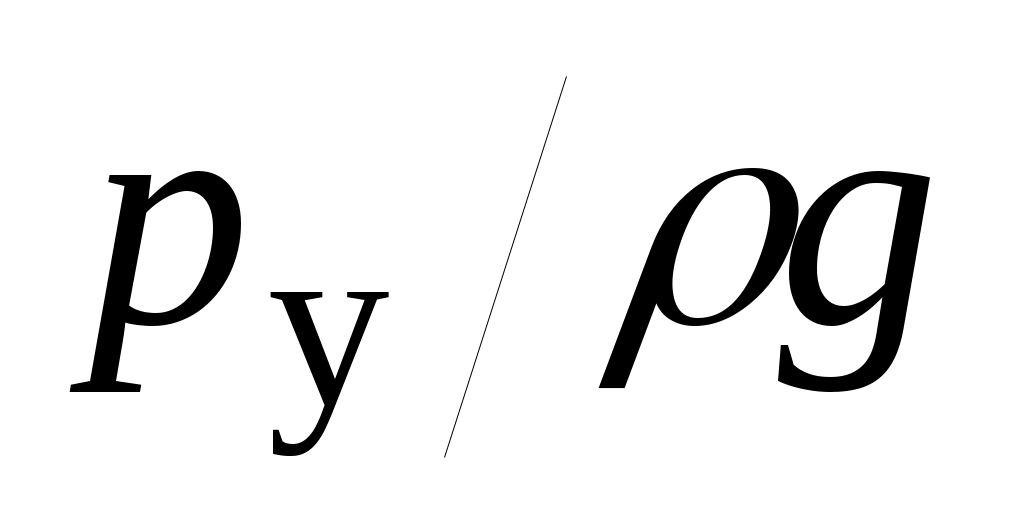 над ним. Отсюда следует, что гидравлический уклон iс на самотечном участке равен абсолютной величине тангенса угла αп наклона профиля нефтепровода к горизонту: над ним. Отсюда следует, что гидравлический уклон iс на самотечном участке равен абсолютной величине тангенса угла αп наклона профиля нефтепровода к горизонту: 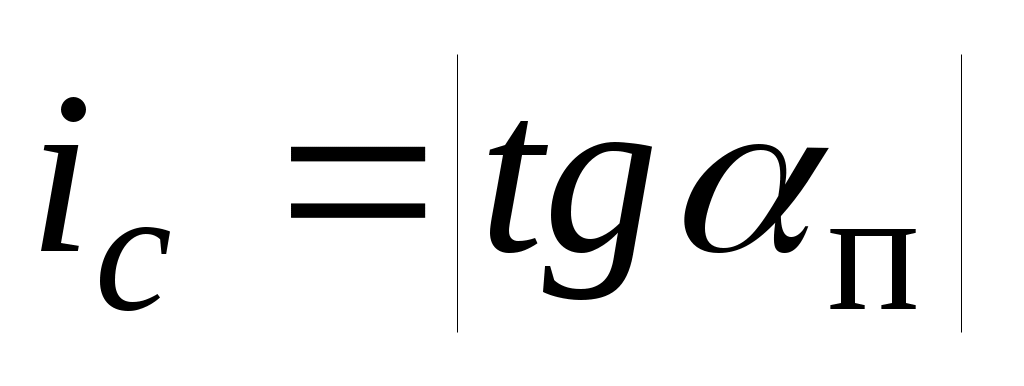 . .
Расход нефти на самотечном участке в стационарном режиме равен расходу  нефти в заполненных сечениях трубопровода: нефти в заполненных сечениях трубопровода:
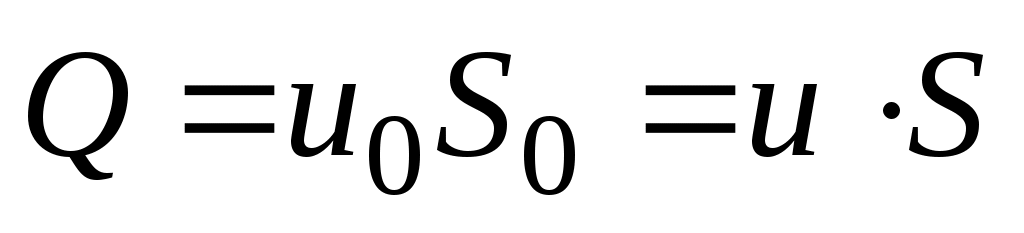 . (1.14) . (1.14)
Из чего можно заключить, что скорость  движения жидкости на самотечном участке больше скорости движения жидкости на самотечном участке больше скорости 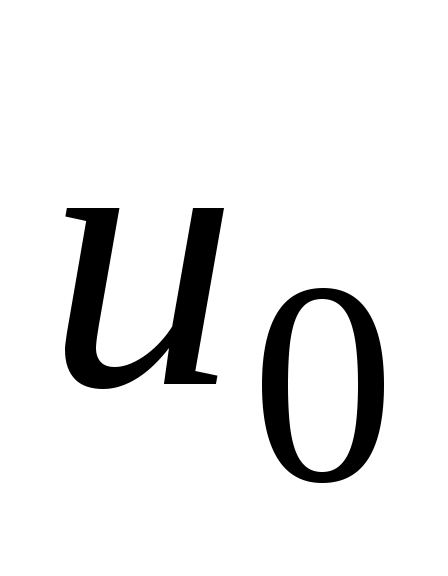 движения жидкости на заполненных участках нефтепровода, поскольку площадь движения жидкости на заполненных участках нефтепровода, поскольку площадь 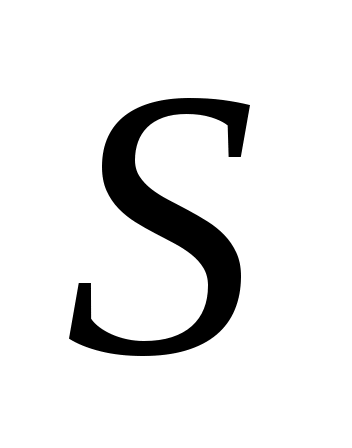 части сечения, занятого жидкостью на каждом самотечном участке, меньше площади части сечения, занятого жидкостью на каждом самотечном участке, меньше площади 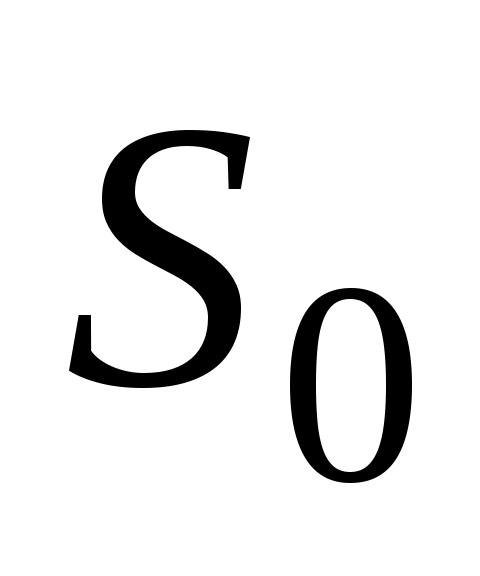 полного сечения трубопровода: полного сечения трубопровода: 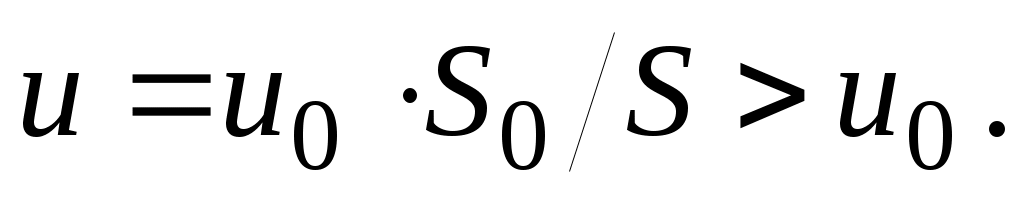
Степень 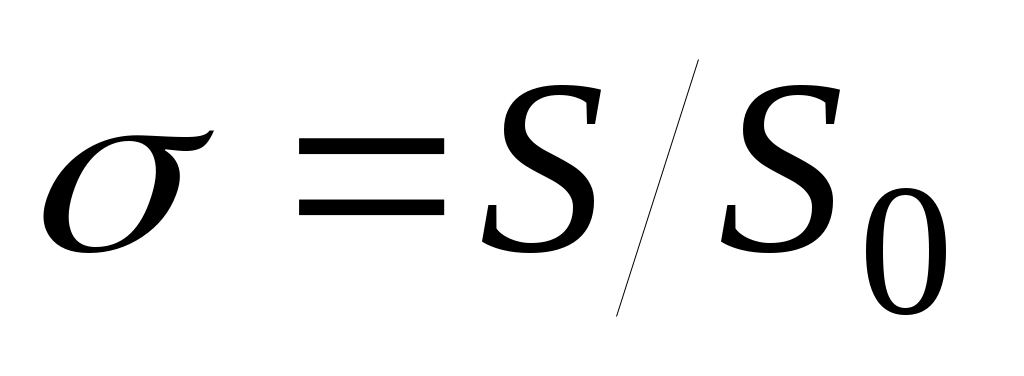 заполнения самотечного участка нефтью может быть различной. Она зависит от отношения заполнения самотечного участка нефтью может быть различной. Она зависит от отношения 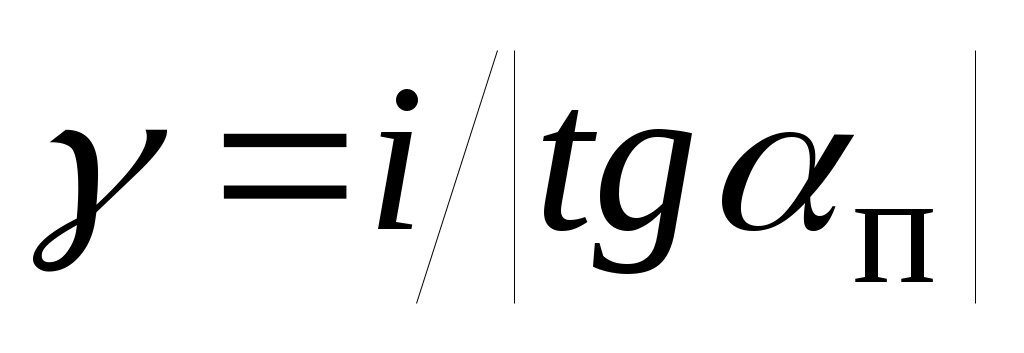 гидравлических уклонов на самотечном участке ( гидравлических уклонов на самотечном участке (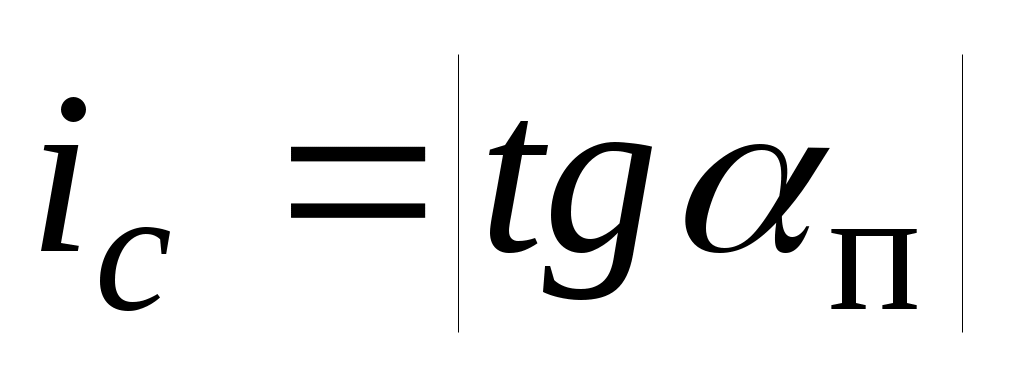 ) и на участках трубопровода, полностью заполненных нефтью ( ) и на участках трубопровода, полностью заполненных нефтью (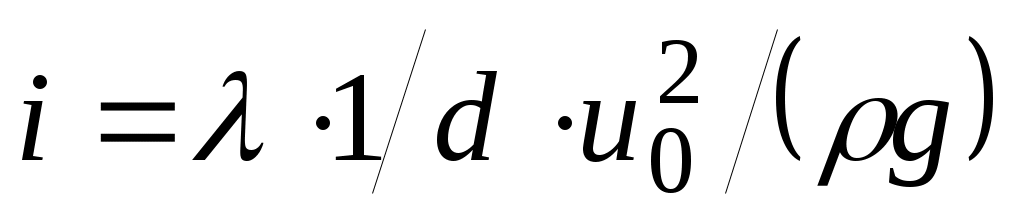 ). Обобщая многочисленные исследования в области безнапорных течений в каналах кругового сечения, можно предложить следующие аппроксимационные формулы для расчета степени заполнения сечения трубы нефтью на самотечном участке при расслоенном течении. ). Обобщая многочисленные исследования в области безнапорных течений в каналах кругового сечения, можно предложить следующие аппроксимационные формулы для расчета степени заполнения сечения трубы нефтью на самотечном участке при расслоенном течении.
Если 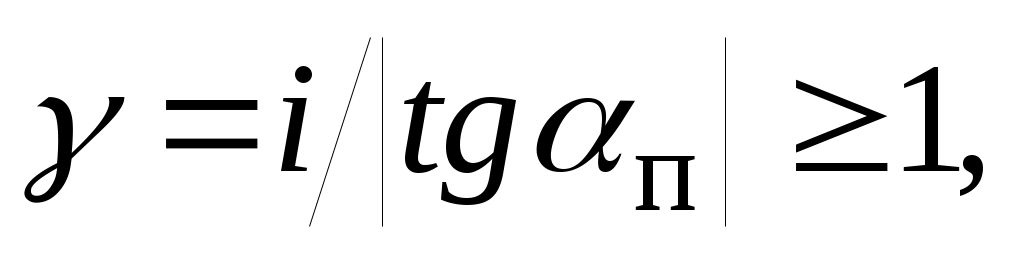 то то 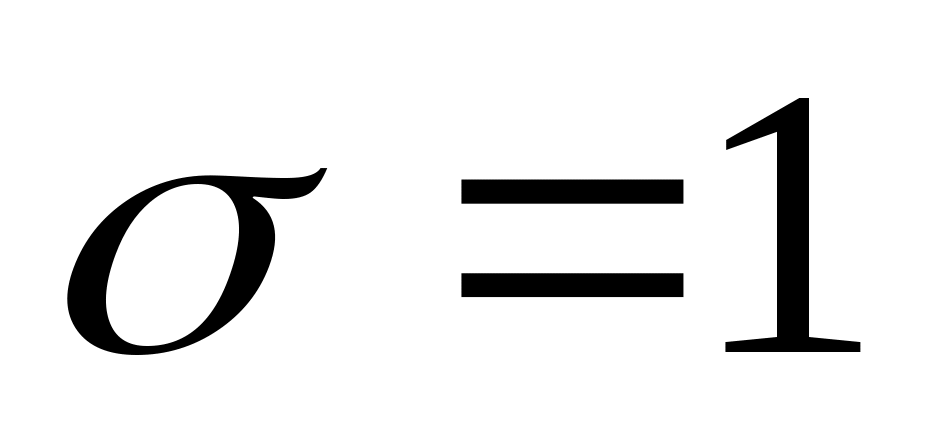 . В этом случае сечение трубы заполнено полностью. . В этом случае сечение трубы заполнено полностью.
Если 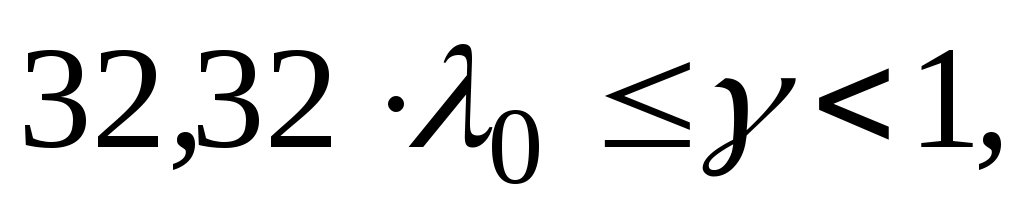 то то
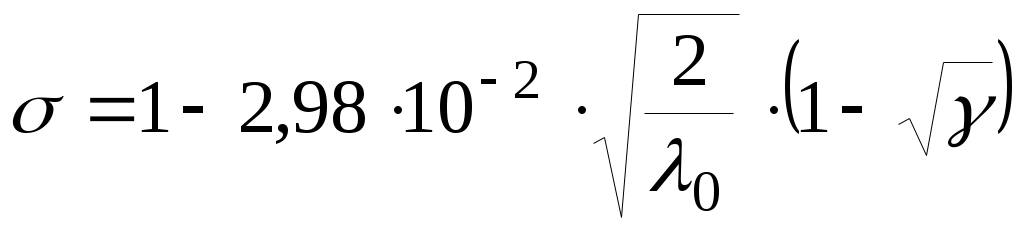 . .
Если 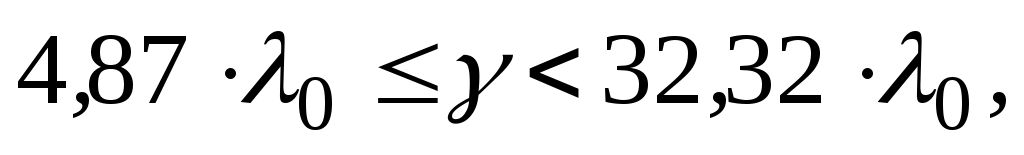 то то
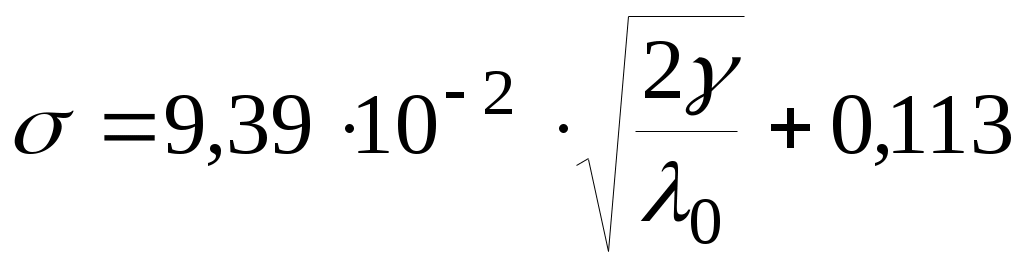 . (1.15) . (1.15)
Если 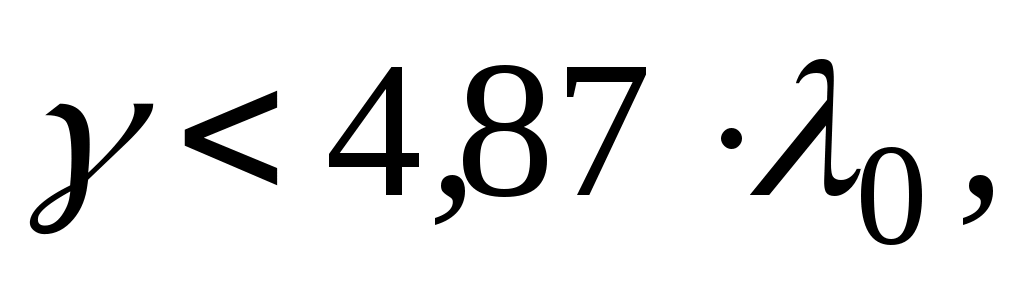 то то
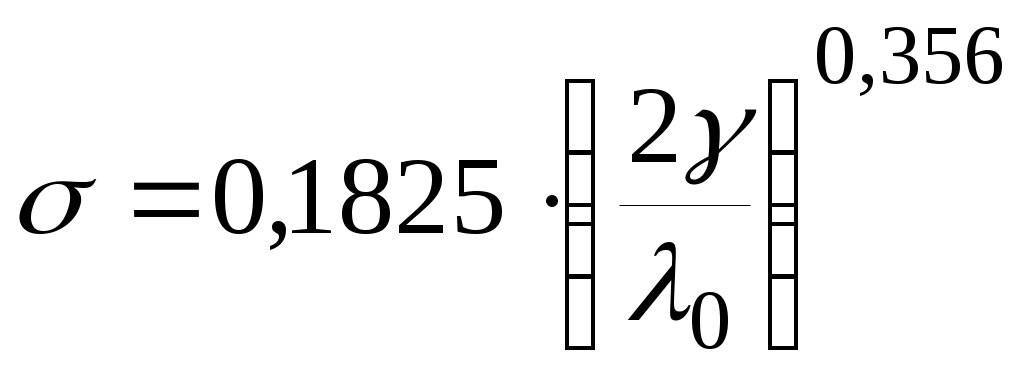 . .
Формулы (1.15) позволяют рассчитать степень заполнения 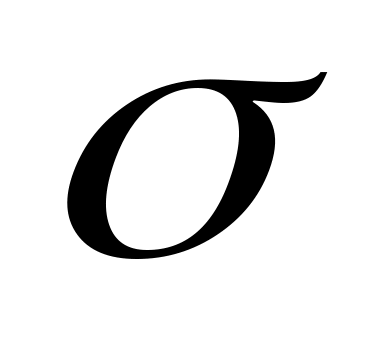 сечения трубопровода нефтью по известному отношению сечения трубопровода нефтью по известному отношению 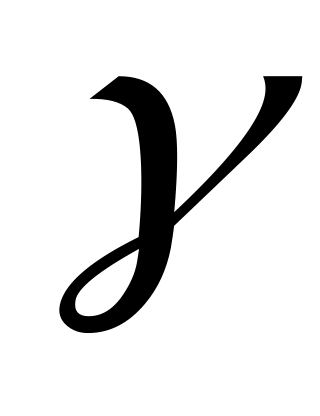 гидравлических уклонов гидравлических уклонов 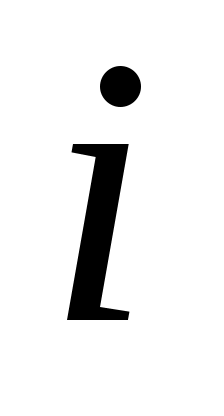 и и 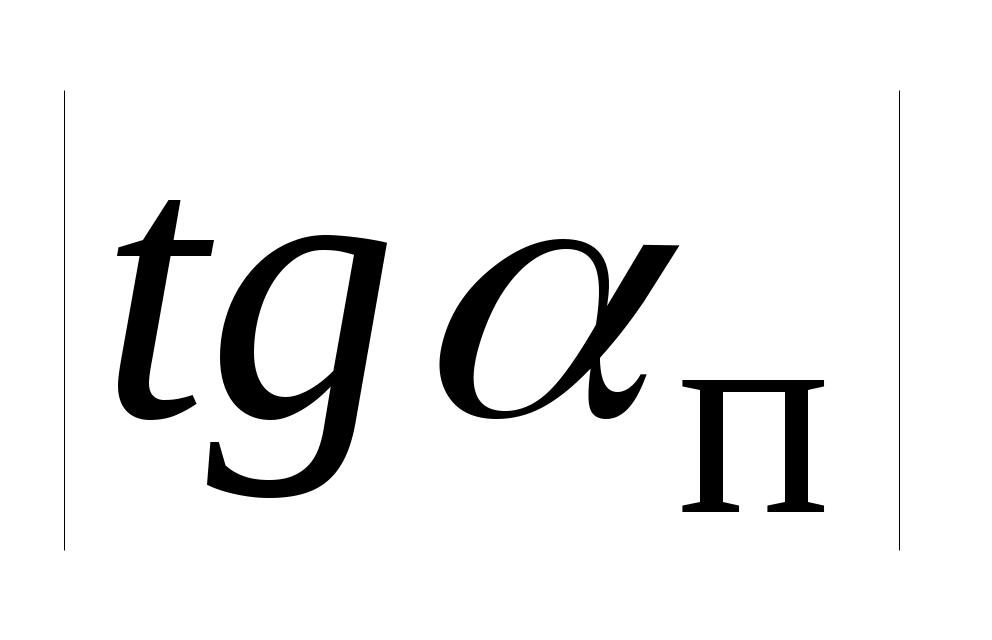 на напорном и самотечном участках, соответственно. на напорном и самотечном участках, соответственно.
|
 Скачать 2.33 Mb.
Скачать 2.33 Mb.