Лабораторная работа 3. Лабораторная работа 1 Разработка и анализ простых криптографических алгоритмов на основе методов перестановок и подстановок

• Название: Лабораторная работа 1 Разработка и анализ простых криптографических алгоритмов на основе методов перестановок и подстановок
• Дата: 31.01.2022
• Размер: 412 Kb.
• Имя файла: Лабораторная работа 3.doc
• Тип: Лабораторная работа; #346875

Лабораторная работа № 1

Разработка и анализ простых криптографических алгоритмов на основе методов перестановок и подстановок

Цель работы: получение навыков создания простейшей криптосистемы симметричного шифрования.

Краткие теоретические сведения

Основные понятия криптографии

Криптография представляет собой совокупность методов преобразования данных, направленных на то, чтобы сделать эти данные бесполезными для противника. Такие преобразования позволяют решить две главные проблемы защиты данных: проблему конфиденциальности (путем лишения противника возможности извлечь информацию из канала связи) и проблему целостности (путем лишения противника возможности изменить сообщение так, чтобы изменился его смысл, или ввести ложную информацию в канал связи).

Система защиты информации, основанная на методах криптографии обычно называется криптографической системой, или более коротко – криптосистемой. Обобщенная схема криптографической системы показана на рис. 1.1.



Рис. 1.1. Обобщенная схема криптосистемы

Согласно этой схемы, отправитель генерирует открытый текст исходного сообщения М, которое должно быть передано законному получателю по незащищенному каналу. За каналом следит перехватчик с целью перехватить и раскрыть передаваемое сообщение. Для того чтобы перехватчик не смог узнать содержание сообщения М, отправитель шифрует его с помощью обратимого преобразования E_Kи получает шифртекст (или криптограмму) C=E_K(M), который отправляет получателю.

Законный получатель, приняв криптограмму C, расшифровывает его с помощью обратного преобразования D_K=E_K^-1 и получает исходное сообщение в виде открытого текста М:

D_K (C) = E_K^-1(E_K(M) = M.

Преобразование E_K выбирается из семейства криптографических преобразований, называемых криптоалгоритмами. Параметр, с помощью которого выбирается отдельное используемое преобразование, называется криптографическим ключом K.

Таким образом, процесс преобразования открытого текста с целью сделать непонятным его смысл для посторонних называется шифрованием. В результате шифрования получается шифртекст. Процесс обратного преобразования шифртекста в открытый текст называется расшифрованием.

Под шифром понимают совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, задаваемых ключом и алгоритмом криптографического преобразования.

Криптосистема имеет разные варианты реализации: набор инструкций, аппаратные средства, комплекс программ компьютера, которые позволяют зашифровать открытый текст и расшифровать шифортекст различными способами, один из которых выбирается с помощью конкретного ключа K.

Говоря более формально, криптографическая система – это однопараметрическое семейство обратимых преобразований:





из пространства сообщений открытого текста в пространство шифрованных текстов и наоборот, причем D_K=E_K^-1. Параметр K (ключ) выбирается из конечного множества , называемого пространством ключей.

Криптосистемы, в которых применятся один и тот же секретный ключ, как при шифровании, так и при расшифровании сообщений, называются симметричными.

Проблема криптографического преобразования информации интересует человечество на протяжении нескольких тысячелетий. Шифры, дошедшие до нас с древнейших времен, основаны на двух основных принципах: перестановке и замене (подстановки).

Шифры перестановки

Шифрование перестановкой заключается в том, что символы открытого текста переставляются по определенному правилу в пределах некоторого блока этого текста. Рассмотрим перестановку, предназначенную для шифрования сообщения длиной nсимволов. Его можно представить спомощью таблицы

,

где i₁ – номер места шифртекста, на которое попадает первая буква открытого текста при выбранном преобразовании, i₂— номер места для второй буквы и т. д. В верхней строке таблицы выписаны по порядку числа от 1 до n, а в нижней те же числа, но в произвольном порядке. Такая таблица называется перестановкой степени n.

Зная перестановку, задающую преобразование, можно осуществить как шифрование, так и расшифрование текста. В этом случае, сама таблица перестановки служит ключом шифрования.

Число различных преобразований шифра перестановки, предназначенного для шифрования сообщений длины n, меньше либо равно n! (n факториал).Заметим, что в это число входит и вариант преобразования, оставляющий все символы на своих местах.

С увеличением числа nзначение n!растет очень быстро. Для использования на практике такой шифр не удобен, так как при больших значениях nприходится работать с длинными таблицами. Поэтому широкое распространение получили шифры, использующие не саму таблицу перестановки, а некоторое правило, порождающее эту таблицу. Рассмотрим несколько примеров таких шифров.

Шифр перестановки "скитала". Известно, что в V веке до нашей эры правители Спарты, наиболее воинственного из греческих государств, имели хорошо отработанную систему секретной военной связи и шифровали свои послания с помощью скитала, первого простейшего криптографического устройства, реализующего метод простой перестановки.

Шифрование выполнялось следующим образом. На стержень цилиндрической формы, который назывался скитала, наматывали спиралью (виток к витку) полоску пергамента и писали на ней вдоль стержня несколько строк текста сообщения (рис. 1.2). Затем снимали со стержня полоску пергамента с написанным текстом. Буквы на этой полоске оказывались расположенными хаотично.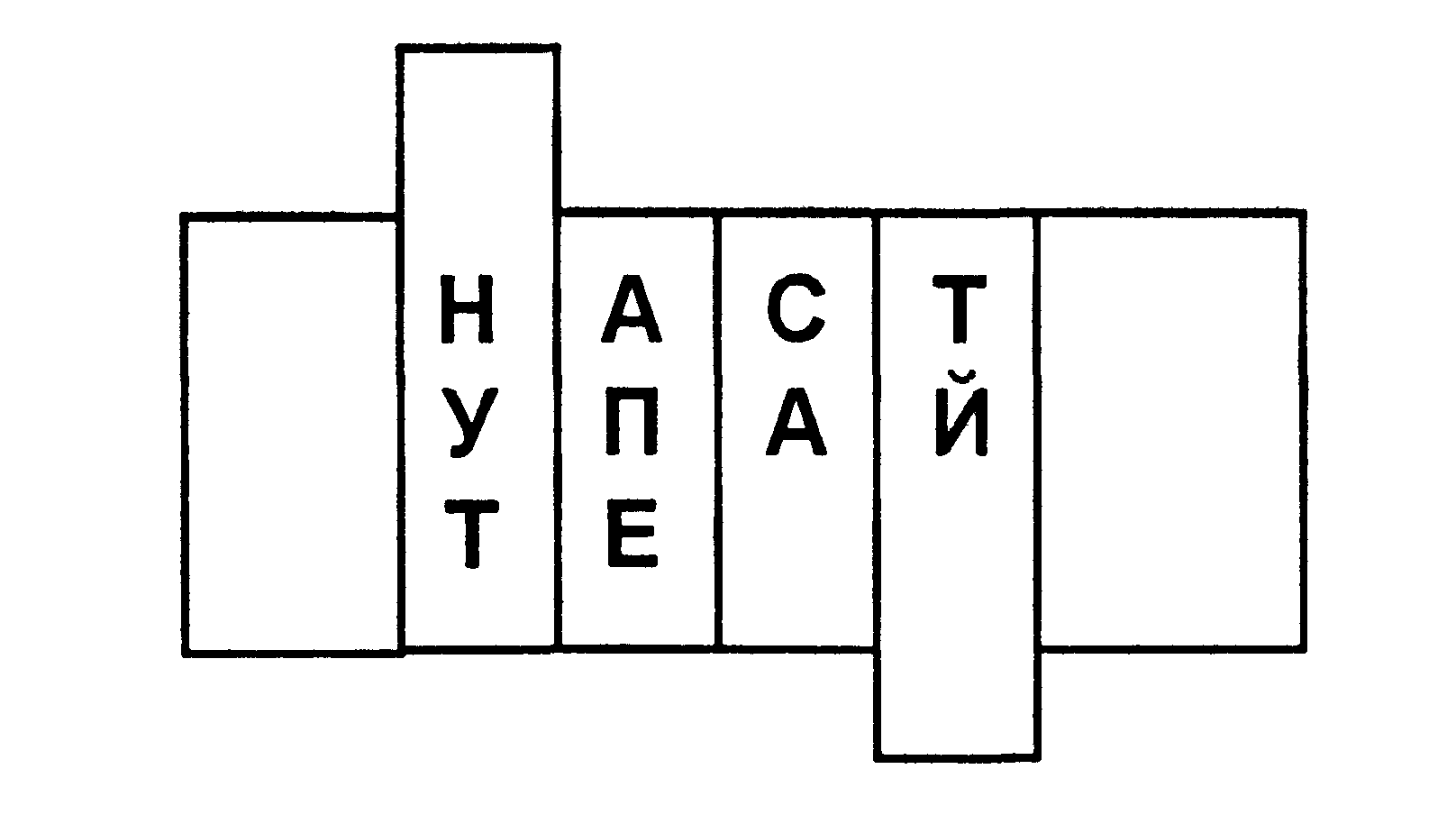



Рис. 1.2. Шифр "Скитала"

Такой же результат можно получить, если буквы сообщения писать по кольцу не подряд, а через определенное число позиций до тех пор, пока не будет исчерпан весь текст. Сообщение "НАСТУПАЙТЕ" при размещении его по окружности стержня по три буквы дает шифртекст: "НУТАПЕСА_ТЙ".

Для расшифрования такого шифртекста нужно не только знать правило шифрования, но и обладать ключом в виде стержня определенного диаметра. Зная только вид шифра, но не имея ключа, расшифровать сообщение было непросто.

Шифрующие таблицы. С начала эпохи Возрождения (конец XIV столетия) начала возрождаться и криптография. В разработанных шифрах перестановки того времени применяются шифрующие таблицы, которые, в сущности, задают правила перестановки букв в сообщении.

В качестве ключа в шифрующих таблицах используются:

1. 
   размер таблицы;
   
2. 
   слово или фраза, задающие перестановку;
   
3. 
   особенности структуры таблицы.
   

Одним из самых примитивных табличных шифров перестановки является простая перестановка, для которой ключом служит размер таблицы. Этот метод шифрования сходен с шифром скитала. Например, сообщение "ТЕРМИНАТОР ПРИБЫВАЕТ СЕДЬМОГО В ПОЛНОЧЬ" записывается в таблицу поочередно по столбцам. Результат заполнения таблицы из 5 строк и 7 столбцов показан на рис. 1.3.

После заполнения таблицы текстом сообщения по столбцам для формирования шифртекста считывают содержимое таблицы по строкам. Если шифртекст записывать группами по пять букв, получается такое шифрованное сообщение: "ТНПВЕ ГЛЕАР АДОНР ТИЕЬВ ОМОБТ МПЧИР ЫСООЬ".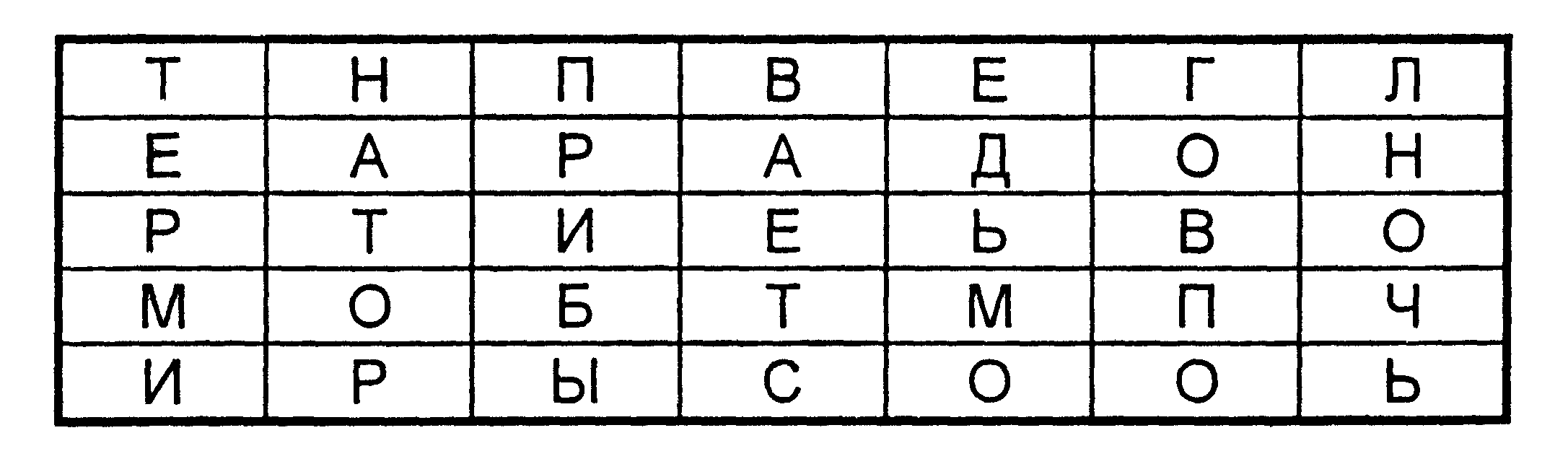


Рис. 1.3. Заполнение шифрующей таблицы из 5 строк и 7 столбцов

Естественно, отправитель и получатель сообщения должны заранее условиться об общем ключе в виде размера таблицы. Следует заметить, что объединение букв шифртекста в 5-буквенные группы не входит в ключ шифра и осуществляется для удобства записи несмыслового текста. При расшифровании действия выполняют в обратном порядке.

Несколько большей стойкостью к раскрытию обладает метод шифрования, называемый одиночной перестановкой по ключу. Этот метод отличается от предыдущего тем, что столбцы таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.

Применим в качестве ключа, например, слово "ПЕЛИКАН", а текст сообщения возьмем из предыдущего примера. На рис. 1.4 показаны две таблицы, заполненные текстом сообщения и ключевым словом, при этом левая таблица соответствует заполнению до перестановки, а правая таблица – заполнению после перестановки.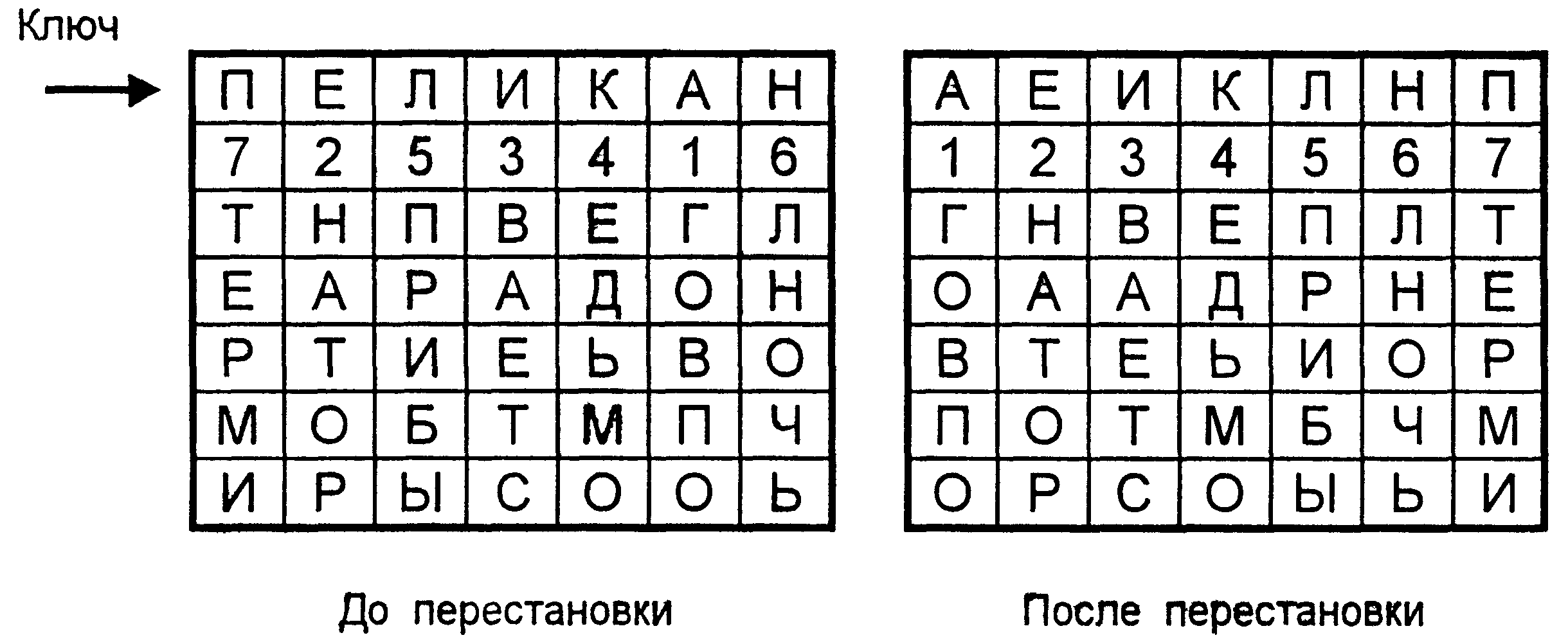


Рис. 1.4. Шифрующие таблицы, заполненные ключевым словом и текстом сообщения

В верхней строке левой таблицы записан ключ, а номера под буквами ключа определены в соответствии с естественным порядком соответствующих букв ключа в алфавите. Если бы в ключе встретились одинаковые буквы, они бы были понумерованы слева направо. В правой таблице столбцы переставлены в соответствии с упорядоченными номерами букв ключа.

При считывании содержимого правой таблицы по строкам и записи шифртекста группами по пять букв получим шифрованное сообщение: "ГНВЕП ЛТООА ДРНЕВ ТЕЬИО РПОТМ БЧМОР СОЫЬИ".

Для обеспечения дополнительной скрытности можно повторно зашифровать сообщение, которое уже прошло шифрование. Такой метод шифрования называется двойной перестановкой. В случае двойной перестановки столбцов и строк таблицы перестановки определяются отдельно для столбцов и отдельно для строк. Сначала в таблицу записывается текст сообщения, а потом поочередно переставляются столбцы, а затем строки. При расшифровании порядок перестановок должен быть обратным.

Пример выполнения шифрования методом двойной перестановки показан на рис. 1.5. Если считывать шифртекст из правой таблицы построчно блоками по четыре буквы, то получится следующее: "ТЮАЕ ООГМ РЛИП ОЬСВ".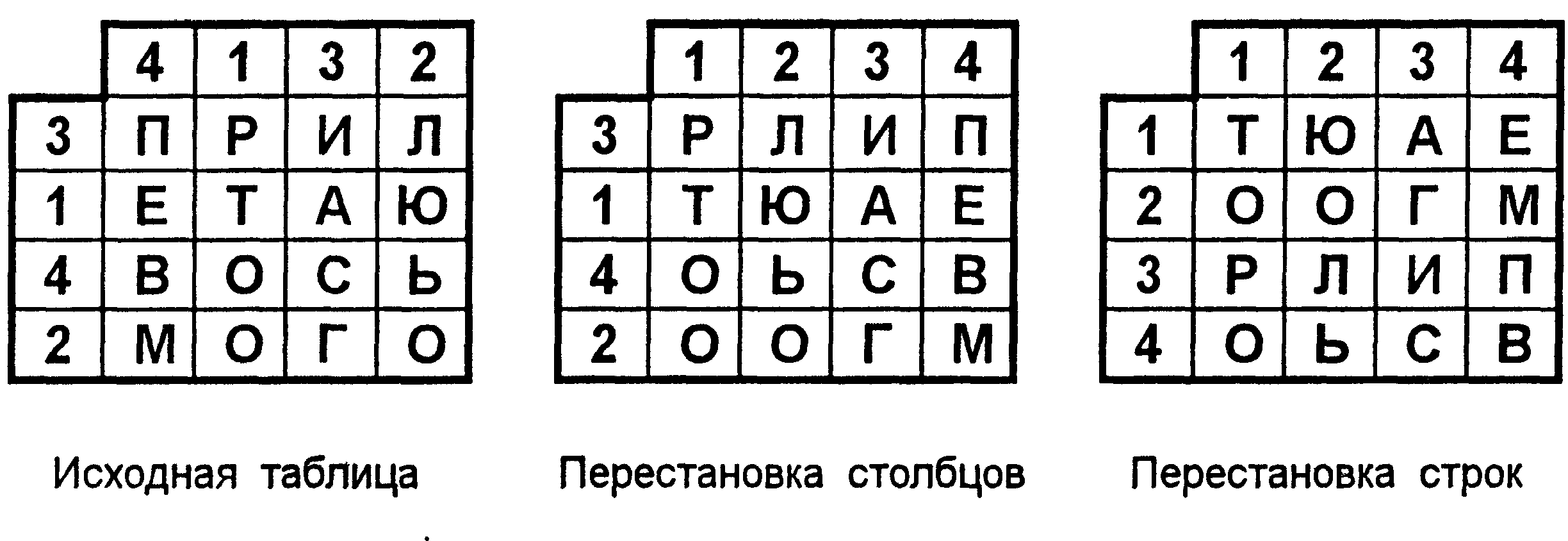


Рис. 1.5. Пример выполнения шифрования методом двойной перестановки

Ключом к шифру двойной перестановки служит последовательность номеров столбцов и номеров строк исходной таблицы (в нашем примере последовательности 4132 и 3142 соответственно).

Число вариантов двойной перестановки быстро возрастает при увеличении размера таблицы:

1. 
   для таблицы 3x3 36 вариантов;
   
2. 
   для таблицы 4x4 576 вариантов;
   
3. 
   для таблицы 5x5 14400 вариантов.
   

Шифрование с помощью магических квадратов. В средние века для шифрования перестановкой применялись и магические квадраты. Магическими квадратами называют квадратные таблицы с вписанными в их клетки последовательными натуральными числами, начиная от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.

Шифруемый текст вписывали в магические квадраты в соответствии с нумерацией их клеток. Если затем выписать содержимое такой таблицы по строкам, то получится шифртекст, сформированный благодаря перестановке букв исходного сообщения.

Пример магического квадрата и его заполнения сообщением "ПРИЛЕТАЮ ВОСЬМОГО" показан на рис. 1.6.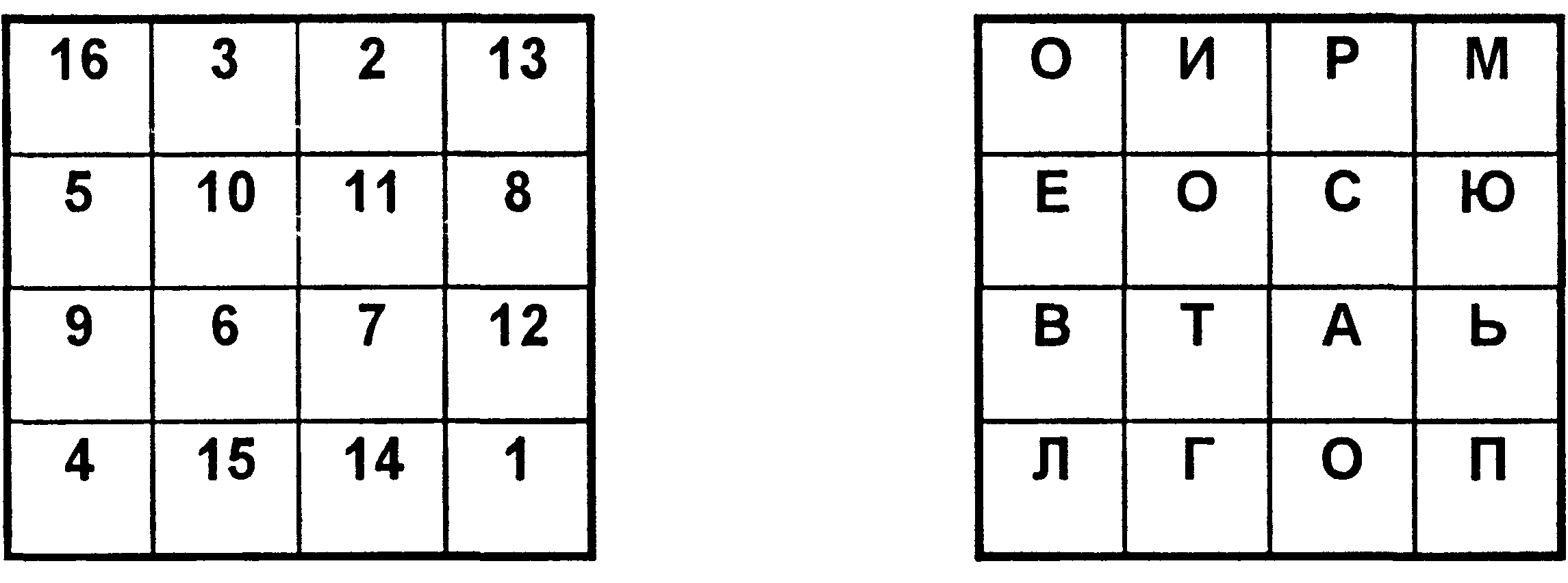


Рис. 1.6. Пример магического квадрата 4х4 и его заполнение сообщением

Шифртекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вполне загадочный вид: "ОИРМ ЕОСЮ ВТАЪ ЛГОП".

Число магических квадратов быстро возрастает с увеличением размера квадрата. Существует только один магический квадрат размером 3x3 (если не учитывать его повороты). Количество магических квадратов 4x4 составляет уже 880, а количество магических квадратов 5x5 – около 250000.

Магические квадраты средних и больших размеров могли служить хорошей базой для обеспечения нужд шифрования того времени, поскольку практически нереально выполнить вручную перебор всех вариантов для такого шифра.

Шифры замены

Шифрами замены называются такие шифры, преобразования из которых приводят к замене каждого символа открытого текста на другие символы – шифрообозначения, причем порядок следования шифрообозначений совпадает с порядком следования соответствующих им символов открытого сообщения.

В своей простейшей форме шифр замены может быть задан таблицей подстановки, устанавливающей соответствие между буквами двух алфавитов A_n и B_n: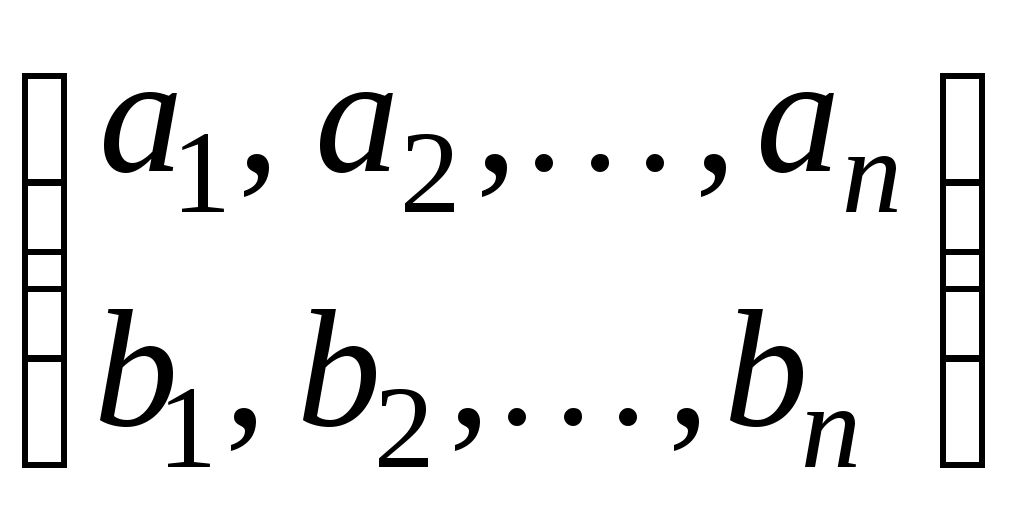

,

где – i-тая буква алфавита открытого текста, – шифрообозначение a_i (соответствующая a_i буква алфавита шифртекста).

В качестве примера преобразования, которое может содержаться в шифре замены, приведем такое правило. Каждая буква исходного сообщения заменяется на ее порядковый номер в алфавите. В этом случае исходный буквенный текст преобразуется в числовой.

Алфавиты A_n и B_nне обязательно должны быть различными. В практической криптографии очень часто применяются шифры, в которых алфавиты A_n и B_nсовпадают.

В шифре простой замены каждый символ исходного текста заменяется символами того же алфавита одинаково на всем протяжении текста.

В шифрах сложной замены для шифрования каждого символа открытого текста применяют свой шифр простой замены. Для реализации шифров сложной замены последовательно и циклически меняют используемые таблицы подстановки.

Полибианский квадрат. Одним из первых шифров простой замены считается так называемый полибианский квадрат. За два века до нашей эры греческий писатель и историк Полибий изобрел для целей шифрования квадратную таблицу размером 5x5, заполненную буквами греческого алфавита в случайном порядке (рис. 1.7).



Рис. 1.7. Полибианский квадрат

При шифровании в этом полибианском квадрате находили очередную букву открытого текста и записывали в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывалась в нижней строке таблицы, то для шифртекста брали самую верхнюю букву из того же столбца. Например, для слова "" получается шифртекст "".

Концепция полибианского квадрата оказалась плодотворной и нашла применение в криптосистемах последующего времени.

Система шифрования Цезаря. Шифр Цезаря является частным случаем шифра простой замены. Свое название этот шифр получил по имени римского императора Гая Юлия Цезаря, который использовал этот шифр при переписке с Цицероном (около 50 г. до н.э.).

При шифровании исходного текста каждая буква заменялась на другую букву того же алфавита по следующему правилу. Заменяющая буква определялась путем смещения по алфавиту от исходной буквы на К букв. При достижении конца алфавита выполнялся циклический переход к его началу. Цезарь использовал шифр замены при смещении К = 3. Такой шифр замены можно задать таблицей подстановки, содержащей соответствующие пары букв открытого текста и шифртекста. Совокупность возможных подстановок для К=3 показана в табл. 1.1.

Таблица 1.1.

Таблица подстановкИ шифра Цезаря

AD JM SV

BE KN TW

CF LO UX

DG MP VY

EH NQ WZ

FI OR XA

GJ PS YB

HK QT ZC

IL RU

Например, послание Цезаря "VENI VIDI VICI" ("Пришел, Увидел, Победил") выглядело бы в зашифрованном виде так: "YHQL YLGL YLFL".

Система шифрования Цезаря с ключевым словом. Особенностью этой системы является использование ключевого слова для смещения и изменения порядка символов в алфавите подстановки.

Выберем некоторое число k, 0 < k < 25 , и слово или короткую фразу в качестве ключевого слова. Желательно, чтобы все буквы ключевого слова были различными. Пусть выбраны слово DIPLOMAT в качестве ключевого слова и число k = 5.

Ключевое слово записывается под буквами алфавита, начиная с буквы, числовой код которой совпадает с выбранным числом k:

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
					D	I	P	L	O	M	A	T

Оставшиеся буквы алфавита подстановки записываются после ключевого слова в алфавитном порядке:

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

V

W

X

Y

Z

D

I

P

L

O

M

A

T

B

C

E

F

G

H

J

K

N

Q

R

S

U

Теперь мы имеем подстановку для каждой буквы произвольного сообщения. Исходное сообщение "SEND MORE MONEY" шифруется как "HZBY TCGZ TCBZS".

Следует отметить, что требование о различии всех букв ключевого слова не обязательно. Можно просто записать ключевое слово (или фразу) без повторения одинаковых букв.

Шифрующие таблицы Трисемуса. В 1508 г. аббат из Германии Иоганн Трисемус написал печатную работу по криптологии под названием "Полиграфия". В этой книге он впервые систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра замены обычно использовались таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку. Поскольку ключевое слово или фразу легко хранить в памяти, то такой подход упрощал процессы шифрования и расшифрования.

Поясним этот метод шифрования на примере. Для русского алфавита шифрующая таблица может иметь размер 4x8. Выберем в качестве ключа слово БАНДЕРОЛЬ. Шифрующая таблица с таким ключом показана на рис. 1.8.

Б	А	Н	Д	Е	Р	О	Л
Ь	В	Г	Ж	З	И	Й	К
М	П	С	Т	У	Ф	Х	Ц
Ч	Ш	Щ	Ы	Ъ	Э	Ю	Я

Рис. 1.8. Шифрующая таблица Трисемуса с ключевым словом "БАНДЕРОЛЬ"

Как и в случае полибианского квадрата, при шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самую верхнюю букву из того же столбца.

Например, при шифровании с помощью этой таблицы сообщения "ВЫЛЕТАЕМПЯТОГО" получаем шифртекст "ПДКЗЫВЗЧШЛЫЙСЙ".

Система шифрования Вижинера впервые была опубликована в 1586 г. и является одной из старейших и наиболее известных шифров сложной замены. Свое название она получила по имени французского дипломата XVI века Блеза Вижинера, который развивал и совершенствовал криптографические системы.

Система Вижинера подобна такой системе шифрования Цезаря, у которой ключ подстановки меняется от буквы к букве. Этот шифр можно описать таблицей шифрования, называемой таблицей (квадратом) Вижинера. Пример квадрата Вижинера для русского языка приведен в табл. 1.2.

Таблица Вижинера используется для шифрования и расшифрования. Таблица имеет два входа: верхнюю строку подчеркнутых символов, используемую для считывания очередной буквы исходного открытого текста; крайний левый столбец ключа. Последовательность ключей обычно получают из числовых значений букв ключевого слова.

При шифровании исходного сообщения его выписывают в строку, а под ним записывают ключевое слово (или фразу). Если ключ оказался короче сообщения, то его циклически повторяют. В процессе шифрования находят в верхней строке таблицы очередную букву исходного текста и в левом столбце очередное значение ключа. Очередная буква шифртекста находится на пересечении столбца, определяемого шифруемой буквой, и строки, определяемой числовым значением ключа.

Рассмотрим пример получения шифртекста с помощью таблицы Вижинера. Пусть выбрано ключевое слово "АМБРОЗИЯ". Необходимо зашифровать сообщение "ПРИЛЕТАЮ СЕДЬМОГО".

Выпишем исходное сообщение в строку и запишем под ним ключевое слово с повторением. В третью строку будем выписывать буквы шифртекста, определяемые из таблицы Вижинера.

Сообщение ПРИЛЕТАЮ СЕДЬМОГО

Ключ АМБРОЗИЯ АМБРОЗИЯ

Шифртекст ПЪЙЫУЩИЭ ССЕКЬХЛН

Таблица 1.2.

Квадрат Вижиненра для русского языка

Содержание работы

1. 
   В соответствии со своим вариантом разработать программы для шифрования и расшифровывания русскоязычного текста при помощи шифра перестановки и шифра замены. Программы должны обеспечивать:
   

• 
  шифрование информации, находящейся в текстовом файле, с записью результата в другой файл;
  
• 
  шифрование информации, вводимой с клавиатуры, с записью в файл только зашифрованного текста;
  
• 
  ввод ключа шифрования/расшифрования с клавиатуры без отображения его на экране;
  
• 
  расшифровку текста, содержащегося в файле, с выводом результатов на экран или в другой файл (ключ расшифровывания вводится с клавиатуры без эха).
  

2. 
   При помощи созданной программы подготовить зашифрованный русский текст объемом не менее 2000 символов.
   

Варианты заданий

№ варианта	Шифры
1	Шифр скитала, шифр Трисемуса
2	Шифр скитала, шифр Цезаря
3	Шифр скитала, шифр Цезаря с ключевым словом
4	Шифр скитала, шифр Вижиненра
5	Простая шифрующая таблица, шифр Трисемуса
6	Простая шифрующая таблица перестановки, шифр Цезаря
7	Простая шифрующая таблица перестановки, шифр Цезаря с ключевым словом
8	Простая шифрующая таблица перестановки, шифр Вижиненра
9	Одиночная перестановка по ключу, шифр Трисемуса
10	Одиночная перестановка по ключу, шифр Цезаря
11	Одиночная перестановка по ключу, шифр Цезаря с ключевым словом
12	Одиночная перестановка по ключу, шифр Вижиненра
13	Двойная перестановка по ключу, шифр Трисемуса
14	Двойная перестановка по ключу, шифр Цезаря
15	Двойная перестановка по ключу, шифр Цезаря с ключевым словом
16	Двойная перестановка по ключу, шифр Вижиненра

Содержание отчета

1. 
   Номер и тема лабораторной работы
   
2. 
   Описание и тексты программ.
   
3. 
   Исходный и зашифрованный текст.