Ассиметричное шифрование. АсиметричноеШифроавниеПростымиСловами. Асимметричное шифрование. Как это работает
 Скачать 184.81 Kb.
|
|
Асимметричное шифрование. Как это работает? 177 комментариев  Мало кто знает как именно работает асимметричное шифрование. К примеру есть люди которые не считают протокол https какой-либо адекватной защитой передаваемых данных. И как правило на попытку убедить в обратном, они отвечают что-то в духе «если мы передаем зашифрованные данные, то мы должны сказать как их расшифровывать, а эту информацию можно перехватить и, следовательно, расшифровать данные». А на аргументы, что это не так и в основу положено асимметричное шифрование, поступает ответ «Ну и что?».Ладно, я понимаю, знать все тонкости реализации асимметричного шифрования нужно далеко не всем. Но общий принцип работы, я считаю, должен знать каждый, кто как-либо связан с компьютерами. Хочу вынести суть данного поста в эту аннотацию: Запомните, асимметричное шифрование безопасно, естественно при выполнении всех условий. И чтобы доказать это я попробую описать алгоритм понятным языком, чтобы каждый смог понять, что он безопасен. Встречайте Алису, Боба и Еву и передачу их секретного сообщения под катом. Кстати почему Алиса и Боб? Об этом есть кратенькая статья на википедии: Алиса, Боб и Ева. Чтобы было понятнее, Алиса и Боб хотят обменяться сообщениями, а Ева пытается эти сообщения перехватить и прочесть. Прошу прощения за этот назойливый блок рекламы... ...ей я лишь пытаюсь окупить хостинг :) больше не показывать Немного истории Криптография прошлых веков имела одну огромную проблему — проблема передачи ключей. В те времена существовали только так называемые «симметричные» шифры — шифры при котором данные шифруются и расшифровываются одним и тем же ключом. К примеру, Алиса зашифровала некоторое сообщение и хочет отправить его Бобу. Естественно, чтобы Боб его прочитал, ему нужен ключ которым было зашифровано данное сообщение. И тут возникает проблема, как передать ключ чтобы его никто не смог перехватить. Пытливые умы предложат — пусть передают при личной встрече, а потом общаются сколько захотят. Да, не спорю, выход. А теперь представьте на секунду, что ваша интернет почта, перед тем как вы авторизируетесь в ней, потребует вашей поездки до физического местоположения сервера с почтой. Удобно? Пожалуй не очень. Конечно ключ можно передавать по другому каналу связи. Но криптография рассматривает все незащищенные каналы связи как небезопасные. То есть передача ключа Бобу по телефону, например, считается небезопасной так, как ничто не мешает Еве прослушивать и телефон в том числе. До 70-ых годов, эта проблема настолько стала привычной, что считался аксиомой тот факт, что для передачи сообщения нужно передавать и ключ которым сообщение зашифровано (причем некоторых люди до сих пор считают именно так). Но в 76 году Диффи и Хеллман предложили свой «метод экспоненциального обмена ключей». С этих годов и началось развитие асимметричных криптосистем. Немножко реальной жизни Прежде чем изучать какой либо алгоритм, нужно представить как он работает. И самый простой способ — это сравнить его с работой чего-то в реальности. Представим что Алиса и Боб живут в стране, в которой вся почтовая система абсолютно аморальна и почтовые служащие читают всю незащищенную корреспонденцию. Алиса, девочка не глупая, прежде чем отправить сообщение Бобу, взяла железный ящик и, положив внутрь письмо и закрыв его на свой замок, отправляет этот ящик Бобу. Естественно на почте прочитать это письмо не могут, но его не может прочитать и сам Боб, так как у него нет ключа которым закрыт замок. Алиса, конечно, может взять еще один железный ящик, положить в него ключ от предыдущего, и отправить его Бобу, но его Боб тоже не сможет открыть… Единственный путь это все же сделать дубликат ключа и дать его Бобу при личной встрече… И вот начинает казаться что обмен ключами является неизбежной частью шифрования — или все-таки нет? Представим другую картину. Распишу пошагово: Алиса кладет свое письмо в железный ящик и, заперев его на замок, отправляет Бобу. Боб при получении ящика, (внимание!) берет свой замок и, дополнительно заперев им ящик, отправляет обратно. Алисе ящик приходит уже с двумя замками (напомню с первым замком Алисы от которого у нее есть ключ, и со вторым — Боба, от которого ключ есть есть только у Боба). Алиса снимает свой замок, и отправляет ящик обратно Бобу Бобу приходит ящик с уже одним его замком от которого у него есть ключ Боб отпирает оставшийся его замок своим ключом, и читает сообщение Значение этой кратенькой истории огромно. Она показывает что два человека могут передавать секретное сообщение без обмена ключами. Вдумайтесь! Эта история фактически рушит все аксиомы на которых была построена тогдашняя криптография. Да мы получаем некоторое усложнение процесса (ящик пришлось пересылать три раза), но результат… Вернемся к криптографии Казалось бы решение найдено. Отправитель и принимающий шифруют свое сообщение, и затем собеседники поочередно снимают свой шифр. 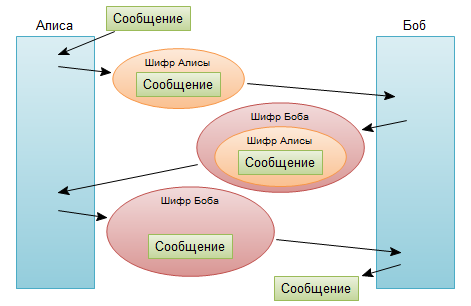 Но суть в том что не существуют таких шифров, которые бы позволили снять шифр из под другого шифра. То есть этап где Алиса снимает свой шифр невозможен: 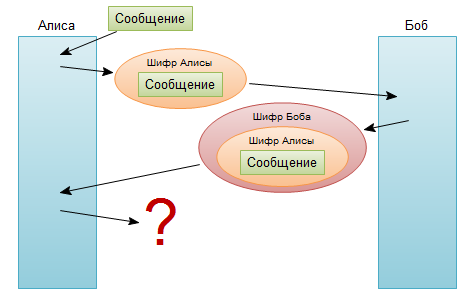 К сожалению, все имеющиеся алгоритмы до сих пор требуют снятия шифров в той очереди в которой они были применены. Боюсь назвать это аксиомой (так как история уже знает случаи когда такие аксиомы разбивались в пух и прах), но это так до сих пор. Вернемся к математике Идея с ящиком, о которой я описывал выше, вдохновили Диффи и Хеллмана искать способ передачи сообщения. В конце концов они пришли к использованию односторонних функций. Что такое односторонняя функция? К примеру есть функция удвоение, т.е удвоить(4)=8, она двухсторонняя, т.к. из результата 8 легко получить исходное значение 4. Односторонняя функция — та функция после применения которой практически невозможно получить исходное значение. К примеру смешивание желтой и синей краски — пример односторонней функции. Смешать их легко, а вот получить обратно исходные компоненты — невозможно. Одна из таких функций в математике — вычисление по модулю. За основу алгоритма Хеллман предложил функцию Yx (mod P). Обратное преобразование для такой функции очень сложно, и можно сказать что, по сути, заключается в полном переборе исходных значений. К примеру вам сказали, что 5 x (mod 7) = 2, попробуйте найдите x, а? Нашли? А теперь представьте что за Y и P взяты числа порядка 10300. Кстати сказать, для повышения стойкости, число P должно являться простым числом, а Y — являться первообразным корнем по модулю P. Но так как мы все же пытаемся понять теорию, то смысла заморачиваться на этом я не вижу. Алгоритм Диффи-Хеллмана И вот однажды Хеллмана осенило и он смог разработать рабочий алгоритм обмена ключами. Для работы по этому алгоритму нужно выполнять шаги на обоих сторонах, поэтому я зарисую это в таблице:
Магия? Не спорю, с первого взгляда непонятно. Но после вчитывания и вдумывания в эту таблицу становится понятно как это работает. Впрочем если понятно не стало, то пролистайте до конца главы, там я выложил поясняющее видео. Причем обратите внимание, что для получения ключа в конечной формуле, любому человеку нужно иметь три значения: Значения a и P, и секретное число Боба B или значения b и P, и секретное число Алисы A Но секретные числа по каналу не передаются! Еве не получится восстановить ключ, не имея чьего-нибудь секретного числа. Почему — я писал выше, данная функция является односторонней. Попробуйте решите уравнение 4x (mod 11) = 2y (mod 11) найдя x и y. Чтобы было понятнее, как работает схема Хеллмана, представьте шифр, в котором в качестве ключа каким-то образом используется цвет: Допустим вначале, что у всех, включая Алису, Боба и Еву, имеется трехлитровая банка, в которую налит один литр желтой краски. Если Алиса и Боб хотят договориться о секретном ключе, они добавляют в свои банки по одному литру своей собственной секретной краски. Алиса может добавить краску фиолетового оттенка, а Боб — малинового. После этого каждый из них посылает свою банку с перемешанным содержимым другому. И наконец, Алиса берет смесь Боба и подливает в нее один литр своей секретной краски, а Боб берет смесь Алисы и добавляет в нее один литр своей секретной краски. Краска в обеих банках теперь станет одного цвета, поскольку в каждой находится по одному литру желтой, фиолетовой и малиновой краски. Именно этот цвет, полученный при добавлении дважды в банки красок, и будет использоваться как ключ. Алиса понятия не имеет, какую краску добавил Боб, а Боб также не представляет, какую краску налила Алиса, но оба они достигли одного и того же результата. Между тем Ева в ярости. Даже если она и сумеет перехватить банки с промежуточным продуктом, ей не удастся определить конечный цвет, который и будет согласованным ключом. Ева может видеть цвет краски, полученной при перемешивании желтой краски и секретной краски Алисы в банке, отправленной Бобу, и она может видеть цвет краски, полученной при перемешивании желтой краски и секретной краски Боба в банке, отправленной Алисе, но чтобы найти ключ, ей, на самом деле, необходимо знать цвета исходных секретных красок Алисы и Боба. Однако, рассматривая банки с перемешанными красками, Ева не сможет определить секретные краски Алисы и Боба. Даже если она возьмет образец одной из смешанных красок, ей не удастся разделить ее на исходные краски, чтобы найти секретную, поскольку смешивание краски является односторонней функцией. Все равно непонятно? Тогда смотрим видео: Что же, надеюсь, вы поняли, что существует вполне реальный способ безопасного обмена ключами. Но прошу заметить, назвать этот алгоритм асимметричным шифром пока нельзя, так как по сути это всего лишь алгоритм обмена ключами. Асимметричное шифрование асимметричный алгоритм предполагает под собой наличие двух ключей — публичного и приватного. То есть сообщение шифруется публичным ключом, а расшифровывается приватным и ни как иначе. Собственно именно эту концепцию сформулировал Диффи. В общем суть данного алгоритма заключается в том, что принимающая сторона перед приемкой сообщения генерирует пару ключей на основе алгоритма модульной арифметики (принцип такой же как и в алгоритме Диффи-Хеллмана), собственно приватный и публичный ключ. Отправитель перед отправкой получает публичный ключ и шифрует сообщение данным ключом, после чего данное сообщение можно расшифровать только приватным ключом, который хранится в секрете у принимающей стороны. 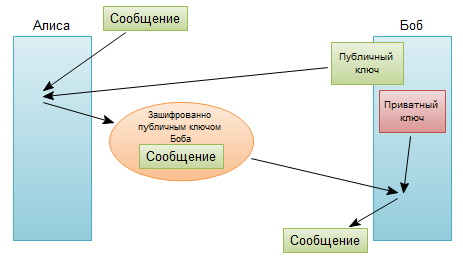 Если вернуться к аналогии с замками, то шифрование с открытым ключом можно представить себе следующим образом: Любой способен запереть замок, просто защелкнув его, чтобы он закрылся, но отпереть его может только тот, у кого есть ключ. Запереть замок (зашифровывание) легко, почти все могут это сделать, но открыть его (расшифровывание) имеет возможность только владелец ключа. Понимание того, как защелкнуть замок, чтобы он закрылся, ничего не скажет вам, как его отпереть. Можно провести и более глубокую аналогию. Представьте, что Алиса проектирует замок и ключ. Она бдительно охраняет ключ, но при этом изготавливает тысячи дубликатов замков и рассылает их по почтовым отделениям по всему миру. Если Боб хочет послать сообщение, он кладет его в коробку, идет на местный почтамт, просит «замок Алисы» и запирает им коробку. Теперь уже ему не удастся открыть коробку, но когда коробку получит Алиса, она сможет открыть ее своим единственным ключом. Замок и защелкивание его, чтобы он закрылся, эквивалентны общему ключу для зашифровывания, поскольку все имеют доступ к замкам и все могут воспользоваться замком, чтобы закрыть сообщение в коробке. Ключ от замка эквивалентен секретному ключу для расшифровывания, потому что он имеется только у Алисы, только она сможет открыть замок, и только она сможет получить доступ к находящемуся в коробке сообщению. Есть несколько алгоритмов реализующих асимметричное шифрование. Самый известный из них — RSA. Расписывать его я не вижу смысла, так как понять как он работает с ходу все равно не получится, да и лучше чем написано на википедии я написать все равно не смогу. Заключение Что же, надеюсь что, поняв как работает асимметричное шифрование изнутри, вы станете больше ему доверять и соответственно чаще пользоваться SSL =) Использовались материалы из книги Сингх Саймон — Книга шифров. Кстати, самая лучшая книга для тех кто хочет хотя бы чуточку разбираться в криптографии. Всем советую прочитать. Позволю себе вставить ссылку на один из прошлых моих постов: Коллизии хеш функций? асимметричное шифрование решает! — пример «нестандартного» применения асимметричного шифрования. | |||||||||||||||||||||