урок алгебры экологии в 8классе Решение задач с помощью квадратных уравнений. 8 класс реш задач кв ур. Решение задач с помощью квадратного уравнения
 Скачать 131.35 Kb. Скачать 131.35 Kb.
|
|
Урок алгебры в 8 классе Тема: решение задач с помощью квадратного уравнения Цели: уметь составлять квадратные уравнения для решения текстовых алгебраических, геометрических и физических задач, которые встречаются в жизни; уметь решать квадратные уравнения по формуле; проверить, может ли математика помочь в решении экологических проблем; через математику и экологию формировать позитивное отношение к окружающей среде. Ход урока Организационный момент. Добрый день, дорогие друзья! Многие ребята спрашивают: «Зачем мне нужна математика? В жизни эти формулы и уравнения не пригодятся!» Я хочу в очередной раз убедить вас, ребята, в обратном! Сегодня для всех нас очень важна тема - охрана природы. Охраняется Красною книгой Столько редких животных и птиц, Чтобы выжил простор многоликий Ради света грядущих зарниц. Чтоб пустыни нагрянуть не смели, Чтобы души не стали пусты Охраняются звери, Охраняются змеи, Охраняются даже цветы. Ни лес, ни река, ни озера, ни луга не могут сами позаботиться о себе. Не могут защитить себя ни птицы, ни насекомые, ни мелкие звери. Первое, с чего начинается дружба с природой, будет то, что вы не принесете ей вреда! Мы отправимся с вами в заказник с. Теплоключенка. Но сначала вспомним, какую тему изучали на прошлом уроке? Да! «Решение задач с помощью квадратного уравнения» Давайте вспомним алгоритм решения квадратного уравнения в общем виде. II. Устная работа. Алгоритм решения квадратного уравнения в общем виде ax2 + bx + c = 0, a ≠ 0. D = b2 – 4ac – дискриминант. Возможны три случая. 1. D = b2 – 4ac < 0 - уравнение не имеет действительных корней. 2. D = b2 – 4ac = 0 - квадратное уравнение имеет один корень. 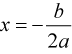 3. D = b2 – 4ac > 0 - квадратное уравнение имеет два корня: 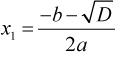 или или 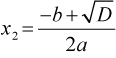 . .На прошлом уроке мы узнали, что многие задачи алгебры, приводят к необходимости решения квадратного уравнения. Давайте вспомним алгоритм решения задачи с помощью квадратного уравнения. Этапы решения задачи алгебраическим методом: 1. Выбрать неизвестное. 2. Затем составить уравнение. 3. Решить его. 4. Сделать вывод о корнях. 5. Выполнить дополнительные действия. Выполнение заданий Мы отправляемся с вами в заказник с. Теплоключенка. Теплоключенский охотничий заказник был сформирован в 1958 году на северном склоне Тескей Ала-Тоо в бассейне реки Алтын Арашан с целью сохранения животных и защиты естественных горных лесов. И до сих пор занимает площадь порядка 29 тыс. га в живописном бассейне реки Арашан. Эти места издавна были знамениты тем, что здесь обитает редкий вид животного – снежный барс, и заказник был создан с целью охраны этого вида животного. Задача1: Площадь части заповедной зоны, где обитает редкий вид животного- снежный барс, имеющей форму прямоугольника, одна сторона которой на 6 км больше другой, равна 187 кв.км. Сколько нужно приобрести сетки для забора? Разбор задачи. Какую форму имеет заповедник? Прямоугольную Что известно о его сторонах? Одна сторона на 6 км больше другой Что ещё известно в задаче? Площадь Что надо найти? Сколько нужно приобрести сетки для забора? Что это значит? Надо найти периметр прямоугольника по формуле: P=(a+ b)·2 Решение: Пусть меньшая сторона х км, тогда другая сторона (х+6) км. Известно, что площадь заповедника равна 187 кв. км. Составлю и решу уравнение: х(х+6)=187 х2+6х-187=0 a= 1, k=3, c= -187 D1=k2–ac= 9-(-187)= 196, D1>0, √ D1 =14 x1 = (-3-14):1= -17 – не удовлетворяет условию задачи, т.к. длина положительная величина. х2=(-3+14):1=11 11 км длина одной стороны забора. 11+6=17(км)- длина второй стороны забора. (11+17)·2= 56 (км)- длина забора. Значит, для забора нужно купить 56 км сетки. Ответ: 56 км. Задача 2. Шишку бросили вертикально вверх с начальной скоростью 40 м/с. Через сколько секунд она окажется на высоте 60 м? Решение. Анализ условия. Из курса физики известно, что, если не учитывать сопротивление воздуха, то высота h(м), на которой брошенная вертикально вверх шишка окажется через t(c), может быть найдена по формуле h=V0 t-gt2/2, где Vo(м/с)-начальная скорость, g-ускорение свободного падения, приближенно равное 10 м/с2. Определенной высоты шишка может достигнуть дважды: при взлете и при падении вниз. Дано: Vo = 40м/с h = 60 м g = 10 м/с2 Найти: t Пусть t (c) неизвестное время полета шишки до необходимой высоты. Тогда, подставив значения h и Vo в формулу, получим 60=40t-5t2. Составлю и решу уравнение: 5t2-40t+60=0 (:5) t2-8t+12=0 a= 1, k= -4, c= 12 D1=k2–ac= 16-12= 4, D1>0, √ D1 = 2 t1= (-k - √ D1): a=4-2=2; t2= = (-k + √ D1): a=4 + 2=6. Шишка, брошенная вертикально вверх, окажется на высоте 60 м от земли дважды: через 2 с и через 6 с после бросания. Условию задачи удовлетворяют оба найденных корня. Ответ: на высоте 60 м тело окажется через 2 с и через 6 с. Задача 3. Часто для прогулки в горы мы берём с собой чипсы. Мне захотелось вычислить, какую площадь земли можно покрыть пакетами из-под чипсов, если одна из сторон пакета на 14 см больше другой, а диагональ равна 34 см. Какую площадь земли можно покрыть пакетами из-под чипсов за 4 дня семьёй из 5 человек, если в походе каждый съедает по 2 пачки чипсов. Анализ условия. Какую форму имеет упаковка? Прямоугольную Что известно в задаче? Одна сторона на 14 см больше другой, диагональ равна 34 см. Это значит, что мы будем работать со сторонами прямоугольного треугольника, т.к. диагональ делит прямоугольник на два прямоугольных треугольника Что надо найти? Какую площадь земли можно покрыть пакетами из-под чипсов за 4 дня. Как найдём? Сначала найдём площадь одного пакета. Затем сколько упаковок чипсов съедает семья за 4 дня, и общую площадь упаковок. Решение. Пусть одна сторона упаковки х см, тогда вторая (х+14) см. известна диагональ упаковки – 34 см. Пользуясь теоремой Пифагора, составлю и решу уравнение: Х2 +(х+14)2 = 342 х2 + х2 +28х + 196 – 1156 = 0 2 х2 + 28х – 960 = 0 (:2) х2 + 14х – 480 = 0 a=1, b=14, c=-480 D=b2–4ac = 196 +4·480 = 196 + 1920=2116, √D = 46 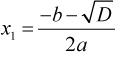 или или х1= 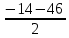 = -30 – не удовлетворяет условию задачи, т.к. длина положительная величина. = -30 – не удовлетворяет условию задачи, т.к. длина положительная величина.х2= 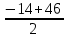 =16 =1616 см- длина одной стороны. 16+14=30 (см)- длина второй стороны. 16·30= 480 (см2) – площадь упаковки. Т.к. семья состоит из 5 человек и в походе каждый съедает по 2 пачки чипсов, то 5·2=10 (пач.) - съедают вместе за 1 день 4·10= 40 (пач.) - съедают вместе за 4 дня 480·40= 19 200 (см2)- площадь всех упаковок 19 200 см2 =1,92 м2 ≈ 2 м2 земли можно покрыть пакетами из-под чипсов! Представьте теперь, какую площадь земли засорят несколько семей каждые выходные! Ни птицам, ни насекомым, ни мелким зверям, ни растениям не останется места в лесу! Итог урока. С чего начать? С самого простого. Увидели в лесу или на берегу реки мусор - уберите его, закопайте в землю там, где можно, аккуратно сожгите то, что горит. Не ломайте веток, а тем более верхушек у молодых деревьев. Не вытаптывайте молодую поросль. Берегите птиц, муравьев! Я думаю, что этот урок сегодня убедил вас в том, что математика с её формулами НУЖНА И ПРИМЕНЯЕТСЯ В ЖИЗНИ! Моё предположение о том, что математика напрямую связана с экологией, подтвердилось. При изучении экологии возникает много вопросов, ответы на которые можно получить при помощи математики. На основе математических вычислений, люди делают выводы о том, какую пользу или вред мы наносим природе, а значит и нашему будущему. Математика позволяет проводить точные измерения, делать расчёты и подтверждать наблюдения. Текстовые задачи имеют возможность для раскрытия вопросов о среде обитания, заботы о ней, рациональном природопользовании, восстановлении и приумножении ее природных богатств. Домашнее задание: решите задачу. Задача 4. Цветок лотоса возвышался над тихим озером на полфута. Когда порыв ветра отклонил цветок от прежнего места на 2 фута, цветок скрылся под водой. Определите глубину озера. Решение. Анализ задачи. Пусть отрезки АВ и АD изображают лотос в двух положениях. Точка А на дне, а точка C на поверхности озера. Получается прямоугольный треугольник ABC. 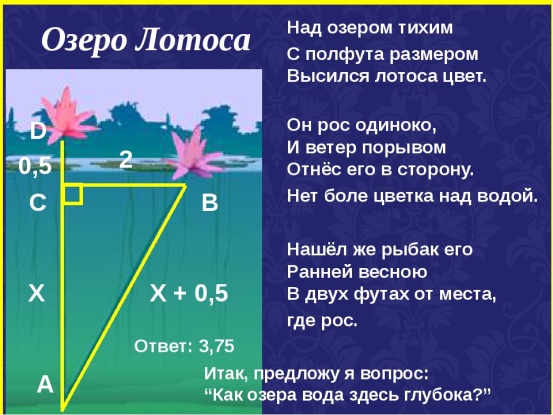 Пусть глубина озера АC = х футов. Тогда высота цветка лотоса над уровнем водоема CD = ½ фута, значит, длина стебля АD= AD=х+1/2 фута. По теореме Пифагора составим уравнение х2 + 22 = (х + 1/2)2 Решим уравнение х2 + 22 = х2 +21/2х + (1/2)2 х2 + 4 - х2 –х -1/4 =0 х=3 ¾ (фута) – глубина озера. Получили реальный результат, являющийся ответом на главный вопрос задачи. Ответ: глубина озера 3 ¾ фута. |
