Лабораторная работа №1 Решение логических задач. Лабораторная работа 1 Решение логических задач Цель работы

• Название: Лабораторная работа 1 Решение логических задач Цель работы
• Дата: 06.12.2021
• Размер: 454.13 Kb.
• Имя файла: Лабораторная работа №1 Решение логических задач.docx
• Тип: Лабораторная работа; #293179
• страница: 12 из 21

Контрольный пример 1

Андрей является торговым агентом компании VOLVO и занимается продажей последней модели этой марки автомобиля.

Годовой спрос оценивается в 4000 ед. Цена каждого автомобиля равна 90 млн. р., а годовые издержки хранения составляют 10% от цены самого автомобиля.

Андрей произвел анализ издержек заказа и понял, что средние издержки заказа составляют 25 млн. р. на заказ. Время выполнения заказа равно восьми дням. В течение этого времени ежедневный спрос на автомобили равен 20.

Необходимо в процессе решения данного примера ответить на следующие вопросы:

1. Чему равен оптимальный размер заказа?

2. Чему равна точка восстановления?

3. Каковы совокупные издержки?

4. Каково оптимальное количество заказов в год?

5. Каково оптимальное время между двумя заказами, если предположить, что количество рабочих дней в году равно 200?

Ниже приведено описание исходных данных и результаты решения контрольного примера с использованием условных обозначений:

Исходные данные:

величина спроса за год D=4000;

издержки заказа К = 25;

издержки хранения = 9/200;

цена за единицу с = 90;

время выполнения заказа L=8;

ежедневный спрос d= 20;

число рабочих дней Т = 200.

Решение:

оптимальный размер заказа Q* = 149;

точка восстановления R = 160 - 149 = 11;

число заказов за год N = 26,83;

совокупные издержки С = 1341;

стоимость продаж = 360000;

число дней между заказами t = 7,45.
Модель 3 оптимального размера заказа в предположении, что допускается дефицит продукта и связанная с ним упущенная прибыль (рис. 6.3).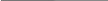

Рис.6.3. Модель 3

Пусть р - упущенная прибыль в единицу времени, возникающая в результате дефицита одной единицы продукта; Р - упущенная прибыль за период, возникающая в результате дефицита одной единицы продукта.

Тогда:Q* = (2dK/h)^1/2 x ((р+h)/р)^1/2=(2DK/H)^1/2 х ((Р+Н)/P)^1/2 - оптимальный размер заказа; S* = (2dK/h)^1/2 x (р/(h+р))^1/2 =(2DK/H)^1/2 x (P/(H+P))^1/2 - максимальный размер запаса; R = Q*- S* - максимальный дефицит.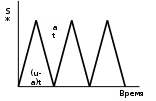

Модель.4 производства и распределения. В предыдущей модели мы допускали, что пополнение запаса происходит единовременно. Но в некоторых случаях, особенно в промышленном производстве, для комплектования партии товаров требуется значительное время и производство товаров для пополнения запасов происходит одновременно с удовлетворением спроса. Такой случай показан на рис.6.4.

Рис. 6.4. Модель 4

Спрос и производство являются частью цикла восстановления запасов. Пусть u - уровень производства в единицу времени, К - фиксированные издержки производства.

Тогда:

совокупные издержки хранения = (средний уровень запасов) х Н = Q/2[1-d/u] Н;

средний уровень запасов = (максимальный уровень запасов)/2;

максимальный уровень запасов = u t - d t = Q(l - d/u);

время выполнения заказа t = Q/u;

издержки заказа = (D/Q) К;

оптимальный размер заказа Q* = (2dK/h [(l-(d/u)])^1/2 = (2DK/H[(l-(d/u)])^1/2;

максимальный уровень запасов S* = Q*[(l-(d/u)].
Модель 5. Модель с количественными скидками. Для увеличения объема продаж компании часто предлагают количественные скидки своим покупателям.

Количественная скидка - сокращенная цена на товар в случае покупки большого количества этого товара. Ти­пичные примеры количественных скидок приведены в табл.8.1.

Таблица 6.1

Варианты скидок	1	2	3
Количество, при котором делается скидка	от 0 до 999	от 1000 до 1999	от 2000 и выше
Размер скидки, %	0	3	5
Цена со скидкой	5	4,8	4,75

Пусть I - доля издержек хранения в цене продукта с.

Тогда h = (I x c) и Q* = ( 2dK/(I x c))^1/2 - оптимальный размер заказа.