Лабораторная работа№1 (1). Лабораторная работа 1. Решение задач оптимизации в Excel Пример 1
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Лабораторная работа №1. Решение задач оптимизации в Excel Пример №1 Цех выпускает детали А и В. На производство детали А рабочий тратит 3 часа, на производство детали В - 2 часа. От реализации детали А предприятие получает прибыль 80 ден. ед., В - 60 ден. ед. Цех должен выпустить не менее 100 штук деталей А и не менее 200 штук деталей В. Сколько деталей каждого вида надо выпустить для получения наибольшей прибыли, если фонд рабочего времени составляет 900 человеко-часов. Математическая модель задачи Обозначим за x1 и x2 количество изделий А и В в оптимальном плане производства. Целевая функция: Ограничения:  Решение задачи в MS Excel В качестве переменных х1 и х2 будем использовать ячейки E2 и E3 соответственно. Для значения целевой функции будем использовать ячейку E9: 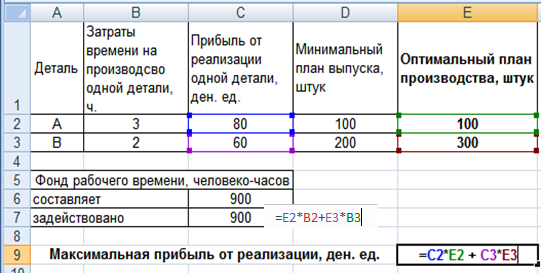 Рис. 2 Далее выбираем пункт меню Сервис/Поиск решения: 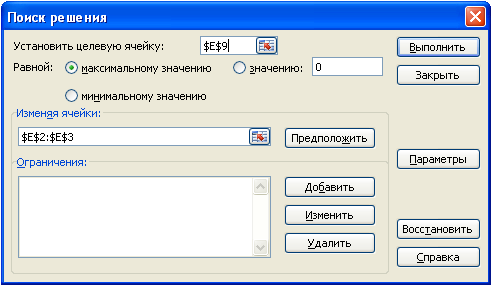 Рис. 3 Перед нами открывается диалоговое окно Поиск решения. В нём указываем, что нам необходимо установить ячейку $E$9 максимальному значению, изменяя ячейки $E$2:$E$3. Далее нажимаем кнопку Добавить для добавления ограничений. И добавляем следующие ограничения: 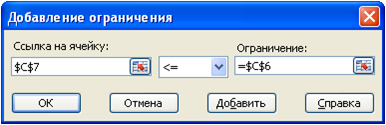 Рис. 4 Ограничения по фонду рабочего времени  Рис. 5 Ограничения по минимальному плану производства  Рис. 6 Количество изделий должно быть целым числом После ввода каждого ограничения нажимаем кнопку Добавить. После ввода последнего ограничения нажимаем кнопку OK. И диалоговое окно Поиск решения принимает следующий вид: 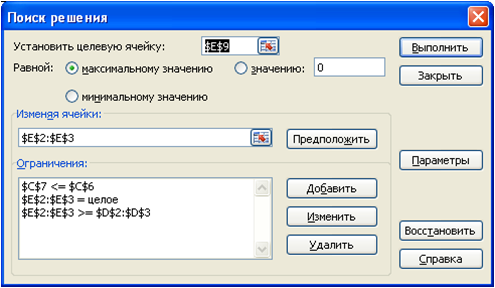 Рис. 7 Нажимаем кнопку Выполнить. И перед нами открывается диалоговое окно Результаты поиска решения:  Рис. 8 Выбираем создание отчёта по результатам. Отчеты по устойчивости и пределам не создаются при использовании целочисленных ограничений на переменные. После нажатия кнопки OK в рабочей книге появляется новый лист с названием Отчет по результатам 1 содержащий отчёт по результатам, и получаем следующие результаты:  Рис. 9 Пример №2 Кондитерской фабрике в конце месяца дано задание выпустить свою продукцию в виде подарочных наборов из конфет разных сортов. Состав каждого набора задан, количество конфет ограничено (см.таблицу). Определите, сколько и какого типа наборов нужно выпустить, чтобы получить максимальную прибыль.
Математическая модель задачи Обозначим за x1 количество наборов «Праздник», x2 - количество наборов «Сюрприз», x3 – количество наборов «Привет». Целевая функция: Ограничения: 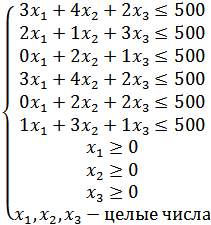 Решение задачи в MS Excel В качестве переменных х1, х2, x3 будем использовать ячейки С10, D10 и E10 соответственно. Для значения целевой функции будем использовать ячейку F11:  Рис.10 В диалоговом окне Поиск решения указываем, что нам необходимо установить в ячейку $F$11 максимальному значению, изменяя ячейки $C$10:$D10. B добавляем следующие ограничения:  Рис.11 Получаем следующие результаты:  Рис.12 Пример №3 Фирма, обслуживающая туристов прибывающих на отдых, должна разместить их в 4 отелях: “Морской”, “Солнечный”, “Слава” и “Уютный”, в которых забронировано соответственно 5, 15, 15 и 10 мест. Пятнадцать туристов прибывают по железной дороге, двадцать пять прилетают очередным рейсом в аэропорт, а пять человек прибудут на теплоходе на морской вокзал. Транспортные расходы при перевозке из пунктов прибытия в отели приведены в таблице 1.
Таблица 1 В условиях жесткой конкуренции фирма должна минимизировать свои расходы, значительную часть которых составляет именно транспортные расходы. Требуется определить такой план перевозки туристов из пункта прибытия в отели, при котором суммарные транспортные расходы будут минимальны и все туристы будут размещены в отелях. Математическая модель задачи 1) Переменные задачи. Обозначим количество туристов, которые будут перевозиться из пункта i в отель j как Xij (i=1,2,3; j=1,2,3,4). Это переменные задачи, значения которых должны быть определены в процессе решения. Например, X23 – это число туристов, которое должно быть перевезено из аэропорта (пункт 2) в отель “Слава” (пункт 3). В задаче содержится 3*4=12 переменных. 2) Ограничения на переменные задачи. Очевидно, что все переменные задачи не отрицательные и целые числа, т.е. Xij – целые числа, (2) где i=1, 2, 3; j=1, 2, 3, 4. Кроме этого, должны быть удовлетворяться следующие условия. Число туристов, вывозимых с железнодорожного вокзала (пункт 1) равно 15, поэтому: X11 + X12 + X13 + X14 = 15 (3) Аналогично для аэропорта (пункт 2): X21 + X22 + X23 + X24 = 25 (4) И для морского вокзала (пункт 3): X31 + X32 + X33 + X34 = 5 (5) По условию задачи в отеле “Морской” (пункт 1) забронировано 5 мест, поэтому: X11 + X21 + X31 = 5 (6) Аналогично, для отеля “Солнечный” (пункт 2): X12 + X22 + X32 = 15 (7) Для отеля “Слава” (пункт 3): X13 + X23 + X33 =15 (8) Для отеля “Уютный” (пункт 4): X14 + X24 + X34 =10 (9) Обычно транспортная задача представляется в виде таблицы, где в ячейках помещаются переменные задачи (Xij), а в правом верхнем углу ячейки стоят стоимости перевозки из пункта i в пункт j (Cij). В крайнем правом столбце и нижней строке таблицы записываются числа определяющие ограничения задачи (в данном примере – это число туристов в исходных пунктах и число мест в пунктах назначения – отелях). Для примера 2 таблица имеет вид:
Таблица 2 3) Целевая функция. Транспортные расходы на перевозку туристов в отели вычисляются по формуле: Z = CijXij = 10X11 + 0X12 + 20X13 + ... +18X34 (10) Окончательно транспортная задача имеет вид (таблица 2). Нужно найти такие значения переменных Xij (i=1,2,3; j=1,2,3,4) при которых целевая функция, определяемая формулой (10), будет иметь минимальное значение и будут выполнены ограничения (1) - (9) Как и в рассмотренной выше задаче оптимального выпуска продукции (пример 1) транспортная задача является задачей линейного программирования. Решение транспортной задачи в Excel 1) Ввод данных. Вводим данные таблицы 1 и 2 в ячейки Excel (рис.9). В ячейках B3 : E5 введены стоимости перевозок (табл. 1). В ячейках F3 : F5 находится число прибывающих туристов. А в ячейках B6 : E6 находится число мест в отелях. Ячейки B8 : E10 – рабочие (изменяемые) ячейки, в которых будут вычисляться значения переменных задачи Xij. В ячейках F8 : F10 нужно записать формулы для вычисления левых частей ограничений (3)-(5): в F8 должна быть сумма ячеек B8 : E8; в F9 должна быть сумма ячеек B9 : E9; в F10 должна быть сумма ячеек B10 : E10. Формулы для вычисления левых частей ограничений (6)-(9) введем в ячейки B11 : E11: в B11 должна быть сумма ячеек B8 : B10; в C11 должна быть сумма ячеек C8 : C10; в D11 должна быть сумма ячеек D8 : D10; в E11 должна быть сумма ячеек E8 : E10; Целевую функцию поместим в ячейку G3: G3: СУММПРОИЗВ (B3 : E5; B8 : E10). Таблица исходных данных имеет вид (Рис.13):  Рис. 13 2) Заполнение окна процедуры «Поиск решения». целевая функция : G3; значение целевой функции : min; изменяемые ячейки : B8 : E10; ограничения задачи : F8 : F10 = F3 : F5 (формулы (3)-(5)) B11 : E11 = B6 : E6 (формулы (6)-(9)) B8 : E10 >=0 (1) и B8 : E10 – целые числа (2) В окне «Параметры» установить «Линейная модель». Результаты заполнения окна показаны на рис.14:  Рис.14 Рис.143) Выполнив процедуру «Поиск решения» получим следующие результаты: 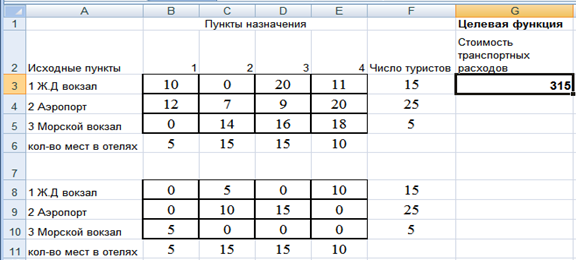 Рис. 15 Таким образом, с железнодорожного вокзала (исходный пункт 1) следует 10 туристов отвезти в отель «Уютный» (пункт 4) и 5 туристов в отель «Солнечный» (пункт назначения 2); из аэропорта (исходный пункт 2) 10 туристов отвезти в отель «Солнечный» (пункт назначения 2) и 15 туристов в отель «Слава» (пункт назначения 3); туристов прибывающих на морской вокзал (исходный пункт 3) нужно отправить в отель «Морской» (пункт назначения 1). Все эти результаты видны в конечной таблице (рис.12) При этом суммарная стоимость транспортных расходов составит 315 рублей (ячейка G3). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
