Лабораторная работа 1 Статистическое описание результатов наблюдений. Числовые оценки выборочного распределения. Интервальные оценки для математического ожидания и дисперсии. Проверка гипотезы о виде распределения
 Скачать 222.41 Kb. Скачать 222.41 Kb.
|
|
Теория вероятностей и математическая статистика Лабораторная работа № 1 « Статистическое описание результатов наблюдений. Числовые оценки выборочного распределения. Интервальные оценки для математического ожидания и дисперсии. Проверка гипотезы о виде распределения» 1. Получите выборку из 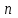 чисел чисел2. Постройте вариационный ряд (упорядочите элементы выборки по величине). При этом можно использовать соответствующую команду на панели инструментов Excel. 3 .Представьте выборку в виде группированного статистического ряда (с.178- 181) определите размах выборки 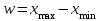 определите число интервалов группировки одним из способов: а) Способ 1: выбираете число интервалов 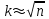 , а затем находите шаг (ширину интервала группировки) , а затем находите шаг (ширину интервала группировки) 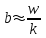 , б) Способ 2: выбираете шаг (ширину интервала группировки) по формуле , б) Способ 2: выбираете шаг (ширину интервала группировки) по формуле 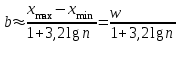 . .Определите границы интервалов группировки 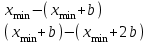 , и так далее до тех пор, пока наибольший элемент выборки не попадет в последний интервал ( наилучшая ситуация, если он точно совпадает с верхней границей последнего интервала) , и так далее до тех пор, пока наибольший элемент выборки не попадет в последний интервал ( наилучшая ситуация, если он точно совпадает с верхней границей последнего интервала)Найдите середину каждого интервала 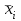 Определите частоты 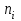 - число элементов выборки, содержащихся в каждом - число элементов выборки, содержащихся в каждом 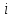 -м интервале. При этом элемент, совпадающий с верхней границей интервала, условимся относить к следующему интервалу. -м интервале. При этом элемент, совпадающий с верхней границей интервала, условимся относить к следующему интервалу.Найдите накопленные частоты 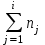 . При этом сумма частот по всем интервалам должна совпадать с объемом выборки . При этом сумма частот по всем интервалам должна совпадать с объемом выборки 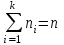 . Если сумма частот по всем интервалам не совпадает с объем выборки, то следует проверить, правильно ли найдены частоты. . Если сумма частот по всем интервалам не совпадает с объем выборки, то следует проверить, правильно ли найдены частоты.Найдите относительные частоты 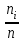 , которые служат оценкой вероятности попадания элемента выборки в данный интервал , которые служат оценкой вероятности попадания элемента выборки в данный интервалНайдите относительные накопленные частоты 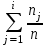 . Значения накопленных частот служат оценкой функции распределения и определяют эмпирическую ( выборочную) функцию распределения . Значения накопленных частот служат оценкой функции распределения и определяют эмпирическую ( выборочную) функцию распределения 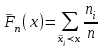 Представляем выборку графически строим полигон частот- ломаную с вершинами в точках ( 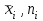 ) (вставляем график) ) (вставляем график)строим полигон относительных частот- ломаную с вершинами в точках ( 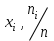 ) )строим гистограмму - кусочно-постоянную функцию, которая на каждом интервале группировки принимает значение 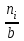 . Площадь ступенчатой фигуры под графиком гистограммы равна объему выборки . Площадь ступенчатой фигуры под графиком гистограммы равна объему выборки 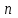 . .Полигон относительных частот является статистическим аналогом функции плотности вероятности. Гистограмма и полигон частот отличаются от указанной характеристики растяжением в 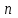 раз. Поэтому все данные функции также являются характеристиками закона распределения генеральной совокупности раз. Поэтому все данные функции также являются характеристиками закона распределения генеральной совокупности 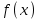 . .5. Определяем основные числовые характеристики выборочного распределения Оценкой математического ожидания является выборочное среднее 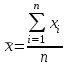 , ,если каждый элемент выборки встречается один раз. Если элемент выборки 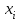 имеет частоту имеет частоту 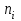 , то выборочное среднеенаходят по формуле , то выборочное среднеенаходят по формуле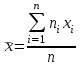 . .В том случае, если выборка группированная, то вместо элемента выборки в этой формуле берут середину интервала, а за частоту берут число элементов, попадающих в данный интервал. Выборочная дисперсия 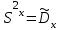 служит оценкой дисперсии распределения генеральной совокупности и определяется по следующим формулам служит оценкой дисперсии распределения генеральной совокупности и определяется по следующим формуламЕсли каждый элемент выборки встречается только один раз 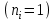 и объем выборки достаточно велик ( и объем выборки достаточно велик ( 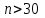 ), то следует использовать формулу ), то следует использовать формулу 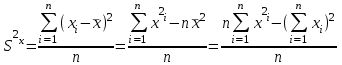 . .Для выборок малого объема несмещенную (исправлннную) дисперсию следует вычислять по формуле 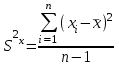 Если частота каждого элемента 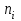 , то для выборок большого объема следует использовать формулу , то для выборок большого объема следует использовать формулу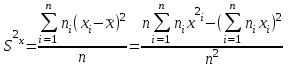 . .Для группированных выборок в этой формуле нужно использовать середину интервала и число элементов, попадающих в этот интервал. (Таблица пример выдачи данных) Пример выдачи данных: Интервальные оценки ( доверительные интервалы) параметров распределения Доверительным интервалом называют интервал, содержащий истинное значение параметра с заданной вероятностью 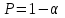 , которую называют доверительной вероятностью. , которую называют доверительной вероятностью.В тех случаях, когда дисперсия генеральной совокупности неизвестна, а получена ее оценка по указанным выше формулам, доверительный интервал для математического ожидания имеет вид: 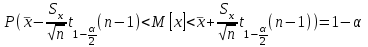 Здесь 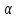 - уровень значимости. Ширина доверительного интервала характеризует точность оценивания или стандартную ошибку - уровень значимости. Ширина доверительного интервала характеризует точность оценивания или стандартную ошибку 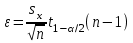 и зависит от объема выборки и доверительной вероятности (уровня значимости). С увеличением объема выборки ширина доверительного интервала уменьшается (точность оценивания возрастает), а по мере приближения доверительной вероятности к единице (приближении уровня значимости к нулю) ширина доверительного интервала увеличивается ( точность оценивания падает). и зависит от объема выборки и доверительной вероятности (уровня значимости). С увеличением объема выборки ширина доверительного интервала уменьшается (точность оценивания возрастает), а по мере приближения доверительной вероятности к единице (приближении уровня значимости к нулю) ширина доверительного интервала увеличивается ( точность оценивания падает).Здесь 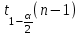 квантиль распределения Стьюдента. или в Excel на панели инструментов находите статистические функции и распределение Стьюдента. квантиль распределения Стьюдента. или в Excel на панели инструментов находите статистические функции и распределение Стьюдента.Доверительный интервал для дисперсии в том случае, если математическое ожидание неизвестно, а оценки получены по выборке, находим согласно соотношению 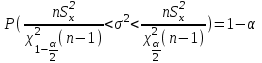 Результат РезультатЗдесь 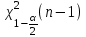 , , 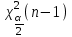 квантили распределения или в Excel. квантили распределения или в Excel. 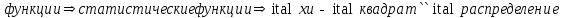 . .Проверка гипотезы о виде распределения генеральной совокупности На следующем этапе работы по виду полигона частот (гистограммы ) и полученным значениям числовых характеристик выдвигаем гипотезу о виде распределения генеральной совокупности и проверяем соответствие данной гипотезы эмпирическим данным. После того, как выдвинули гипотезу, находим теоретические частоты, соответствующие предполагаемому распределению: 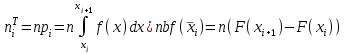 По виду гистограммы и полигона частот выдвигаем гипотезу : Выборка получена из нормально распределенной генеральной совокупности. Этот закон имеет два параметра, оценки которых находим по выборке: 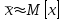 - выборочное среднее приравниваем к математическому ожиданию, - выборочное среднее приравниваем к математическому ожиданию,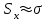 - выборочное среднеквадратичное отклонение (стандарт) приравниваем к его теоретическому значению. Функция плотности вероятности для нормированной переменной - выборочное среднеквадратичное отклонение (стандарт) приравниваем к его теоретическому значению. Функция плотности вероятности для нормированной переменной 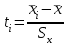 приводят по таблице на стр.408 приводят по таблице на стр.408 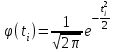 . Теоретическую частоту находим по формуле . Теоретическую частоту находим по формуле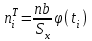 (Ещё формула без использования Sx, а ФИ берём в эксель (Ещё формула без использования Sx, а ФИ берём в эксельПолученные теоретические частоты наносим на полигон частот. Если согласие между эмпирическими и предполагаемыми теоретическими частотами визуально достаточно хорошее, то проводим проверку выдвинутой гипотезы по критерию 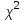 . При этом выборочное значение статистики критерия находят по формуле . При этом выборочное значение статистики критерия находят по формуле 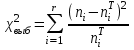 . Здесь . Здесь 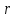 - число интервалов с учетом того, что - число интервалов с учетом того, что 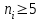 . Если это условие не выполняется, то объединяем соседние интервалы. Теоретическое значение статистики критерия находим по таблице на : . Если это условие не выполняется, то объединяем соседние интервалы. Теоретическое значение статистики критерия находим по таблице на :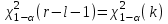 .К=5 , Альфа=0,1 Хи^2=9,… , Хи^2 выбороч=10,… В этом выражении .К=5 , Альфа=0,1 Хи^2=9,… , Хи^2 выбороч=10,… В этом выражении 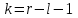  – число степеней свободы. Здесь – число степеней свободы. Здесь 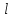 - это число параметров распределения, оцениваемых по выборке. Так для показательного закона - это число параметров распределения, оцениваемых по выборке. Так для показательного закона 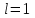 , для нормального закона и гамма-распределения , для нормального закона и гамма-распределения 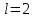 . К=5 , Альфа=0,1 Хи^2=9,… , Хи^2 выбороч=10,… . К=5 , Альфа=0,1 Хи^2=9,… , Хи^2 выбороч=10,…Если выполняется условие 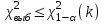 , то выдвинутая гипотеза не противоречит опытным данным на заданном уровне значимости , то выдвинутая гипотеза не противоречит опытным данным на заданном уровне значимости 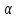 и не может быть отвергнута. и не может быть отвергнута.  ЛАБОРАТОРНАЯ РАБОТА № 2. ВЫБОРОЧНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ Коэффициент корреляции двух случайных величин определяет степень линейной корреляционной зависимости между ними 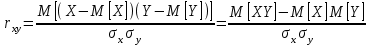 . .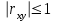 . Если . Если 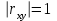 , то случайные величины связаны точной линейной зависимосью. , то случайные величины связаны точной линейной зависимосью. Выборочный коэффициент корреляции служит оценкой коэффициента корреляции и определяется выражением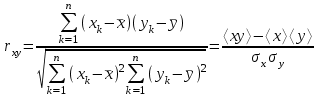 , где , где 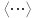 означает усреднение. означает усреднение.Можно непосредственно вычислять коэффициент по этой формуле, но удобнее выполнять действия по следующему алгоритму (стр. 196-198 или учебное пособие [2] ) . Полученное при помощи средств EXCEL значение коэффициента корреляции данных массивов равно 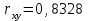 (СВОЁ). Выбираем (СВОЁ). Выбираем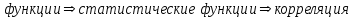 на панели инструментов. на панели инструментов.ШАГ 5. Проверяем гипотезу о статистической значимости выборочного коэффициента корреляции (стр. 265-266) Выдвигаем основную гипотезу 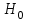 : :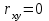 и соответствующую альтернативную гипотезу и соответствующую альтернативную гипотезу 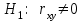 . На заданном уровне значимости . На заданном уровне значимости 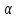 находим теоретическое значение статистики критерия согласно выражению находим теоретическое значение статистики критерия согласно выражению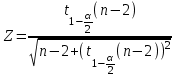 . .Выбрав уровень значимости 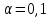 , находим по таблице (стр. 414) квантиль распределения Стьюдента , находим по таблице (стр. 414) квантиль распределения Стьюдента 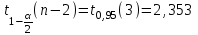 и вычисляем значение статистики и вычисляем значение статистики 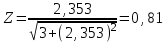 . (Своё) . (Своё)Основная гипотеза принимается, если выполняется соотношение 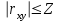 и отвергается в случае и отвергается в случае 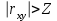 . .В рассматриваемом случае 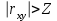 . Поэтому основная гипотеза отклоняется и принимается гипотеза . Поэтому основная гипотеза отклоняется и принимается гипотеза 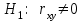 . Таким образом, коэффициент корреляции на выбранном уровне значимости отличен от нуля. Это свидетельствует о наличии корреляционной зависимости между случайными величинами. Значение коэффициента корреляции близко к единице , что говорит о близости зависимости между случайными величинами к линейной зависимости. (Свои числа) . Таким образом, коэффициент корреляции на выбранном уровне значимости отличен от нуля. Это свидетельствует о наличии корреляционной зависимости между случайными величинами. Значение коэффициента корреляции близко к единице , что говорит о близости зависимости между случайными величинами к линейной зависимости. (Свои числа)2. НАХОЖДЕНИЕ ПАРАМЕТРОВ УРАВНЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ ( стр. 291- 298 ) Пусть коэффициент корреляции между двумя случайными величинами значимо отличается от нуля и близок к единице. Предполагаем ( выдвигаем гипотезу ) , что эти случайные величины связаны « в среднем» линейной зависимостью : 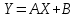 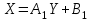 РЕГРЕССИЯ – оптимальная зависимость, то есть модель, обеспечивающая аппроксимацию эмпирических данных с наибольшей точностью. Справедливо соотношение 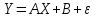 Коэффициенты 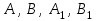 являются параметрами линейной регрессионной модели. Величина являются параметрами линейной регрессионной модели. Величина 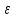 - случайная ошибка наблюдений, причем математическое ожидание - случайная ошибка наблюдений, причем математическое ожидание 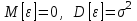 Для нахождения оценок параметров модели используем метод наименьших квадратов. Согласно этому методу в качестве оценок параметров выбирают такие, которые обеспечивают минимум суммы квадратов отклонений наблюдаемых значений случайных величин от их математических ожиданий. Другими словами параметры должны быть такими, чтобы сумма 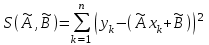 принимала наименьшее значение. Записываем необходимые условия существования экстремума для функции двух переменных принимала наименьшее значение. Записываем необходимые условия существования экстремума для функции двух переменных 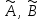 , приравнивая к нулю частные производные , приравнивая к нулю частные производные 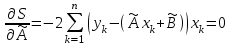 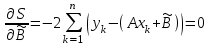 В результате для нахождения оценок получаем систему уравнений: 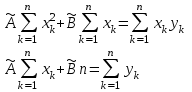 Решение системы имеет вид : 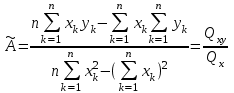 , , 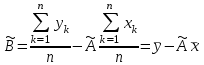 . .Аналогично находим оценки 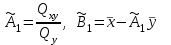 . При этом . При этом 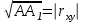 . .СВОЙИ ГРАФИК | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
имеем оценки СВОИ ОЦЕНКИ
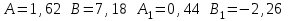
И уравнения регрессии имеют вид
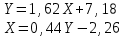 (ИКС убрать)
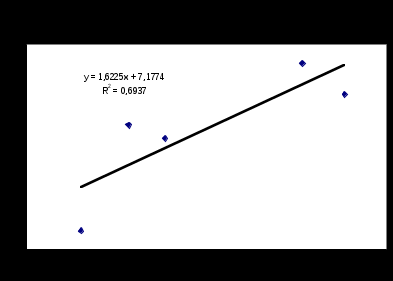
(ИКС убрать)Достаточно легко написать программу для получения оценок по методу наименьших квадратов как для линейной , так и для других зависимостей. Но существует много готовых программных средств, решающих эту задачу. Так средства EXCEL позволяют непосредственно получить уравнение линейной регрессии по рядам данных:
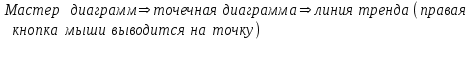
Регрессионная модель называется адекватной, если предсказанные по ней значения переменной
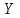 согласуются с результатами наблюдений. Оценка адекватности может быть проведена следующим образом.
согласуются с результатами наблюдений. Оценка адекватности может быть проведена следующим образом.Непосредственный анализ остатков, то есть разностей между наблюдаемыми значениями
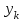 и вычисленными согласно уравнению регрессии
и вычисленными согласно уравнению регрессии 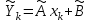 :
: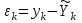 .
.Если модель адекватна, то остатки, которые являются реализациями случайных ошибок наблюдений, должны быть нормально распределенными случайными величинами с нулевым средним и одинаковыми дисперсиями
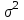 . Другими словами для случайной величины - остатков – необходимо выполнить лабораторную работу № 1(найти среднее, дисперсию, среднеквадратичное отклонение) и доказать, что на заданном уровне значимости
. Другими словами для случайной величины - остатков – необходимо выполнить лабораторную работу № 1(найти среднее, дисперсию, среднеквадратичное отклонение) и доказать, что на заданном уровне значимости 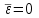 (нулевое значение
(нулевое значение 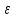 попадает в доверительный интервал для математического ожидания).
попадает в доверительный интервал для математического ожидания).Пример построения прямой регрессии в Excel.
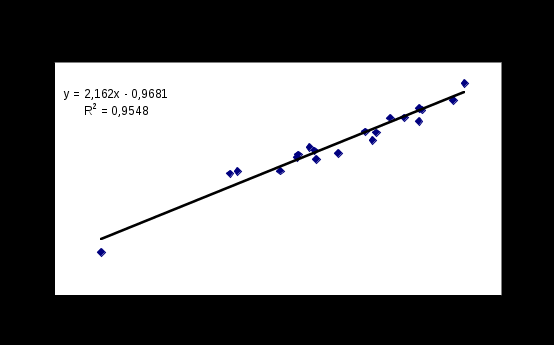
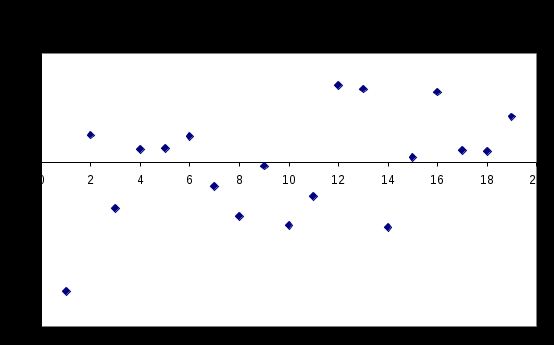
Данные описательной статистики для случайной величины “остатки”
СВОИ ВСТАВЛЯЕМ
| Среднее | 6,66134E-16 |
| Стандартная ошибка | 0,108822029 |
| Медиана | 0,109108445 |
| Мода | |
| Стандартное отклонение | 0,486666907 |
| Дисперсия выборки | 0,236844679 |
| Эксцесс | 0,294111648 |
| Асимметричность | -0,602186657 |
| Интервал | 1,892506228 |
| Минимум | -1,181791019 |
| Максимум | 0,710715209 |
| Сумма | 1,33227E-14 |
| Счет | 20 |
| Уровень надежности(95,0%) | 0,227767194 |
Из приведенных зависимостей и расчетов видно, что предложенная регрессионная модель адекватна: остатки распределены около нулевого среднего. Значение стандартной ошибки
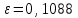 задает доверительный интервал для
задает доверительный интервал для 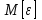 , содержащий значение
, содержащий значение 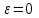 .
.Статистическую значимость регрессионной модели можно проверить по коэффициенту регрессиии
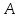 .
.Линейная регрессионная модель называется незначимой, если параметр
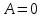 . Проверку основной гипотезы
. Проверку основной гипотезы 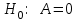 против альтернативной гипотезы
против альтернативной гипотезы 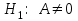 можно провести двумя способами.
можно провести двумя способами.СПОСОБ 2 . Находим границы доверительного интервала для параметра
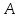 :
: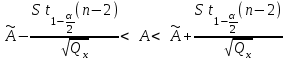
Если для данного уровня значимости доверительный интервал содержит значение
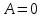 , то принимается основная гипотеза и регрессия считается статистически незначимой. В том случае, когда доверительный интервал не содержит нулевое значение параметра, основная гипотеза отклоняется и регрессионная модель считается статистически значимой
, то принимается основная гипотеза и регрессия считается статистически незначимой. В том случае, когда доверительный интервал не содержит нулевое значение параметра, основная гипотеза отклоняется и регрессионная модель считается статистически значимойНапример :
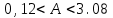 или
или 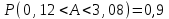 . СОВИ ЧИСЛА
. СОВИ ЧИСЛАТаким образом, на заданном уровне значимости нулевое значение параметра не попадает в доверительный интервал и регрессия признается статистически значимой
Полезной и важной характеристикой линейной регрессии является коэффициент детерминации
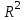 , который вычисляют по формуле
, который вычисляют по формуле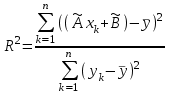 .
.Этот коэффициент показывает долю разброса результатов наблюдений около средего значения случайной величины
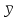 , которую можно объяснить построенной регрессионной моделью , и может быть использован для характеристики не только линейной регрессии, но и для нелинейной. Как видно из определения коэффициента, чем меньше остаточная сумма квадратов
, которую можно объяснить построенной регрессионной моделью , и может быть использован для характеристики не только линейной регрессии, но и для нелинейной. Как видно из определения коэффициента, чем меньше остаточная сумма квадратов 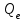 , тем ближе значение коэффициента к единице и тем точнее выбранная модель регрессии описывает результаты наблюдений. Значение корня
, тем ближе значение коэффициента к единице и тем точнее выбранная модель регрессии описывает результаты наблюдений. Значение корня 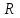 является оценкой коэффициента корреляции между результатами наблюдений и их значениями, вычисленными согласно принятой регрессионной модели. В случае линейной регресссии справедливо
является оценкой коэффициента корреляции между результатами наблюдений и их значениями, вычисленными согласно принятой регрессионной модели. В случае линейной регресссии справедливо 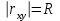 . Отметим, что именно значение коэффициента детерминации указывается в EXCEL в качестве характеристики качества аппроксимации.
. Отметим, что именно значение коэффициента детерминации указывается в EXCEL в качестве характеристики качества аппроксимации. Ниже приведена выдача из Excel:
 , для подробного анализа которой следует обратиться к книге [3]. Отметим только, что красным цветом выделен 95% доверительный интервал для коэффициента регрессии
, для подробного анализа которой следует обратиться к книге [3]. Отметим только, что красным цветом выделен 95% доверительный интервал для коэффициента регрессии 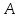 :
: 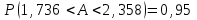 . СВОЁ ВСТАВИТЬ
. СВОЁ ВСТАВИТЬ| | ВЫВОД ИТОГОВ | | | | | | | |||||||||
| | | | | | | | | | ||||||||
| | Регрессионная статистика | | | | | | | |||||||||
| | Множественный R | 0,956037 | | | | | | | ||||||||
| | R-квадрат | 0,914006 | | | | | | | ||||||||
| | Нормированный R-квадрат | 0,909229 | | | | | | | ||||||||
| | Стандартная ошибка | 0,500003 | | | | | | | ||||||||
| | Наблюдения | 20 | | | | | | | ||||||||
| | | | | | | | | | ||||||||
| | Дисперсионный анализ | | | | | | ||||||||||
| | | df | SS | MS | F | Значимость F | | | ||||||||
| | Регрессия | 1 | 47,83 | 47,83 | 191,3179 | 4,96562E-11 | | | ||||||||
| | Остаток | 18 | 4,500049 | 0,250003 | | | | | ||||||||
| | Итого | 19 | 52,33004 | | | | | | ||||||||
| | | | | | | | | | ||||||||
| | | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | | ||||||||
| | Y-пересечение | -0,43605 | 0,718975 | -0,60648 | 0,5517664 | -1,946557679 | 1,074464255 | | ||||||||
| | Переменная X 1 | 2,047796 | 0,14805 | 13,83177 | 4,966E-11 | 1,736753836 | 2,358837984 | | ||||||||
| | | | | | | | | | ||||||||
| | | | | | | | | | ||||||||