Лабораторная работа 1. Лабораторная работа 1. Задание 1
 Скачать 190.99 Kb. Скачать 190.99 Kb.
|
|
Лабораторная работа №1. Задание 1. Четыре человека взялись выполнять работу маляра, слесаря, кузнеца и штукатура – каждый будет делать что-то одно. Выяснилось, что Антон не будет маляром и не будет слесарем, Алексей не будет кузнецом и не будет маляром, Евгений не будет слесарем и не будет маляром, Дмитрий не будет кузнецом и не будет слесарем. Известно также, что если Антон не будет кузнецом, то Дмитрий не будет маляром. Кто и какую работу будет выполнять? Люди: Антон, Алексей, Евгений, Дмитрий Антон: не маляр, не слесарь Алексей: не кузнец, не маляр Дмитрий: не кузнец, не слесарь
Исходя из начальных условий, так как ни Антон, ни Алексей, ни Евгений не будут маляром, то маляром будет Дмитрий. Известно также, что если Антон не будет кузнецом, то Дмитрий не будет маляром. Так как маляром будет Дмитрий, то Антон должен быть кузнецом. Так как ни Антон, ни Дмитрий, ни Евгений не будут слесарем, то слесарем будет Алексей. В этом случае, так как каждый будет делать что-то одно, Евгений может быть только штукатуром.
Таким образом, в итоге получается, что кузнец - Антон, слесарь - Алексей, штукатур - Евгений, маляр - Дмитрий. Лабораторная работа №2 Задание 1.  Изделия А, В и С могут производиться в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида. Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной. 18х1 + 15х2 + 12х3 ≤ 360, 6х1 + 4х2 + 8х3 ≤ 192 5х1 + 3х2 + 3х3 ≤ 180 F = 9х1 + 10х2 + 16х3 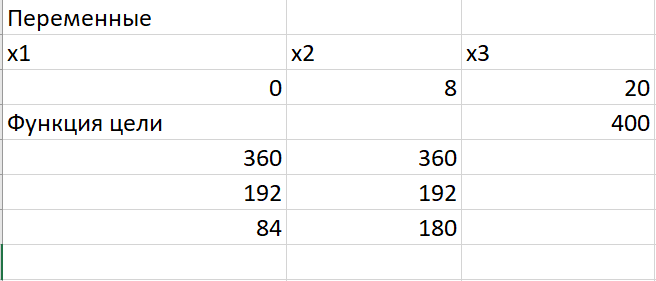 Задание 2. На трех железнодорожных станциях скопилось 120, 110 и 130 незагруженных вагонов. Эти вагоны необходимо перегнать на железнодорожные станции В1, В2, ВЗ, В4 и В5. На каждой из этих станций потребность в вагонах соответственно равна 80, 60, 70, 100 и 50. Тарифы перевозок задаются матрицей  Составить такой план перегонок вагонов, при котором общая стоимость была бы минимальной.  Лабораторная работа №3 Задание 1. соответствует максимальное значение ОДО.                            * * Благоприятное состояние Неблагоприятное состояние Благоприятное состояние Неблагоприятное состояние а1 а2 Маленькая мастерская Большая мастерская 30 000 - 30 000 60 000 - 65 000 1 2                               10 000 * * Благоприятное состояние Неблагоприятное состояние Благоприятное состояние Неблагоприятное состояние а1 а2 30 000 - 30 000 60 000 - 65 000 1 2 // // Маленькая мастерская Большая мастерская Без дополнительного обследования наиболее целесообразно выбрать стратегию а2, т.е. открыть большую мастерскую, а ветвь (стратегию) а1 дерева решений можно отбросить. ОДО наилучшего решения равна 10 000 руб. Задание 2.                                                                          Прогноз благоприятный (0,5) Проводить обследование 201 000 Прогноз неблагоприятный (0,5) -13 000 * 201 000 75 800 * * Благоприятное (0,8) Неблагоприятное (0,2) Благоприятное(0,8) а1 а2 Маленькая мастерская Большая мастерская 30 000 - 30 000 60 000 Неблагоприятное (0,2) - 65 000 3 4 // 19 700 -28 500 16 400 19 700 * * Благоприятное (0,3) Неблагоприятное (0,7) Благоприятное (0,3) а1 а2 маленькая мастерская большая мастерская 30 000 - 30 000 60 000 - 65 000 5 6 // Еcли фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно открывать большую мастерскую (ожидаемая максимальная прибыль 35 000 рублей), если прогноз неблагоприятный – не открывать мастерскую, так как в этом случае любая мастерская принесет убыток |
