Лабораторная работы (1). Лабораторная работа 1 Задание 1
 Скачать 5.5 Mb.
|
|
Лабораторная работа 1  Задание 1 Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и запишите искомое значение. Определите число верных знаков. a=0.02456±0.00005; b=0.20078±0.00005; c=0.008±0.00013   - точное значение - приближенное значениеΔx-абсолютная погрешность  - относительная погрешность Порядок выполняемых операций: Находим абсолютную и относительную погрешности (a+b); (a+b)*c; (a-b); (a+b)*c/(a-b) 1+c Ln(1+c) Ln^2(1+c); Ln^2(1+c)*(a+b)*c/(a-b); Воспользуемся универсальными оценками: df/da=18.49331 df/db=0.0199724 df/dc= 1.83595962 Предельная абсолютная погрешность:   F=  = 0.008814431Определение числа верных знаков:  ;  ;  6: 5*  < 2.9308* 8: 5*  < 2.9308* 9: 5*  < 2.9308* 9: 5*  < 2.9308* 4: 5*  < 2.9308* 2: 5* > 2.9308* 3: 5*  > 2.9308* 3: 5*  > 2.9308* Следовательно 2, 3, 3 верные цифры. Ответ: m=3, F=-3.3249986* .Задание 2 Выясните погрешность задания исходных данных, необходимую для получения результата с m верными значащими цифрами m=4, a=0.02456; b=0.07823; c=0.8348. Полагаем верными 5 цифр, тогда Относительная погрешность  Абсолютная погрешность  * *  ;a*  0.02456* = 0.45419569b*  0.01823* = 0.0001836209 0.348*1.83595962 = 0.63891395a*  b* + Допустимая погрешность данных 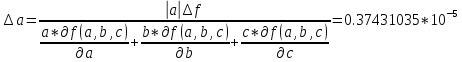 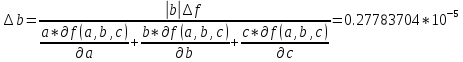 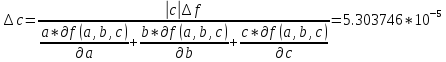   Таблица значений:
Соответственно полученные пределы: an=0,752017222 bn=7,37811988    Лабораторная работа 4   Согласно основной теоремы алгебры, количество корней многочлена равно его максимальной степени, значит у этого выражение 4 корня. Если на концах отрезка функция принимает различные по знаку значения, значит между ними есть как минимум один корень (справедливо только для непрерывных на отрезке функций) Этому условию удовлетворяет отрезок от 0 до 2, возьмём его Метод Дихотомии: Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε. Итак, имеем f(a)f(b)<0. Метод дихотомии заключается в следующем. Определяем половину отрезка c=1/2(a+b) и вычисляем f(c). Проверяем следующие условия: 1. Если |f(c)| < ε, то c – корень. Здесь ε - заданная точность. 2. Если f(c)f(a)<0, то корень лежит в интервале [a,c]. 3. Если f(c)f(b)<0, то корень лежит на отрезке[c,b]. Продолжая процесс половинного деления в выбранных подынтервалов, можно дойти до сколь угодно малого отрезка, содержащего корень ξ. Так как за каждую итерацию интервал, где расположен корень уменьшается в два раза, то через n итераций интервал будет равен: bn-an=1/2n(b-a) В качестве корня ξ. возьмем 1/2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие: (bn – an)/2 < ε то процесс поиска заканчивается и ξ = 1/2(an+bn). Число шагов, необходимых для достижения заданной точности определяется неравенством:  F(0)=-3; F(2)=3 Поскольку F(0)*F(2)<0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [0;2]. Находим середину отрезка: c = (0 + 2)/2 = 1 F(x) = -2 F(c) = -3 Поскольку F(c)•F(b) < 0, то a=1 Находим середину отрезка: c = (1 + 2)/2 = 1.5 F(x) = -1.313 F(c) = -2 Поскольку F(c)•F(b) < 0, то a=1.5 Находим середину отрезка: c = (1.5 + 2)/2 = 1.75 F(x) = 0.145 F(c) = -1.313 Поскольку F(c)•F(a) < 0, то b=1.75 Находим середину отрезка: c = (1.5 + 1.75)/2 = 1.625 F(x) = -0.724 F(c) = 0.145 Поскольку F(c)•F(b) < 0, то a=1.625 Нужная точность достигнута MatLab
Вывод: 1.625 Метод хорд: Рассмотрим более быстрый способ нахождения корня на интервале [a,b], в предположении, что f(a)f(b)<0. Уравнение хорды:  В точке x=x1, y=0, в результате получим первое приближение корня  Проверяем условия: 1. f(x1)f(b)<0, 2. f(x1)f(a)<0. Если выполняется условие (1), то в формуле точку a заменяем на x1, получим:  Продолжая этот процесс, получим для n-го приближения:  Пусть f(xi)f(a)<0. Записав уравнение хорды, мы на первом шаге итерационного процесса получим x1. Здесь выполняется f(x1)f(a)<0. Затем вводим b1=x1 (в формуле точку b заменяем на x1), получим:  Продолжая процесс, придем к формуле:  Останов процесса: |xn – xn-1|< ε, ξ = xn. Находим первую производную: dF/dx = 4•x3-3•x2-4•x+3 Находим вторую производную: d2F/dx2 = 2•(6•x2-3•x-2)
Вывод: 1.6930 Matlab: function MethodHord a=0 b=2 eps=1.*10^(-1) while ( (b-a)>eps) c=(a+b)./2; d=func(a).*func(c); if (d>0) a=c; else b=c; end end x=(a+b)./2; x end function f = func(x); f=x^4-x^3-2x^2+3x-3 end Вывод: 1.6930 Задание 2 График: 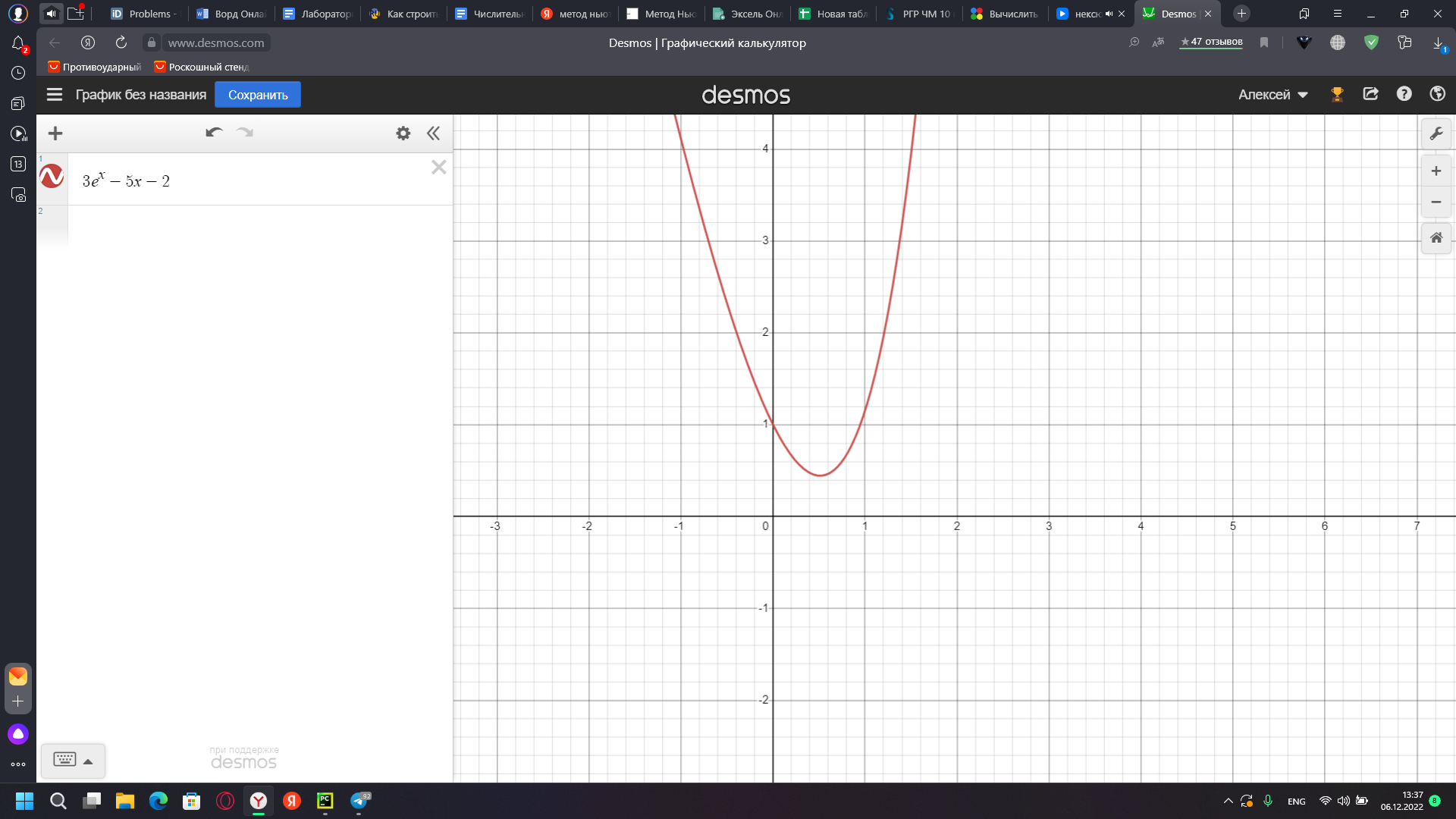 Проведем исследование решения уравнения: y=3e^x-5x-2 dy/dx=3e^x-5=0 x=ln(5/3) Так как слева производная отрицательна а справа положительна то эта точка является наименьшей точкой функции, значение функции в этой точке равно примерно 0.446. Значит функция не пересекает ось x, а значит не имеет корней. Задание 3 Пусть корень ξ уравнения f(x)=0 отделен на отрезке [a,b]. Предположим мы нашли (n-1)-ое приближение корня xn-1. Тогда n-ое приближение xn мы можем получить следующим образом. Положим: xn = xn-1 + hn-1 Раскладывая в ряд f(x=ξ) в точке xn-1, получим: f(xn) = f(xn-1+hn-1) = f(xn-1) + f’(xn-1)hn-1=0 Отсюда следует:  Подставим hn-1 в формулу, получим:  Геометрически метод Ньютона эквивалентен замене дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой. Находим первую производную:  Находим вторую производную:  = 3* / +9*x/ -  * - * / F(-1)=-0.841; F(0)=0.841 Поскольку F(-1)*F(0)<0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [-1;0]. Вычисляем значения функций в точке a = -1 f(-1) = -0.841 f''(-1) = не сущ. Критерий остановки итераций. |f(xk)| < εm1 или  где M2 = max|f "(x)|, m1 = min|f'(x)|. Поскольку f(a)•f''(a) < 0, то x0 = b = 0 Ответ: x = 0 - 0.8415 / (-0.9597) = 0.87680838450809; F(x) = 0.345 Matlab: x0 = [3; 1]; syms xs ys; %создаем символьные переменные, чтобы вычислить производную df1xs = diff('cos(xs-1) + ys - 0.5', xs); %производная 1 функции по x df1ys = diff('cos(xs-1) + ys - 0.5', ys); %производная 1 функции по y df2xs = diff('xs - cos(ys) - 3', xs); %производная 2 функции по x df2ys = diff('xs - cos(ys) - 3', ys); %производная 2 функции по y f0=[sin(x+y)-1,5xy=0; x^2+y^2=1]; %помещаем функции в вектор столбец df1x = double(subs(subs(df1xs, xs, x0(1)), ys, x0(2))); %определяем значение производных подставляя значение из начального приближения df1y = double(subs(subs(df1ys, xs, x0(1)), ys, x0(2))); df2x = double(subs(subs(df2xs, xs, x0(1)), ys, x0(2))); df2y = double(subs(subs(df2ys, xs, x0(1)), ys, x0(2))); w = [df1x df1y; df2x df2y]; %матрица Якоби det(w); % определитель, не должен быть равен 0 x = x0 - inv(w) * f0; %решение после первой итерации e = 0.01; %точность k = 1;; while or((abs(x(1) - x0(1)) > e), (abs(x(2) - x0(2)) > e)) %пока точность не будет достигнута x0(1) = x(1); x0(2) = x(2); f0=[sin(x+y)-1,5xy=0; x^2+y^2=1]; w = [(-sin(x0(1) - 1)) 1; 1 sin(x0(2))]; %матрица Якоби det(w); % определитель, не должен быть равен 0 x = x0 - inv(w) * f0; % новое решение k = k + 1; if ( k > 100) break; end; end; |