лабораторные работы. Лабораторные работы 5, 18, 73. Лабораторная работа 11 (5) определение момента инерции колеса и момента силы трения

• Название: Лабораторная работа 11 (5) определение момента инерции колеса и момента силы трения
• Анкор: лабораторные работы
• Дата: 24.12.2022
• Размер: 340.97 Kb.
• Имя файла: Лабораторные работы 5, 18, 73.docx
• Тип: Лабораторная работа; #861966
• страница: 2 из 4

Вывод:

КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое движение твердого тела называется: а) поступательным, b) вращательным?

2. Сформулируйте основное уравнение динамики: а) поступательного движения, b) вращательного движения.

3. Каков физический смысл момента инерции и от чего он зависит?

4. Чему равен момент инерции: а) материальной точки, b) протяженного тела относительно произвольной оси вращения?

5. От каких величин зависит момент силы?

6. Чему равен момент силы тяжести колеса относительно оси вращения?

7. Какие силы, действующие на груз, не учтены в уравнении (6) и почему?

8. При каком условии колесо вращается с постоянной угловой скоростью? Как при этом движется груз? Какова при этом сила натяжения нити?

9. Какие величины в работе находятся путем прямых измерений, а какие  путем косвенных измерений?

Лабораторная работа № 2.6 (18)

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА

Цель работы: изучение первого закона термодинамики и теории теплоемкости идеального газа; измерение воздуха.

ТЕОРЕТИЧЕСКИЙ МИНИМУМ

Первый закон термодинамики

Количество теплоты , сообщенное системе, расходуется на приращение внутренней энергии системы и на совершение ею работы против внешних сил

. (1)

Соотношение (1) является частной формой закона сохранения энергии применительно к тепловым (термодинамическим) процессам.

Теплоемкостью тела называется физическая величина, численно равная количеству теплоты, которое надо сообщить телу, чтобы повысить его температуру на один градус. Если сообщение телу количества теплоты повышает его температуру на , то теплоемкость тела по определению равна

. (2)

Удельной теплоемкостью называется теплоемкость единицы массы вещества. Справедливо равенство , где – масса тела.

Молярной теплоемкостью называется теплоемкость одного моля вещества , где – молярная масса (масса моля).

Идеальным газом называется газ, молекулы которого не взаимодействуют между собой на расстоянии, суммарный объем молекул много меньше объема газа и взаимодействие молекул газа друг с другом и со стенками сосуда абсолютно упругое.

Теплоемкость идеального газа зависит от условий, при которых происходит нагревание газа. Если газ нагревается при постоянном объеме ( 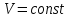), то это теплоемкость при постоянном объеме и обозначается (молярная теплоемкость ). Если газ нагревается при постоянном давлении ( ), то это теплоемкость при постоянном давлении и обозначается (молярная теплоемкость  ).

Молярные теплоемкости и связаны уравнением Майера

, (3)

где Дж/(моль·ּК) – универсальная газовая постоянная.

При нагреве газа в жестком замкнутом сосуде ( ) все передаваемое тепло, согласно (1), идет только на увеличение внутренней энергии газа: . Нагревая тот же газ в сосуде с подвижным поршнем (  ), будет наблюдаться не только увеличение температуры (или внутренней энергии) газа, но и его расширение, то есть совершение газом работы над внешними телами: . Поэтому во втором случае нужно затратить большее количество теплоты, чтобы нагреть газ на один градус, то есть .

Для идеального газа согласно классической теории теплоемкостей

, (4)

где – число степеней свободы молекулы газа.

Число степеней свободы молекулы – это минимальное число независимых координат, определяющих положение молекулы в пространстве. Для подсчета числа степеней свободы атомы в молекуле считают материальными точками. Если молекула одноатомная, то (три координаты , , ). Если молекула двухатомная и межатомное расстояние фиксировано¹, то (три координаты , , ) одного атома и два угла поворота ( , ) второго атома вокруг первого. «Жесткие» многоатомные молекулы аналогичны твердому телу, положение которого в пространстве описывается шестью координатами: три координаты ( , , ) центра масс молекулы и три угла поворота ( , , ) молекулы как целого вокруг центра масс, так что . Для линейных многоатомных молекул (например, для СО₂), у которых все атомы расположены вдоль одной линии, число степеней свободы .

Уравнение Клапейрона-Меделеева – это уравнение состояния идеального газа, которое имеет вид

, (5)

где , V, T, m, M – давление, объем, абсолютная температура, масса и молярная масса газа соответственно; – универсальная газовая постоянная.

Изопроцессы – это термодинамические процессы, при которых один из параметров состояния ( , или ) системы остается постоянным.

Изотермический процесс – процесс при постоянной температуре. Для идеального газа из (5) получаем (при неизменной массе): .

Изохорический процесс – процесс при постоянном объеме: .

Изобарический процесс – процесс при постоянном давлении: .

Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой.

Первый закон термодинамики для адиабатического процесса имеет вид: , поскольку . Это значит, что система может совершать работу над внешними телами за счет уменьшения своей внутренней энергии. Поэтому, например, охлаждается первоначально сжатый в баллоне газ при открывании баллона и резком уменьшении давления. За короткое время газ не успевает обменяться теплом с внешней средой (то есть процесс адиабатический), и работа по вытеснению газа совершается за счет внутренней энергии оставшегося в баллоне газа.

Адиабатический процесс для идеального газа описывается уравнением Пуассона

, (6)

где – показатель адиабаты. Учитывая (3) и (4), имеем

. (7)
МЕТОДИКА ЭКСПЕРИМЕНТА

Схема установки для определения величины воздуха методом Клемана-Дезорма изображена на рис. 1.

В стеклянный баллон Б насосом Н накачивается воздух. Если при накачивании воздуха давление в баллоне превышает некоторое максимальное значение , то срабатывает водный ограничитель О, который сбрасывает лишнее давление воздуха. (Величина задается глубиной погружения трубки в воду в ограничителе.) С помощью манометра М измеряется разность давлений воздуха в баллоне и в атмосфере, которая пропорциональна разности уровней жидкости в манометре. Кран К позволяет соединять баллон с насосом, с атмосферой или перекрывать баллон.

Рассмотрим сущность метода. Вначале открывается кран К и насосом в баллон накачивается воздух до некоторого давления и кран закрывается. Во время накачивания температура воздуха в баллоне несколько повышается. Через 2-3 минуты воздух в баллоне остывает, и его температура становится равной комнатной температуре. После установления термодинамического равновесия измеряется разность уровней жид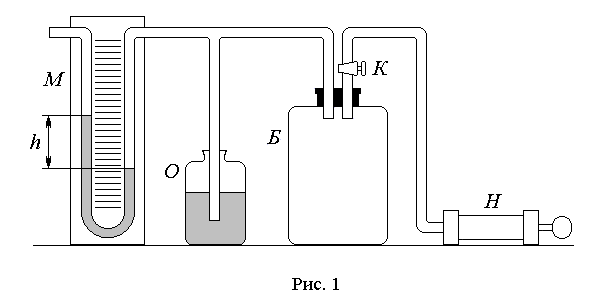кости в манометре. При этом давление воздуха в баллоне

, (8)

где – плотность жидкости в манометре (в нашем случае воды); – ускорение свободного падения; – разность уровней жидкости в манометре.





Затем на короткое время (на 1–2 секунды) вынимаем трубку из ограничителя, и баллон соединяется с атмосферой. В результате давление воздуха в баллоне быстро понижается и выравнивается с атмосферным давлением. Это показывает манометр М: уровни жидкости в обоих коленах манометра выравниваются. Быстрое понижение давления воздуха в баллоне можно считать адиабатическим процессом, поэтому при расширении воздух в баллоне охлаждается. После закрывания крана наблюдается постепенное увеличение давления воздуха в баллоне за счет увеличения его температуры до комнатной. После установления термодинамического равновесия вновь измеряется разность уровней 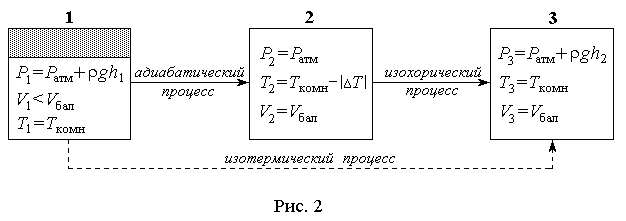жидкости в манометре. По значениям и можно рассчитать искомую величину отношения теплоемкостей .




А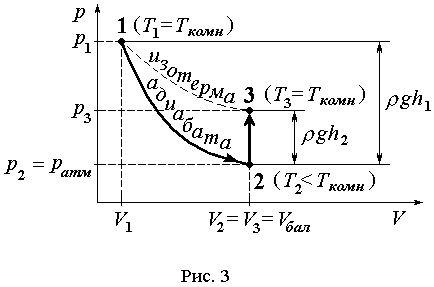
нализ происходящих во время выполнения работы процессов удобно провести не для всей массы воздуха в баллоне, а для той его части, которая остаётся в баллоне после того, как часть воздуха выпущена во время адиабатического расширения. Так как к концу эксперимента оставшийся в баллоне воздух занимает весь объем баллона , то до открывания крана эта масса газа занимала меньший объем . Таким образом, начальное состояние 1 рассматриваемой части газа характеризуется параметрами ( , , ). Состояние 1 изображено прямоугольником 1 на схеме процесса (рис. 2) и точкой 1 на -диаграмме (рис. 3).

Соединение баллона с атмосферой приводит к быстрому расширению газа от объема до объема . Давление в баллоне при этом падает от до . Рассматриваемый процесс можно считать адиабатическим, так как вследствие его кратковременности теплообмен между газом в баллоне и атмосферой не успевает произойти. При адиабатическом процессе работа по вытеснению газа совершается за счет внутренней энергии оставшегося в баллоне газа. Внутренняя энергия газа уменьшается, следовательно, уменьшается его температура от до .

Состояние 2 с параметрами ( , , ) изображено на рис. 2 и рис. 3 соответственно прямоугольником 2 и точкой 2. Переход между состояниями 1 и 2 описывается уравнением Пуассона для адиабатического процесса

. (9)

После адиабатического расширения баллон перекрывается и оставшийся в нем газ изохорически (то есть при постоянном объеме ) нагревается до комнатной температуры . При этом давление газа в баллоне повышается до значения

, (10)

где – установившаяся разность уровней жидкости в манометре после закрывания крана. Состояние 3 с параметрами ( , , ) изображено на рис. 2 и на рис. 3 соответственно прямоугольником 3 и точкой 3.

Состояниям 1 и 3 соответствует одинаковая температура²: . Следовательно, процесс перехода 1  3 можно рассматривать как изотермический, для которого справедливо равенство

. (11)

Подставив в уравнения (9) и (11) выражения (8) и (10), получим

(12)

Точное решение системы (12) относительно величины имеет вид

. (13)

Поскольку в нашем эксперименте , то, учитывая математическое соотношение: при , из формулы (13) находим расчетное выражение для отношения теплоемкостей

. (14)

Приборы и принадлежности: стеклянный баллон с краном, ограничитель давления; манометр; насос.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

№	, мм	, мм
1	75	20
2	73	24
3	73	17
4	73	26
5	71	24

7. Для каждого опыта по формуле (14) рассчитайте экспериментальные значения и найдите среднее значение . Полученные значения запишите в табл. 1.

8. Рассчитайте погрешность эксперимента по формуле

,

где ; , .

Для определения абсолютной погрешности найдите приборную погрешность манометра (равна цене деления манометра) и случайную погрешность измерений . В качестве погрешности выберите наибольшую из них. Погрешность определяется аналогично.

Окончательный результат измерения отношения теплоемкостей запишите в виде доверительного интервала

.

9. Воздух – это смесь в основном трех газов: азота (78 % по объему), кислорода (21 %) и углекислого газа (0,03 %), молекулы которых имеют одинаковое число степеней свободы = 5 (смотрите с. 25). Учитывая это, по формуле (7) рассчитайте теоретическое значение .

10. Сделайте вывод о совпадении теории с экспериментом, сопоставив теоретическое значение отношения теплоемкостей и экспериментальный доверительный интервал .

11. Рассчитайте, насколько уменьшается температура воздуха в баллоне в результате адиабатического расширения. Это можно сделать двумя способами, рассматривая адиабатический процесс 1  2 или изохорический процесс 2  3 (рис. 2). В первом случае необходимо использовать связь давления и температуры для адиабатического процесса: . Во втором случае – уравнение изохорического процесса: . Cогласно рис. 2 получаем для адиабатического процесса

, (15)

для изохорического процесса

. (16)

(Способ расчета изменения температуры указывает преподаватель).

Комнатную температуру t_К измерьте с помощью термометра в лаборатории и переведите полученный результат в абсолютную температуру

Т _комн = (t_К + 273) К. (17)

Атмосферное давление примите равным  Па. Плотность манометрической жидкости (воды)  кг/м³;  м/с². В качестве величин и (в метрах) используйте результаты измерения, например, первого опыта. Значение примите равным экспериментальному значению .
Вывод: измерили _____________________________ методом _______________________: ; табличное значение ___________________ в полученный доверительный интервал; рассчитали, что температура воздуха в баллоне в результате адиабатического расширения уменьшается на ____________________.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сформулируйте первый закон термодинамики.

2. Что такое: a) теплоемкость тела; б) удельная теплоемкость; в) молярная теплоемкость?

3. Что такое: a) теплоемкость при постоянном объеме; б) теплоемкость при постоянном давлении? Какая из них больше и почему?

4. Что такое число степеней свободы молекулы? Чему равно число степеней свободы для молекул азота , кислорода , углекислого газа ?

5. Что такое адиабатический процесс? Почему в данной работе процесс расширения газа при открывании крана можно считать адиабатическим?

6. Как и почему меняется температура газа при адиабатическом расширении?

7. Чему равен показатель адиабаты в уравнении Пуассона (6)?

8. Поясните, что характеризует объем на рисунках 2 и 3.

9. Поясните причину повышения давления в баллоне сразу после адиабатического расширения газа и закрывания крана.

Лабораторная работа 3.1 (73)

ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ

И ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ
Цель работы: изучение принципа действия и характеристик основных электроизмерительных приборов; проверка закона Ома; измерение удельного сопротивления проводника.
ТЕОРЕТИЧЕСКИЙ МИНИМУМ

Электроизмерительные приборы классифицируются:

• 
  по виду измеряемой физической величины – амперметры, вольтметры, омметры и др.;
  
• 
  по роду тока – приборы постоянного тока, приборы переменного тока, приборы постоянного и переменного тока;
  
• 
  по принципу действия – магнитоэлектрические, электромагнитные, электродинамические, тепловые и др.;
  
• 
  по степени точности – зависит от класса точности.
  

Основные признаки прибора обозначаются условными знаками и приводятся на шкале прибора.

Наименование символа	Обозначение
Прибор постоянного тока
Прибор переменного тока
Прибор постоянного и переменного тока
Прибор магнитоэлектрической системы
Прибор электромагнитной системы
Установка прибора вертикальная
Установка прибора горизонтальная
Класс точности (например, 1,5)
Пробивное напряжение изоляции (например, 2 кВ)
Измерительная цепь изолирована от корпуса и проверена напряжением (например, 2 кВ)

Вид измеряемой величины

Величина, измеряемая прибором, указывается в виде обозначения единицы измерения, в которых отградуирован прибор.

В физическом практикуме электроизмерительные приборы используются в основном для измерения силы тока и напряжения. Для измерения силы тока применяются амперметры ( ), миллиамперметры ( ) имикроамперметры (  ), а для измерения напряжения – вольтметры ( ) или милливольтметры (  ).

Результаты измерений следует записывать русскими символами:

А – ампер, мА – миллиампер, мкА – микроампер, В – вольт, мВ – милливольт.

Система прибора

Любой электроизмерительный прибор состоит из подвижной и неподвижной части. По величине перемещения подвижной части (чаще всего стрелки) судят о величине измеряемого тока, напряжения и т.д.

Конструкция прибора определяется в первую очередь принципом работы и назначением прибора и зависит от устройства его измерительного механизма. В данном лабораторном практикуме рассматривается устройство и принцип работы двух наиболее распространенных систем.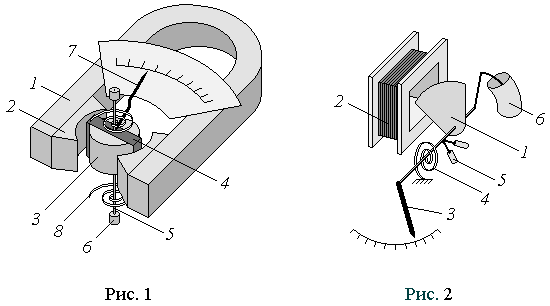





Принцип работы приборов магнитоэлектрической системы (рис. 1) основан на взаимодействии магнитного поля постоянного магнита и обмотки подвижной части прибора, по которой протекает измеряемый ток. Между наконечниками 2 постоянного магнита 1 неподвижно укреплен стальной цилиндрический сердечник 3, в зазоре между которыми находится подвижная рамка 4 с обмоткой из тонкого провода. На торцевых сторонах катушки укреплены полуоси 5, упирающиеся в подпятники 6. На одной полуоси закреплена стрелка 7. Конец стрелки может перемещаться над шкалой с делениями. Две спиральные пружины 8 служат для электрического соединения обмотки с внешней цепью и для создания противодействующего момента силы.

Магнитоэлектрические приборы применяются для измерения тока и напряжения только в цепях постоянного тока. Они имеют равномер­ную шкалу, обладают большой точностью и чувствительностью.

Принцип работы приборов электромагнитной системы (рис. 2) основан на взаимодействии ферромагнитного сердечника подвижной части измерительного механизма с магнитным полем тока, протекающим в неподвижной катушке. На оси подвижной части этого прибора закрепле­на плоская стальная пластина 1 специальной формы, втягиваемая внутрь неподвижной катушки 2, по которой проходит измеряемый ток. С осью сердечника связана стрелка-указатель 3 и спиральная пружина 4. Грузики 5 служат для уравновешивания подвижной части измерительного механизма. Для успокоения стрелки прибора применяется воздушный поршневой успокоитель 6.

Приборы этого типа просты по устройству, дешевы и прочны, поэтому нашли широкое применение главным образом для технических измерений переменного тока промышленной частоты.

Недостатком электромагнитных приборов является их малая чув­ствительность, низкая точность и неравномерность шкалы.

Пределы измерений

З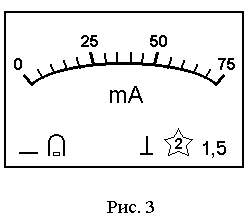
начение измеряемой величины, при котором стрелка прибора откло­няется до конца шкалы, называется пределом измерения этого прибора. В простейшем случае предел измерений указывается градуировкой шкалы прибора. Для примера на рис. 3 изображена шкала миллиамперметра магнитоэлектрической системы с пределом измерения 75 мА.
Электроизмерительные приборы могут иметь несколько пределов измерения (так называемые многопредельные приборы). В этом случае на шкале указывается наименование измеряемой величины, а предел измерения указывается на переключателе или рядом с соответствующей клеммой. Например, если вольтметр имеет два предела измерения 3 В и 7,5 В, то на его шкале может быть нанесено 75 делений, а на переключателе указано 3 V и 7,5 V.

Цена деления

Цена деления прибора равна значению измеряемой величины, которое соответствует одному делению шкалы. Если шкала прибора имеет Nделений, аего предел измерения Х_т, то цена деления такого прибора

. (1)

Формулу (1) можно применять только для приборов магнитоэлектрической системы с равномерной шкалой.

Цена деления прибора, изображенного на рис. 3, равна 5 мА/дел.

Умногопредельных приборов цена деления для разных пределов измерений различна. Например, если вольтметр имеет два предела измерения: 3 В и 7,5 В, а шкала прибора имеет 75 деле­ний, то цена деления

для предела 3 В с = 3В/75 дел = 0,04 В/дел.;

для предела 7,5 В с = 7,5В/75 дел = 0,1 В/дел.
Класс точности и приборные погрешности

Приборные погрешности измерений зависят от класса точности прибора. Электроизмерительные приборы делятся на 8 классов точности: 0,05; 0,1;0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Числа, определяющие класс точности прибора, указывают на то, что систематическая абсолютная погрешность прибора в любом месте шкалы не долж­на превышать соответственно 0,05; 0,1; 0,2; 0,5; 1,0;1,5; 2,5; 4,0 процента от предела измерения прибора.

Если – класс точности прибора, а предел его измерения , то абсолютная приборная погрешность определяется по формуле

. (2)

Формула (2) показывает, что приборная абсолютная погрешность зависит не от значения измеряемой величины, а только от класса точности прибора и его предела измерения. Она имеет одно и то же значение в пределах всей шкалы.

Приборная относительная погрешность определяется как отношение абсолютной погрешности к найденному значению измеряемой величины

. (3)

Подставляя в формулу (3) значение (2), получим

. (4)
Таким образом, относительная погрешность электроизме­рительного прибора зависит от значения измеряемой величины и тем больше, чем меньше измеряемая величина. Для уменьшения относительной приборной погрешности необходимо пользоваться приборами, пределы измерения которых близки к значениям измеряемых величин. При точных измерениях измеряемые величины должны составлять не менее 70…80 % от предела измерения прибора.