Лабораторные по физике. лабораторные. Лабораторная работа 11 (5) определение момента инерции колеса и момента силы трения
 Скачать 397.53 Kb. Скачать 397.53 Kb.
|
|
Лабораторная работа № 1.11 (5) ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ КОЛЕСА И МОМЕНТА СИЛЫ ТРЕНИЯ Цель работы: изучение динамики поступательного и вращательного движений твердого тела. измерение момента инерции колеса и момента силы трения. Краткая теория Момент инерции характеризует инертность тела при вращательном движении подобно тому, как масса характеризует инертность тела при поступательном движении. Моментом инерции материальной точки относительно оси вращения называется произведение массы m точки на квадрат ее расстояния r до оси 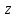 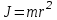 . (1) . (1)Момент инерции системы  материальных точекотносительно оси материальных точекотносительно оси 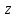 равен сумме моментов инерции всех материальных точек системы равен сумме моментов инерции всех материальных точек системы  , (2) , (2)где 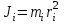 – момент инерции i-й материальной точки относительно оси – момент инерции i-й материальной точки относительно оси 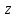 . .Момент инерции тела относительно оси 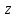 при непрерывном распределении массы по объему тела определяется предельным переходом от суммы в выражении (2) к интегралу при непрерывном распределении массы по объему тела определяется предельным переходом от суммы в выражении (2) к интегралу 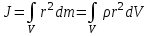 , (3) , (3)где r – расстояние от элементарной массы dm (или от элемента объема dV) до оси 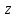 ; ;  – плотность вещества. Интегрирование ведется по всему объему V тела. – плотность вещества. Интегрирование ведется по всему объему V тела.Из (1)–(3) следует, что момент инерции зависит от распределения массы относительно оси вращения. А именно: чем дальше масса удалена от оси, тем больше момент инерции, тем труднее заставить тело вращаться или остановить уже вращающееся тело. Моментом силы относительно точки О называется векторная величина 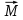 , равная векторному произведению радиус-вектора , равная векторному произведению радиус-вектора 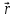 , проведенного из точки О в точку приложения силы, на вектор силы , проведенного из точки О в точку приложения силы, на вектор силы 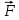 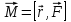 . (1) . (1)Моментом силы относительно оси Z, проходящей через точку О, называется скалярная величина 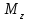 , равная проекции вектора , равная проекции вектора 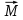 на ось на ось 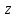 . . Основной закон динамики поступательного движения твердого тела выводится из второго закона Ньютона для материальной точки и имеет вид 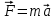 , (3) , (3)где 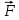 – сумма внешних сил, действующих на тело (результирующая сила), – сумма внешних сил, действующих на тело (результирующая сила), 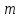 – масса тела, – масса тела, 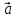 – ускорение центра масс тела (в инерциальной системе отсчета). – ускорение центра масс тела (в инерциальной системе отсчета).Основной закон динамики вращательного движения твердого тела вокруг неподвижной (в инерциальной системе отсчета) оси имеет вид  , (4) , (4)где 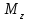 сумма моментов внешних сил, действующих на тело, относительно оси вращения (результирующий момент сил); сумма моментов внешних сил, действующих на тело, относительно оси вращения (результирующий момент сил); 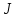 момент инерции тела относительно оси вращения; момент инерции тела относительно оси вращения;  угловое ускорение тела. угловое ускорение тела.Закон сохранения механической энергии Механическая энергия консервативной системы сохраняется (т.е. не изменяется с течением времени). Закон сохранения механической энергии имеет вид: 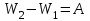 , (5) , (5)где 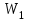 , , 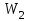 – механическая энергия системы в моменты времени – механическая энергия системы в моменты времени 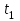 и и  ( ( ); );  – работа диссипативных сил за время – работа диссипативных сил за время  . Так как . Так как 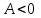 , то , то  . . В консервативной системе 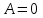 и и 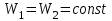 . .Механическая энергия – это сумма кинетической и потенциальной энергий тел, входящих в систему. Экспериментальная часть
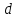 = 52,0 мм , = 52,0 мм ,  = 2,4 кг , = 2,4 кг , 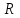 = 10 см = 10 смa1=2·1,45/3,1322 =0,296 м/с2 a1=2·1,35/2,6462 =0,386 м/с2 J=d2(m2-m1)g/4(a2-a1) = 0,0522(0,7-0,5) ·10/4(0,386-0,296) = 0,015 кг·м2 Погрешность ∆J = εJэкс , учитывая только погрешности измерения времени:   εt1 = 2·2,6462·0,08/3,132· (3,1322 -2,6462) = 0,127  εt2 = 2·3,1322·0,07/2,646· (3,1322 -2,6462) = 0,127 ε=√( εt12 + εt22 ) ε =0,22 ∆J = εJэкс= 0,22*0,015 = 0,0033 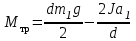 = -0,041 Н*м = -0,041 Н*мВывод: наблюдали поступательное движение груза и вращательное движение махового колеса; определили момент инерции махового колеса и момент силы трения в подшипнике: J= (0.015 + 0.003) кг·м2 , Мтр = -0,041 Н·м; основной вклад в ошибку измерения момента инерции внесла погрешность измерения времени движения груза большей массы, из-за ограниченности скорости реакции при остановке секундомера. Лабораторная работа № 2.6 ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ Цель работы: изучение первого закона термодинамики и теории теплоемкости идеального газа; измерение Краткая теория: Первый закон термодинамики Количество теплоты Соотношение (1) является частной формой закона сохранения энергии применительно к тепловым (термодинамическим) процессам. Теплоемкостью тела называется физическая величина, численно равная количеству теплоты, которое надо сообщить телу, чтобы повысить его температуру на один градус. Если сообщение телу количества теплоты Удельной теплоемкостью Молярной теплоемкостью Идеальным газом называется газ, молекулы которого не взаимодействуют между собой на расстоянии, суммарный объем молекул много меньше объема газа и взаимодействие молекул газа друг с другом и со стенками сосуда абсолютно упругое. Теплоемкость идеального газа зависит от условий, при которых происходит нагревание газа. Если газ нагревается при постоянном объеме ( 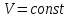 ), то это теплоемкость при постоянном объеме и обозначается ), то это теплоемкость при постоянном объеме и обозначается Молярные теплоемкости где Число степеней свободы молекулы – это минимальное число независимых координат, определяющих положение молекулы в пространстве. Уравнение Клапейрона-Меделеева – это уравнение состояния идеального газа, которое имеет вид где Изопроцессы – это термодинамические процессы, при которых один из параметров состояния ( Изотермический процесс – процесс при постоянной температуре. Для идеального газа из (5) получаем (при неизменной массе): Изохорический процесс – процесс при постоянном объеме: Изобарический процесс – процесс при постоянном давлении: Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой. Первый закон термодинамики для адиабатического процесса имеет вид: Адиабатический процесс для идеального газа описывается уравнением Пуассона где Экспериментальная часть
 , , εh1 = 22,2*2/73(73-22,2) = 0,012  εh2 = 3,5/73-22,2 = 0,069 ε = 0,07 ∆γ = 0,07*1,442 = 0,101 γ = 1,442± 0,101 γтеор = i+2/i γтеор = 1,4 Можем сделать вывод, что γтеор и γэксп практически совпадают. Рассмотрим изохорический процесс 2 3. Уравнение изохорического процесса:  . .Т комн = (tК + 273) К Т комн = 21+273 = 294К ∆T = 294(1-(105/105+200)) = 0,587 g=9,8 м/с2 h2 = 20 мм Вывод: измерили отношение теплоёмкостей методом Клемана-Дезорма: Лабораторная работа 3.1 ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ И ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ Цель работы: изучение принципа действия и характеристик основных электроизмерительных приборов; проверка закона Ома; измерение удельного сопротивления проводника. Краткая теория: Электроизмерительные приборы классифицируются: по виду измеряемой физической величины – амперметры, вольтметры, омметры и др.; по роду тока – приборы постоянного тока, приборы переменного тока, приборы постоянного и переменного тока; по принципу действия – магнитоэлектрические, электромагнитные, электродинамические, тепловые и др.; по степени точности – зависит от класса точности. Основные признаки прибора обозначаются условными знаками и приводятся на шкале прибора. Система прибора Любой электроизмерительный прибор состоит из подвижной и неподвижной части. По величине перемещения подвижной части (чаще всего стрелки) судят о величине измеряемого тока, напряжения и т.д. Конструкция прибора определяется в первую очередь принципом работы и назначением прибора и зависит от устройства его измерительного механизма. 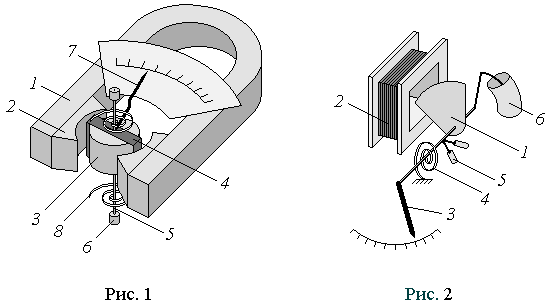 Принцип работы приборов магнитоэлектрической системы (рис. 1) основан на взаимодействии магнитного поля постоянного магнита и обмотки подвижной части прибора, по которой протекает измеряемый ток. Магнитоэлектрические приборы применяются для измерения тока и напряжения только в цепях постоянного тока. Они имеют равномерную шкалу, обладают большой точностью и чувствительностью. Принцип работы приборов электромагнитной системы (рис. 2) основан на взаимодействии ферромагнитного сердечника подвижной части измерительного механизма с магнитным полем тока, протекающим в неподвижной катушке. Недостатком электромагнитных приборов является их малая чувствительность, низкая точность и неравномерность шкалы. Пределы измерений Значение измеряемой величины, при котором стрелка прибора отклоняется до конца шкалы, называется пределом измерения этого прибора. Электроизмерительные приборы могут иметь несколько пределов измерения (так называемые многопредельные приборы). В этом случае на шкале указывается наименование измеряемой величины, а предел измерения указывается на переключателе или рядом с соответствующей клеммой. Цена деления Цена деления прибора равна значению измеряемой величины, которое соответствует одному делению шкалы. Если шкала прибора имеет Nделений, аего предел измерения Хт, то цена деления такого прибора  . (1) . (1)Формулу (1) можно применять только для приборов магнитоэлектрической системы с равномерной шкалой. Умногопредельных приборов цена деления для разных пределов измерений различна. Класс точности и приборные погрешности Приборные погрешности измерений зависят от класса точности прибора. Электроизмерительные приборы делятся на 8 классов точности: 0,05; 0,1;0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Числа, определяющие класс точности прибора, указывают на то, что систематическая абсолютная погрешность прибора в любом месте шкалы не должна превышать соответственно 0,05; 0,1; 0,2; 0,5; 1,0;1,5; 2,5; 4,0 процента от предела измерения прибора. Если  . (2) . (2)Формула (2) показывает, что приборная абсолютная погрешность зависит не от значения измеряемой величины, а только от класса точности прибора и его предела измерения. Она имеет одно и то же значение в пределах всей шкалы. Приборная относительная погрешность Подставляя в формулу (3) значение (2), получим Экспериментальная часть: 1.
2. 3. L = 25 см ΔL = 0,1 см R = Uv/IA = 0,1 В/ 0,060А = 1,67 Ом << 2500 Ом, Следовательно, выбираем схему «а». 4. Таблица 2
5.   U, В U, В6.  . .d = 0,5 мм Δd = 0,01 мм  =1,005 (Ом·мм2/м) =1,005 (Ом·мм2/м)Можем сделать вывод, что Рассчитали погрешность определения удельного сопротивления где относительная погрешность удельного сопротивления Относительные частные погрешности  =0,015/1,5 = 0,01 ; =0,015/1,5 = 0,01 ;  =15/250= 0,06; =15/250= 0,06; =2*0,0/0,5 = 0,04. =2*0,0/0,5 = 0,04.Вывод: изучили принцип действия и характеристики основных электроизмерительных приборов; сняли вольтамперную характеристику металлического проводника, она получилась линейной, следовательно, закон Ома для участка цепи I = U/R ; измерили удельное сопротивление проводника | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

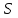 , м
, м , с
, с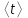 , с
, с , м/с2
, м/с2