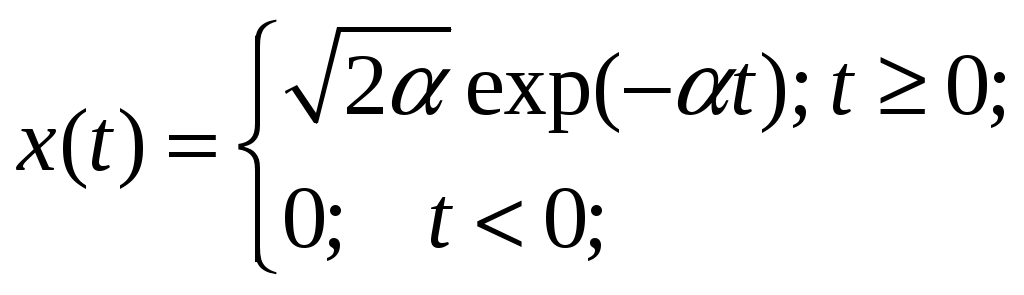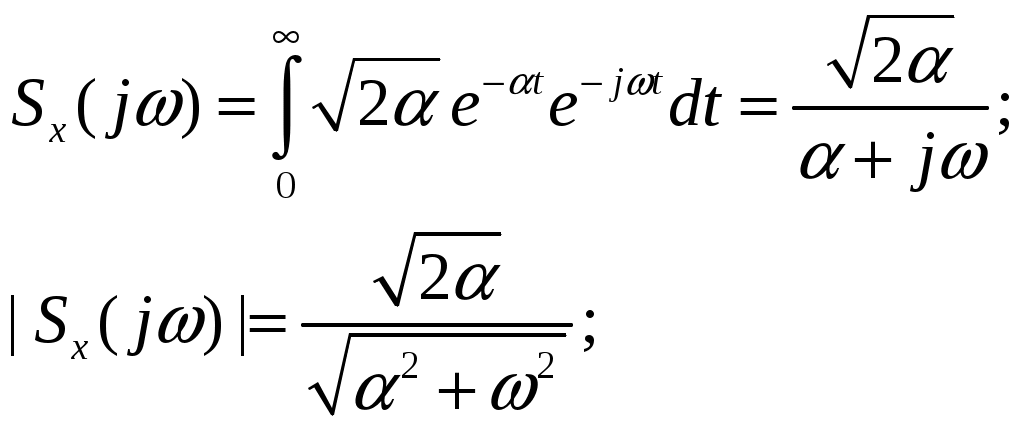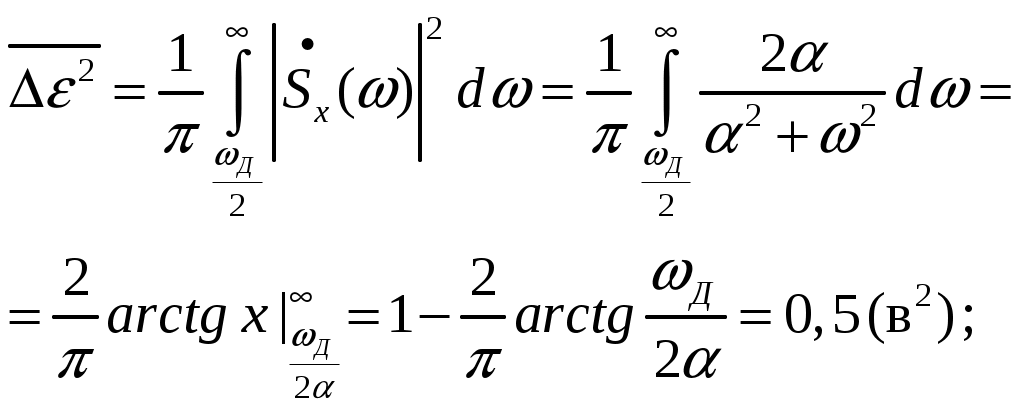ЛАБОРАТОРНАЯ РАБОТА №11
«Дискретизация и восстановление непрерывных сигналов»
1. Цель работы: Теоретическое и экспериментальное изучение временной дискретизации непрерывных сигналов, способов восстановления исходной функции по ее отсчетам и факторов, влияющих на точность восстановления.
2. ДОМАШНЕЕ ЗАДАНИЕ.
Вариант №15. Исходные данные к расчету:
-период следования отсчетных импульсов: t =10,0 мс;
-длительность импульсов: =0,5t;
-частота среза идеального ФНЧ: в=2π102рад/с;
-спектр исходной непрерывной функции Sx(), где 1= π/t [рад/c];
Sx()
-1 1
- R1=2кОм ; С1 =2мкФ ; = π/t [рад/c];
2.1. Структурная схема лабораторного макета показана на рис.1.

Рис.1.
2.2. Временная диаграмма одиночного - импульса имеет вид:
 u(t) u(t)
(t-a)
0 a t
Рис. 2.
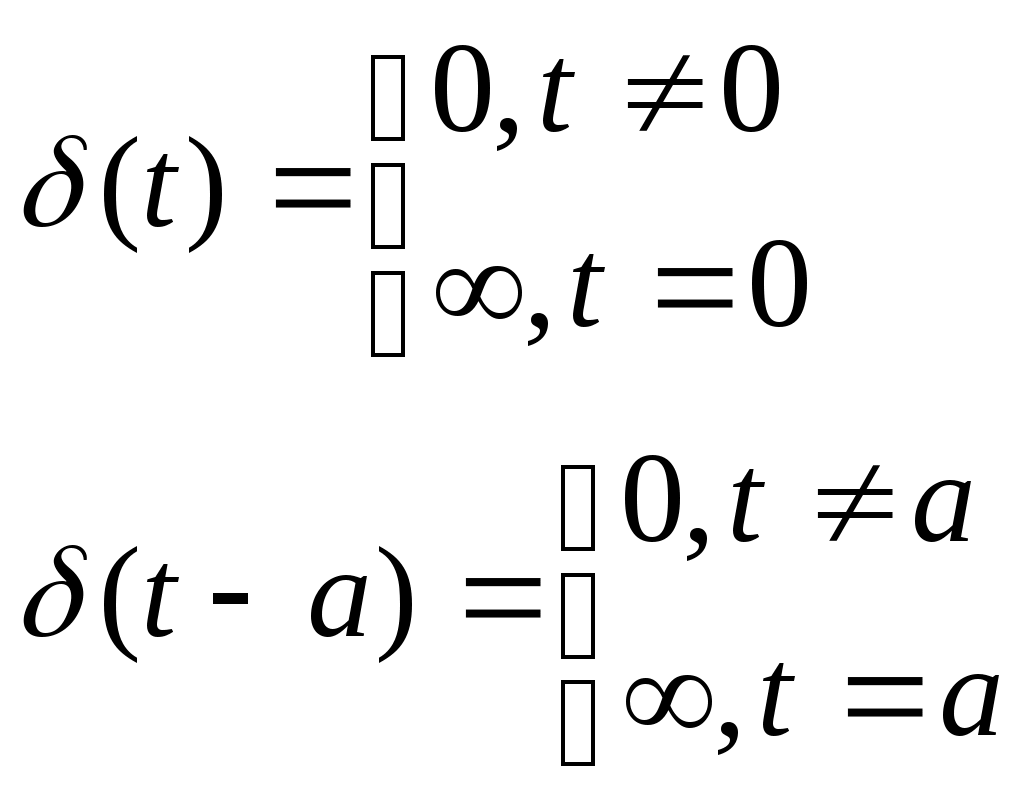
Спектр одиночного  - импульса получим, используя преобразование Фурье: - импульса получим, используя преобразование Фурье:
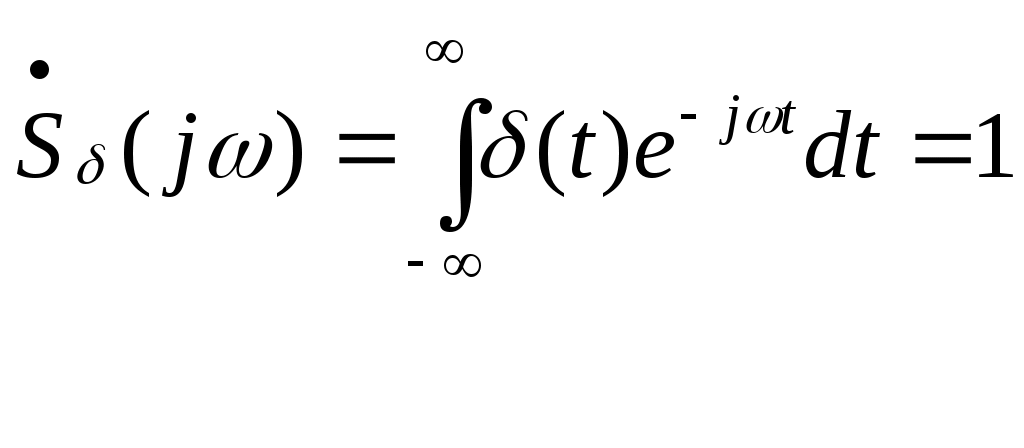
Использовано "фильтрующее" свойство дельта-функций:
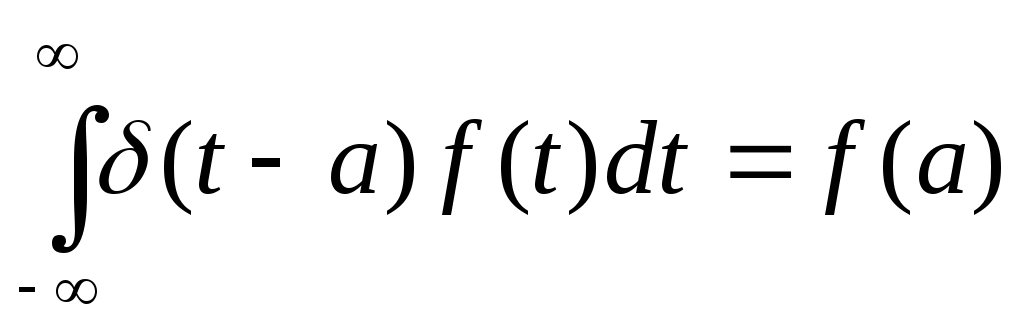
Следовательно, спектр одиночного дельта-импульса имеет вид:
 S(j) S(j)
1
Рис. 3.
2.3. Временная диаграмма периодической последовательности дельта-импульсов с периодом Т=t =10мс имеет вид:
 u(t) u(t)
t =10мс
.. (t+3t) (t+2t) (t+t) (t) (t-t) (t-2t) (t-3t) ……….
4t -3t -2t -t 0 t 2t 3t 4t t
Рис.4.
Так как сигнал периодический, то его спектр будет дискретным.
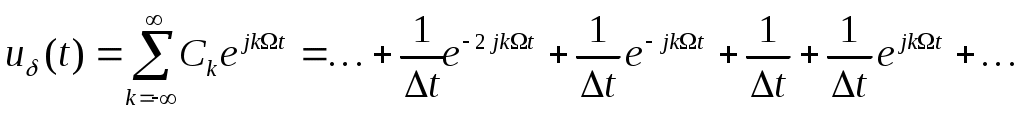
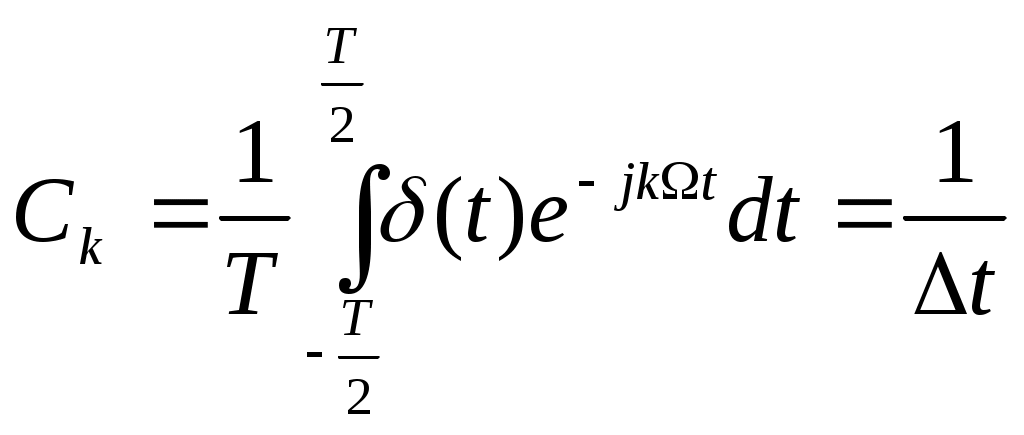 ; ; 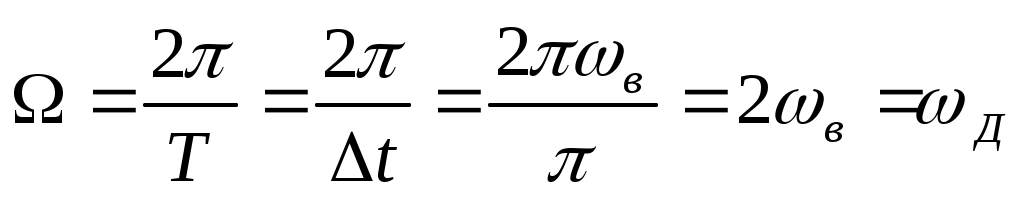
Т = t ;
Д = 6,28 102 (рад/с) - частота дискретизации.
Ск=1/ t = 102 (1/с);
Спектр периодической последовательности 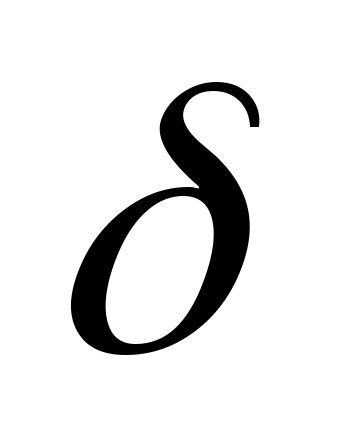 - импульсов в соответствии с формулой для uδ (t) имеет следующий вид : - импульсов в соответствии с формулой для uδ (t) имеет следующий вид :
S(j) 
1/t Д = 6,28 102 (рад/с)
--3д -2д -д 0 д 2д 3 д
Рис.5.
2.4.а. Спектр дискретизированного сигнала имеет следующий вид: 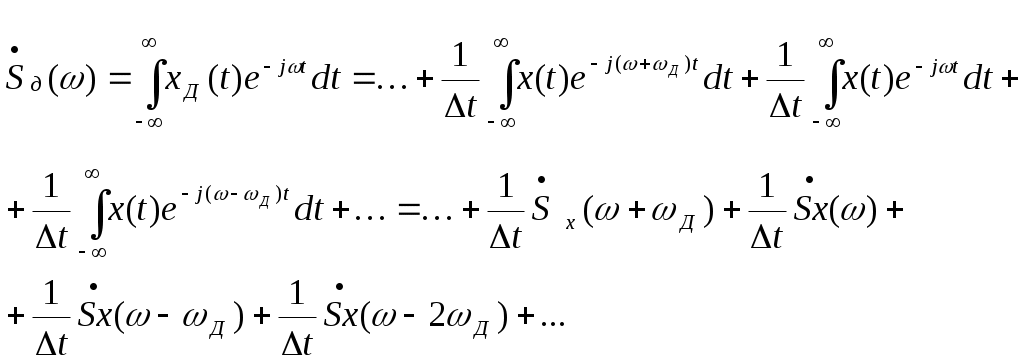
Т.о. мы видим, что спектр дискретизированного сигнала содержит спектр исходного сигнала Sx(), спектр исходного сигнала смещенный на величину частоты дискретизации вправо Sx( - д), тот же спектр смещенный на величину частоты дискретизации влево Sx(+ д), тот же спектр смещенный на величину 2д и т.д.
Спектр исходного непрерывного сигнала.
 Sx() Sx()
1 = 3,14 102 (рад/с)
-1 1
С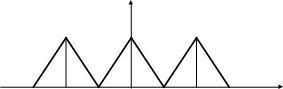 пектр дискретизированного сигнала: пектр дискретизированного сигнала:
Sд()
Д = 6,28 102 (рад/с);
1 = 3,14 102 (рад/с):
……….. …………
(-д - 1) - д - 1 0 1 д (д + 1)
Рис.6.
2.4.б. Спектр дискретизированного сигнала при дискретизации импульсами конечной длительности (сигнал амплитудно-импульсной модуляции или АИМ сигнал).
Спектр АИМ сигнала похож на спектр дискретизированного сигнала при дискретизации дельта-импульсами , но амплитуда составляющих спектра убывает с ростом номера гармоники:
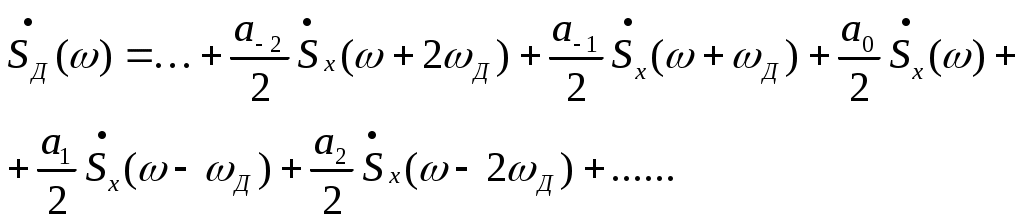
Коэффициенты ак – это коэффициенты разложения в ряд Фурье периодической последовательности прямоугольных импульсов:
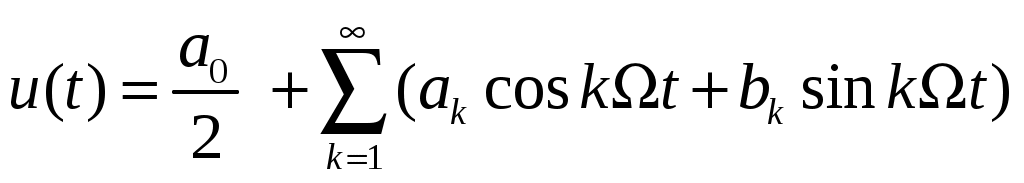
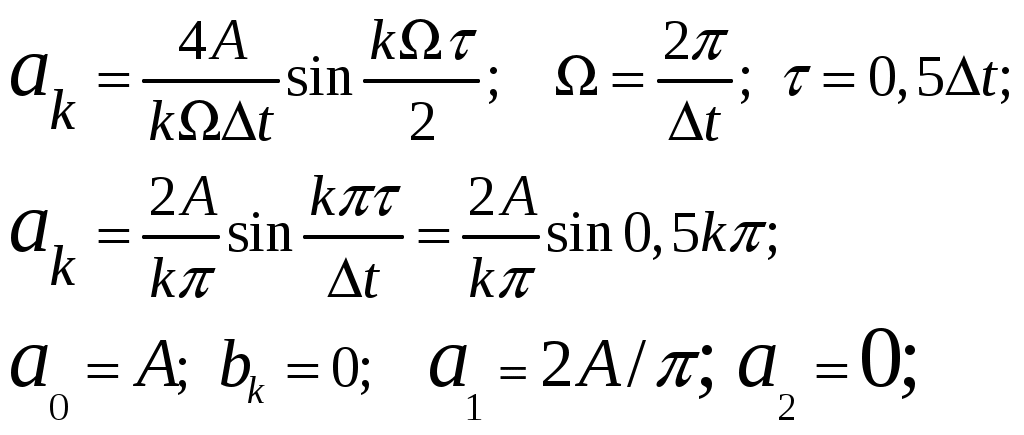
Спектр АИМ сигнала условно показан на рис. 7.
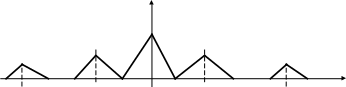 Sд() Sд()
Д = 6,28 102 (рад/с);
1 = 3,14 102 (рад/с):
-3д - д - 1 0 1 д 3д
Рис.7.
2.5. Амплитудно-частотная характеристика идеального ФНЧ (АЧХ ИФНЧ) имеет вид:
   K() K()
K0
в = 6,28 102 (рад/с);
- в 0 в
Рис.8.
Импульсная реакция ИФНЧ, т.е. реакция на дельта-импульс имеет вид:
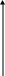 gифнч (t) gифнч (t)
t=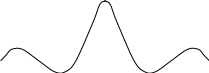 10мс; 10мс;
 t t
-3 t - 2t -t 0 t 2t 3t
Рис. 9.
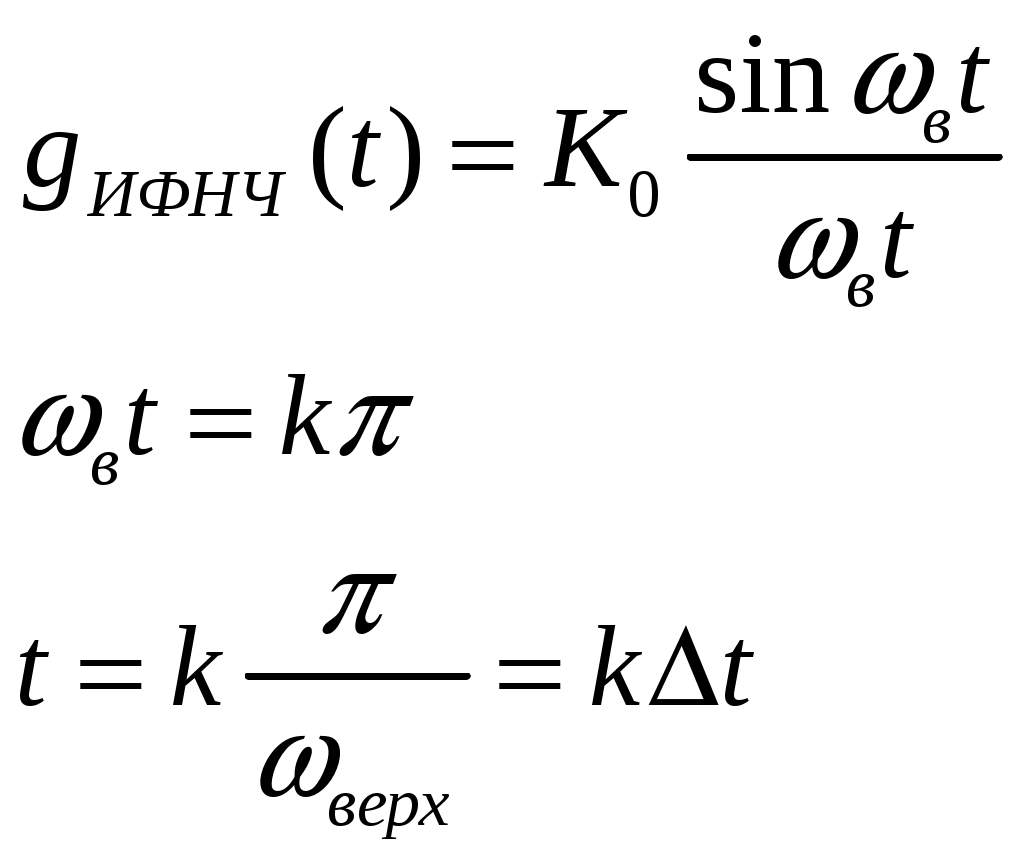
Первая формула - это выражение для импульсной реакции ИФНЧ, вторая и третья формулы определяют моменты времени, для которых g ИФНЧ(t) обращается в ноль.
2.6. Амплитудно-частотная характеристика RC ФНЧ имеет вид:
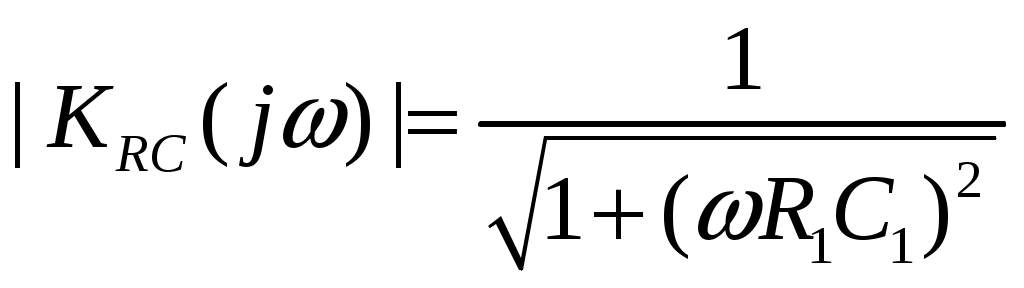
На рис.10 показана АЧХ RC ФНЧ.
|K(j)|
1 R1C1 =410-3 (с)
0 1/R1C1 2/R1C1 3/R1C1 4/R1C1
Рис.10.

Импульсная реакция RC-фильтра равна:
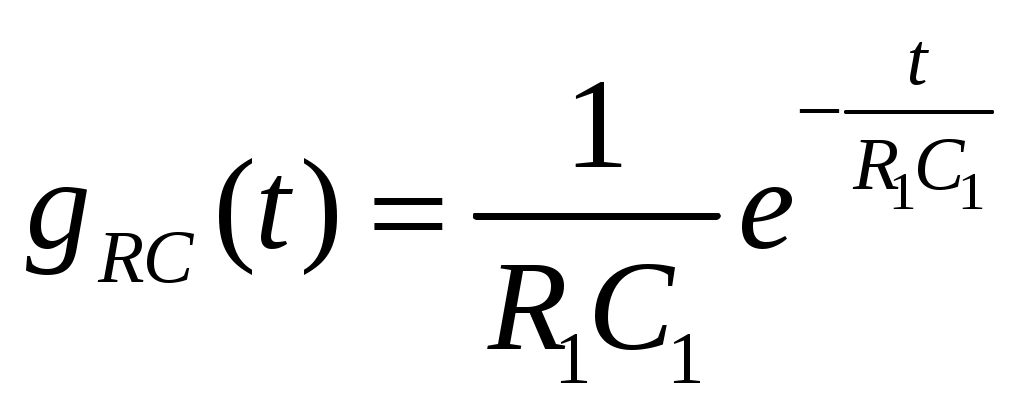 ; ;
На рис.11 показана импульсная реакция RC-фильтра:
 gRC(t) gRC(t)
250 R1C1 =410-3 (с)
t
0 R1C1 2 R1C1 3R1C1 4R1C1
Рис.11.
2.7. Расчет среднеквадратической погрешности восстановления исходного непрерывного сигнала, возникающей из-за того, что спектр непрерывного сигнала - бесконечен (погрешность фильтрации ).
Т.к. заданный сигнал имеет вид:
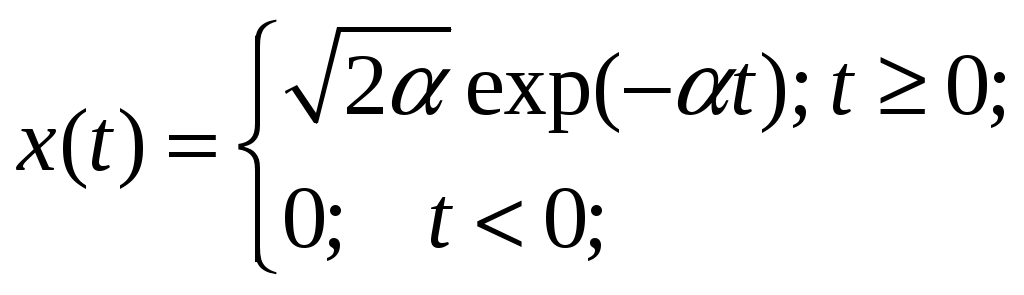
то его спектр определим в соответствии с преобразованием Фурье:
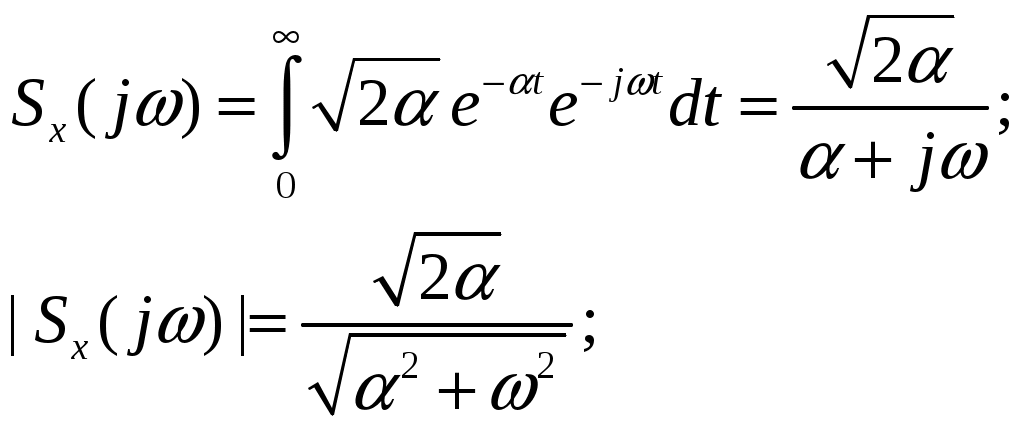
Среднеквадратическая погрешность восстановления сигнала равна, при условии, что =π/t ; ωД=2π/t:
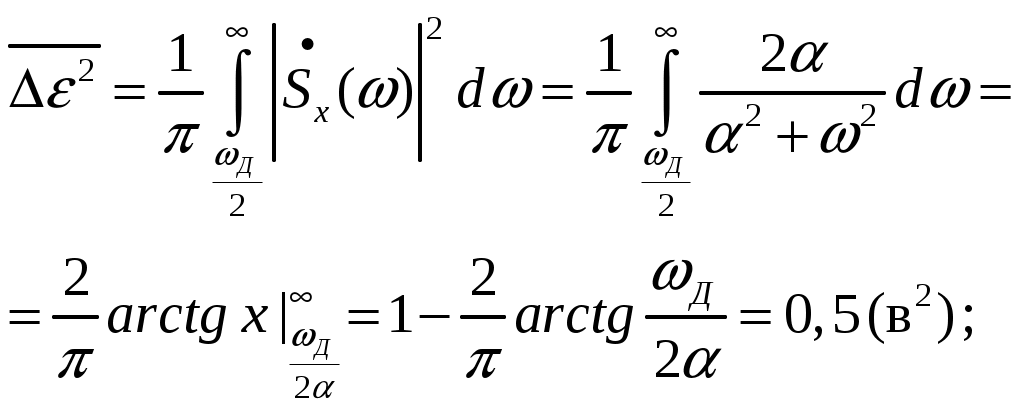
Э К С П Е Р И М Е Н Т. |
 Скачать 0.53 Mb.
Скачать 0.53 Mb.

 u(t)
u(t)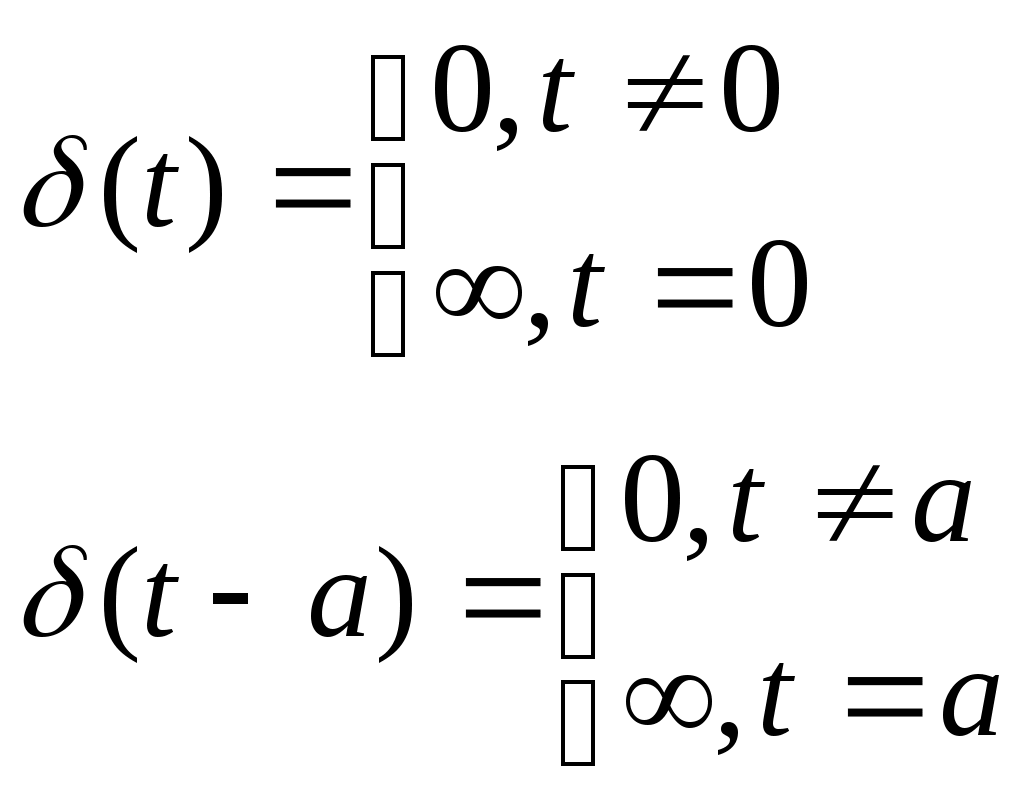
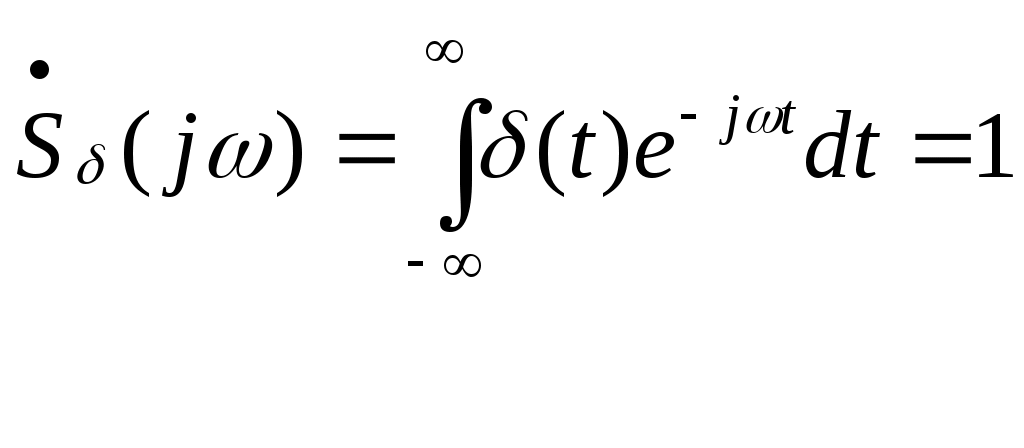
 S(j)
S(j) u(t)
u(t) 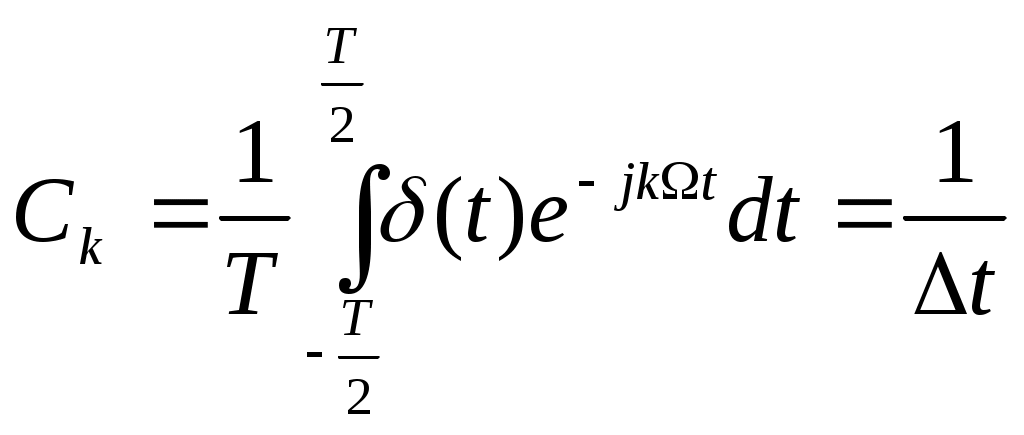 ;
; 

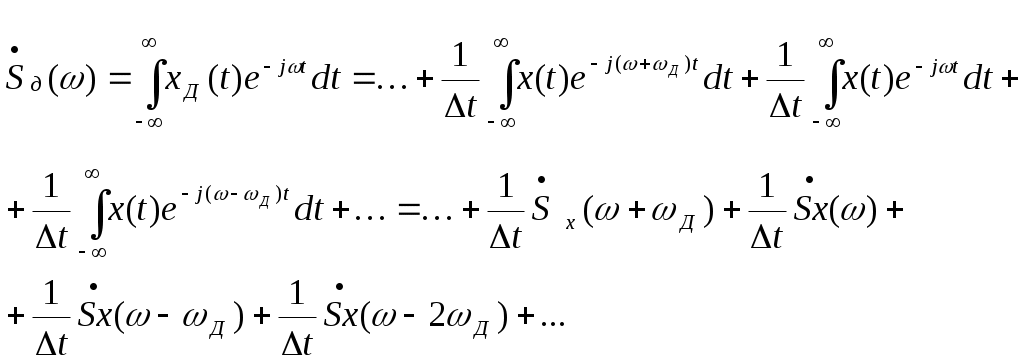
 пектр дискретизированного сигнала:
пектр дискретизированного сигнала: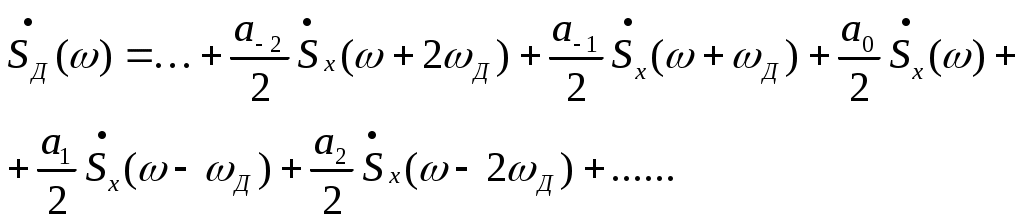
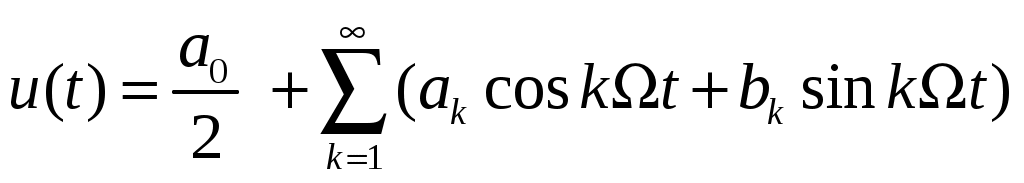
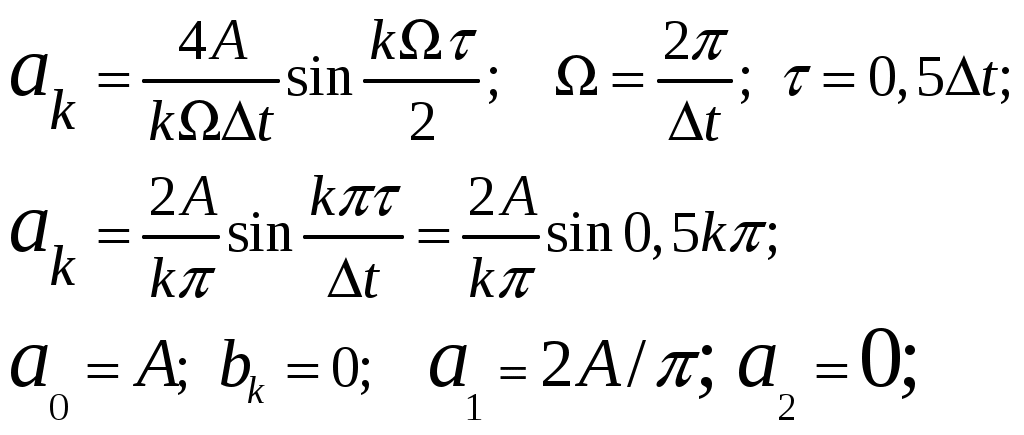



 10мс;
10мс; t
t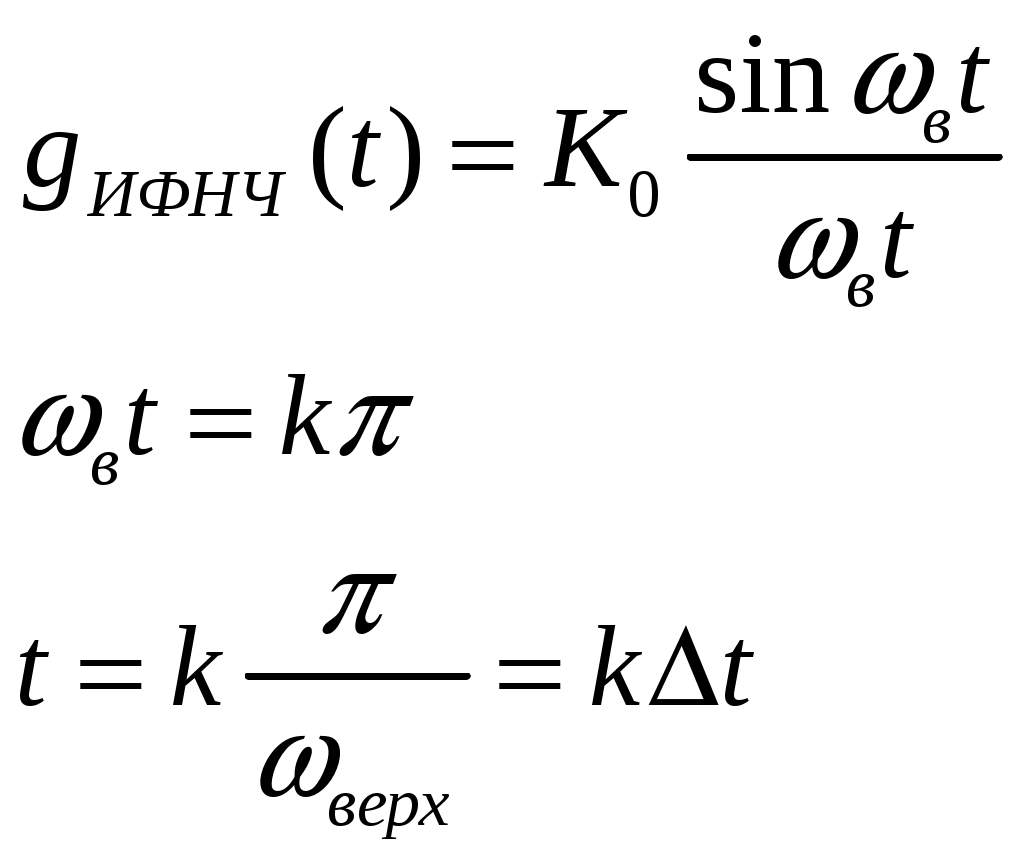

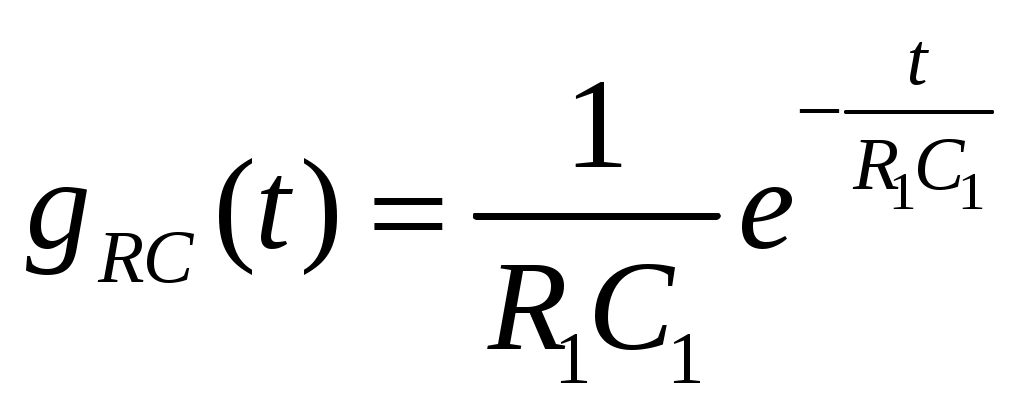 ;
; gRC(t)
gRC(t)