ЛР13. Описание_ЛР_13_01. Лабораторная работа 13 Исследование свойств циклических кодов Москва 2002 План умд 20022003 уч г. Лабораторная работа 13

• Название: Лабораторная работа 13 Исследование свойств циклических кодов Москва 2002 План умд 20022003 уч г. Лабораторная работа 13
• Дата: 15.11.2022
• Размер: 127.5 Kb.
• Имя файла: Описание_ЛР_13_01.doc
• Тип: Лабораторная работа; #790377

Размер 38 строчек * 60символов
Шрифт 14

межстрочный интервал : 1.4

заглавия 16 Bold

поля 2 см

МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ

ПО СВЯЗИ И ИНФОРМАТИЗАЦИИ

Московский технический университет связи и информатики

Кафедра передачи дискретных сообщений и телеграфии



Лабораторная работа №13

Исследование свойств циклических кодов

Москва 2002



План УМД 2002/2003 уч.г.
Лабораторная работа №13

Исследование свойств циклических кодов

Составители: Генкина Нинель Фёдоровна , к.т.н.,

Марков Игорь Александрович.

Рецензент: Яковенко Наталия Викторовна.

Издание утверждено советом факультета АЭСиВТ.
Протокол № 9 от 21.05.02.

1. Цель работы

1. 
   Изучить основные принципы помехоустойчивого кодирования.
   
2. 
   Изучить правила построения циклических кодов.
   
3. 
   Исследовать обнаруживающие и исправляющие свойства циклических кодов.
   

1.4. Познакомиться c принципом построения кодирующих и декодирующих устройств циклических кодов.
2. Индивидуальное задание

В лабораторной работе изучаются свойства циклических кодов на примере разделимого линейного циклического кода (7,4) с образующим полиномом g(x)=X³ + X + 1. Кодовое расстояние этого кода d = 3.

Код может быть использован в режиме исправления ошибок или в режиме обнаружения ошибок.

2.1. Найдите все кодовые слова заданного кода.

2.2. Определите характеристики заданного кода в режиме исправления ошибок:

2.2.1. Определите кратность t гарантированно исправляемых кодом ошибок.

2.2.2. Найдите число различных векторов ошибок, которые код может исправить.

2.2.3. При условии, что кодом в первую очередь исправляются ошибки наименьшей кратности, приведите вектора ошибок, которые могут быть исправлены заданным кодом.

2.2.4. Для одного из векторов ошибок, исправляемых кодом, найдите соответствующий этому вектору синдром. Найдите несколько из возможных векторов ошибок, при декодировании которых получается тот же синдром, и, следовательно, происходит ошибочное декодирование.

2.2.5. При условии, что кодом в первую очередь исправляются ошибки наименьшей кратности, рассчитайте для заданного кода вероятность Pош ошибочного декодирования, если канал является дискретным симметричным каналом без памяти (ДСК) с вероятностью ошибки в двоичном символе p₀.

Численное значение p₀ возьмите из программы лабораторной работы в разделе ‘Индивидуальное задание’.

2.3. Определите возможности заданного кода в режиме обнаружения ошибок:

2.3.1. Определите кратность  гарантированно обнаруживаемых кодом ошибок.

2.3.2. Найдите вектора ошибок, которые не могут быть обнаружены заданным кодом.

2.3.3. Рассчитайте вероятность Pн.о. необнаружения ошибок заданным кодом в ДСК с вероятностью ошибки в символе p₀.
3. Описание программы

Лабораторная работа выполняется на IBM PC совместимом компьютере.

Программное обеспечение лабораторной работы можно записать на кафедре или c сайта кафедры www.pds-01.boom.ru.

Программа содержит несколько страниц:

“Начало” – содержит общие сведения: название работы и.т.п.

Содержит кнопки:

‘о программе’ - можно посмотреть номер версии программы,

адрес сайта МТУСИ и кафедры.

‘переписать’ - активизирует диалоговое окно, используемое для

перезаписи программы, образца отчёта и.т.п. на гибкий диск.

‘выход’ - используется для выхода из программы.

“Установки” - содержит различные установки и панель формирования

индивидуального задания.
*!!!* На распечатках, помещаемых в отчёт должны быть Фамилия И.О. и номер группы исполнителя. Для этого необходимо в начале выполнения работы ввести их в требуемые строки на панели ‘Формирование индивидуального задания’.

“Читайте” - содержит разделы: цель работы, задание, содержание отчёта

и контрольные вопросы. Раздел ‘задание’ содержит лабораторное

задание и методику выполнения каждого пункта.

“Схема ” - содержит схему, иллюстрирующую процесс кодирования и декодирования. На этой странице имеется возможность вводить различные кодовые комбинации, вектора ошибок и наблюдать процесс кодирования и декодирования. Также эта страница содержит таблицу соответствия векторов ошибок и соответствующим им синдромов.

“Таблица” – содержит таблицу разрешённых кодовых комбинаций используемого кода, таблицу расстояний Хемминга для всех пар кодовых комбинаций и таблицу весов кодовых комбинаций.

Имеется возможность изменять образующий полином, используемый для кодирования. Обратите внимание, что только полиномы 1011 и 1101 обеспечивают коду (7,4) требуемые помехоустойчивые свойства (dмин=3).

Выполнять работу рекомендуется при полиноме 1011 (установлен по умолчанию). Это связано с тем, что тестовые вопросы для защиты этой лабораторной работы составлены для полинома 1011.

“Формулы” – содержит некоторые формулы, используемые в лабораторой работе.

“Статистика” – демонстрирует использование различных способов помехоустойчивого кодирования для обнаружения и исправления ошибок.

Для распечатки требуемой страницы необходимо нажать клавишу ‘Печать’ расположенную в левом нижнем углу.

Если распечатка не произойдёт (замечен такой дефект на некоторых типах принтеров), то можно распечатать файл PRINT_13_XX.BMP , который создаётся при каждом нажатии на кнопку ‘Печать’.

Распечатку этого файла можно произвести, например, при помощи редактора Word.

4. Описание функциональной схемы

Функциональная схема лабораторного макета приведена на рис. 1. Информационное слово длиной четыре разряда (k=4) задается нажатием кнопок на панели Источник.

Кодер формирует кодовую комбинацию разделимого циклического кода (7,4) путём добавления к четырём информационным разрядам трёх проверочных разрядов. Проверочные разряды образуются в результате умножения на X³ , и деления получившейся комбинации на образующий полином 1011 ( g(x)=X³+X+1).

Остаток от деления будет представлять проверочные разряды, которые приписываются справа от информационных.

Кодер выдает кодовое слово V длиной n = 7, соответствующее информационному слову M длиной k = 4, поданному на вход кодера.

Семиразрядная кодовая комбинация (вектор V) с выхода кодера подаётся на вход канала. В канале передаваемая кодовая комбинация складывается с семиразрядным вектором ошибки E. Сложение производится поразрядно по модулю 2 (00=0, 01=1, 10=1, 11=0).

Например, если комбинация на входе канала равна 1011000 ,

а вектор ошибки равен 0010001,

то комбинация на выходе канала будет равна 1001001.

Таким образом, единица в i-том разряде в векторе ошибки приводит к ошибке (инверсии) i-того разряда в кодовой комбинации на выходе канала.

Вектор ошибки задаётся на панели Источник ошибок. Там же имеются кнопки для циклического сдвига вектора ошибки и для его инверсии.

С выхода канала принятая кодовая комбинация подаются на входы декодеров.

Декодер 1 работает в режиме исправления ошибок. Если ошибок нет или вектор ошибок принадлежит к векторам ошибок, исправляемых кодом, то сигнал на выходе декодера 1, совпадает с сигналом на входе кодера (выходе источника).

Если сигнал на выходе декодера 1 не совпадает с входным сигналом, поступающим на вход кодера, значит, произошло ошибочное декодирование.

Это соответствует появлению вектора ошибок, который код, используемый в системе, исправить не может. Код (7,4) исправляет все одиночные ошибки.

Исправление одиночной ошибки производится следующим образом:

• 
  принятая 7-ми разрядная комбинация делится на образующий полином;
  
• 
  если остаток от деления (синдром ошибки) не равен нулю, то по таблице соответствия ‘вектор ошибки – синдром’ определяется вектор ошибки, которому соответствует данный синдром;
  
• 
  принятая 7-ми разрядная комбинация складывается по модулю 2 с найденным вектором ошибки.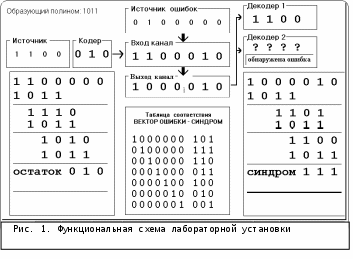
  

Декодер 2 работает в режиме обнаружения ошибок.

Если декодером 2 обнаружена ошибка, то декодер формирует сигнал ‘обнаружена ошибка’ кодовая комбинация при этом не выдаётся (высвечивается ? ? ? ? ). Если вектор ошибок принадлежит к не обнаруживаемым заданным кодом векторам ошибок, сигнал на выходе декодера 2 будет отличным от сигнала, поданного на вход кодера.

Декодер 2 не может обнаружить вектора ошибок, которые совпадают с разрешенными кодовыми комбинациями. Это следует из свойства линейного кода: ‘сумма двух кодовых слов является тоже кодовым словом’.

5. Лабораторное задание

5.1. Проверьте работу кодера.

5.2. Проверьте правильность декодирования при отсутствии ошибок.

5.3. Исследуйте способность кода исправлять ошибки.

5.4. Проверьте факт ошибочного декодирования в режиме исправления ошибок.

5.5. Исследуйте способность кода обнаруживать ошибки.

5.6. Проверьте факт не обнаружения ошибок кодом.

7. 
   Распечатайте таблицу с разрешенными кодовыми комбинациями и таблицу с расстояниями Хемминга для разрешенных комбинаций.
   

6. Методические указания по выполнению работы

6.1 Проверка работы кодера

Задайте в ‘источнике’ различные информационные последовательности.

Пронаблюдайте последовательности, полученные на выходе кодера.

Сравните полученные кодовые слова с результатом индивидуального задания.

6.2 Проверка правильности декодирования при отсутствии ошибок

Установите в ‘датчике ошибок’ все разряды в ноль, т.е. нет ошибок.

Задайте в источнике различные информационные последовательности.

Пронаблюдайте последовательности, полученные на выходе

декодеров (Декодер 1, Декодер 2).

Убедитесь, что при отсутствии ошибок, последовательности на

выходах декодеров совпадают с последовательностью на входе кодера.

При выполнении этого пункта обратите внимание, что при отсутствии ошибок синдром равен нулю.

По результатам этого пункта сделайте распечатку (Распечатка №1).

6.3. Методика исследования способности кода исправлять ошибки

Задайте в 'источнике ошибок' однократную ошибку (например 1000000).

Убедитесь, что на выходе 'Декодера 1' будет та же последовательность,

что и в 'Источнике'.

Сместите циклически 6 раз вектор ошибки и убедитесь, что при любой

однократной ошибке 'Декодер 1' правильно её исправит.

При выполнении этого пункта обратите внимание , что синдром ошибки зависит от вектора ошибки и не зависит от передаваемой комбинации.

По результатам этого пункта сделайте распечатку (Распечатка №2).

6.4. Методика проверки ошибочного декодирования в режиме исправления ошибок.

Задайте в 'Источнике ошибок' несколько векторов ошибок с кратностью от 2 до 7. Убедитесь, что при таких ошибках последовательность на выходе 'Декодера 1' не будет совпадать с последовательностью, которую Вы задали в 'Источнике'.

По результатам этого пункта сделайте распечатку (Распечатка №3).

6.5. Методика исследования способности кода обнаруживать ошибки

Задайте в 'Источнике ошибок' различные ошибки кратностью от 1 до 7.

Убедитесь, что подавляющее большинство векторов ошибок будет обнаружено (на панели 'Декодер 2' будет гореть индикатор 'Обнаружена ошибка').

По результатам этого пункта сделайте распечатку (Распечатка №4).

6.6. Методика проверки факта не обнаружения ошибки кодом

Задайте в 'Источнике ошибок' различные ошибки кратностью от 3 до 7.

Убедитесь, что имеются вектора ошибок, которые кодом не обнаруживаются (при наличии ошибки на панели 'Декодер 2' не будет гореть индикатор 'Обнаружена ошибка').

По результатам этого пункта сделайте распечатку (Распечатка №5).

6.7. Распечатка таблицы с разрешенными кодовыми комбинациями.

Перейдите на закладку 'таблицы' и нажмите клавишу 'Печать'

7. Содержание отчета

Отчёт должен содержать:

стр 1. Титульный лист.

стр 2. Цель работы и функциональную схему лабораторного макета.

!!! Функциональную схему нарисуйте использую карандаш и линейку.

стр 3. Индивидуальное задание.

стр 4. Распечатку №1, показывающую работу кодера и правильности декодирования при отсутствии ошибок.

Распечатку №2, показывающую способности кода исправлять однократную ошибку.

стр 5. Распечатку №3, показывающую факт ошибочного декодирования в режиме исправления ошибок. Распечатку №4, показывающую способности кода обнаруживать ошибки.

стр 6. Распечатку №5, показывающую факт не обнаружения ошибки кодом.

Распечатку №6, показывающую разрешенные кодовые комбинации и

расстояния Хемминга.

стр 7. Краткий ответ на 5 контрольных вопросов (номера вопросов выберите самостоятельно) и выводы по работе.

*** Образец оформления отчёта смотрите в файле: ЛР_13_Образец_отчёта.doc
Список литературы

1. Шварцман В.0., Емельянов Г.А. Теория передачи дискретной информации. - М.: Связь, 1979. - 424 с.

2. 
   Шварцман В.0., Емельянов Г.А. Передача дискретной информации. - М.: Радио и связь, 1982. - 239 с.
   
3. 
   Передача дискретных сообщений. Под редакцией В.П.Шувалова.
   

[с. 49 - 54; с. 245 - 297] –М.:Радио и связь,-1990-464 c.:ил.-

8. Контрольные вопросы

1. Поясните понятия: блочные, непрерывные, разделимые, неразделимые, итеративные, линейные, циклические коды ?

2. Что такое расстояние Хемминга и кодовое расстояние ?

3. Определение и основные свойства циклического кода.

4. Какое правило кодирования циклическим кодом принято в лабораторной работе?

5. Какое правило декодирования принято в декодере в режиме исправления ошибок?

6. Какое правило декодирования принято в декодере в режима обнаружения ошибок?

7. Как связаны кратности гарантированно исправляемых кодом ошибок t и гарантированно обнаруживаемых кодом ошибок  с кодовым расстоянием d ?

8. Какие векторы ошибок не могут быть обнаружены линейным циклическим кодом?

9. Сколько различных векторов ошибок может быть исправлено, не исправлено, обнаружено, не обнаружено кодом (7,4).?

10. Как рассчитать вероятность не обнаружения ошибки при заданном канале?

11. Как рассчитать вероятность ошибочного декодирования при заданном канале?

12. Как по одной известной разрешённой комбинации циклического кода определить все остальные кодовые комбинации этого кода ?

13. Известна комбинация на входе кодера v1 и выходе декодера_2 v2.

Как определить вектор ошибки E ? ( v1<> v2 )

14. Дана длина кодовой комбинации n, вероятность ошибки в канале Pош.

Как определить вероятность появления в кодовой комбинации ошибки

кратностью t ?

15. Как производится кодирование - декодирование при использовании кода с проверкой на чётность (на нечётность) ?

ПРИЛОЖЕНИЕ

КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ЦИКЛИЧЕСКИХ КОДОВ
Линейные коды являются кодами блочными, регулярными. Для регулярных кодов задаются правила преобразования информационного слова длины kв кодовую последовательность длины n (n > k), а также правила декодирования. Наибольшее распространение получили линейные разделимые коды. Разделимым кодом называется код, в кодовых словах которого можно указать места информационных и проверочных символов.

Линейным кодом называют блочный (n, k) код, символы кодовых слов которого являются линейными комбинациями информационных символов.

Если M=(m_k-1,m_k-2,….m₀) обозначает последовательность k двоичных информационных символов, то правило образования кодового слова V разделимого линейного кода с длиной блока n > k из последовательности M можно записать системой линейных уравнений:

(I)



г де - знак суммирования по модулю 2, коэффициенты d_l,i являются символами двоичного алфавита, они могут быть выбраны произвольно, но должны быть фиксированными для данного кода.

Приведем ряд свойств линейных кодов [1, c.283-286] .

1. Сумма по модулю 2 двух кодовых слов также является кодовым словом (свойство замкнутости по отношению к операции сложения).

2. Кодовое расстояние d , определяемое как наименьшее расстояние Хемминга между всеми возможными парами кодовых слов, в линейном коде равно минимальному весу ненулевого кодового слова. (Весом кодового слова называется число содержащихся в нем единиц).

Расстояние Хемминга между двумя кодовыми словами равно числу единиц в сумме этих слов по модулю 2 , т.е. количеству разрядов, в которых различаются эти два кодовых слова. Например:

первое кодовое слово: 1000110,

второе кодовое слово: 0100010,

с умма по модулю два: 1100100 -> расстояние Хемминга равно 3.
Кодовое расстояние d, связано с кратностью t гарантированно исправляемых кодом ошибок соотношением



и с кратностью гарантированно обнаруживаемых кодом ошибок соотношением



Циклические коды относятся к классу линейных кодов и обладают всеми их свойствами. Дополнительным условием по отношению к циклическому линейному коду является условие замкнутости по отношению к операции циклического сдвига кодовых слов.

Циклическим кодом называется такой линейный код, у которого при любом циклическом сдвиге какого-либо кодового слова получается другое кодовое слово.

Циклическим сдвигом называется операция, превращающая вектор V₁= (v₁ ,v₂ ,v₃,…v_n) в вектор V₂= (v_n , v₁ ,v₂ ,…v_n-1) –сдвиг в право, или в вектор V3= (v₂ ,v₃,…v_n ,v₁) – сдвиг влево.

Например, дан вектор 0001011. При циклическом сдвиге

вправо получится вектор 1000101.

Для описания циклических кодов используют математический аппарат, основанный на сопоставлении множества кодовых слов с множеством степенных полиномов . Этот аппарат позволяет выявить для циклического кода более простые операции кодирования и декодирования.

Установим формальное соответствие между кодовыми словами и степенными полиномами. Кодовому слову

V= (v_n-1 , v_n-2 , v_n-3 ,…v₁ , v₀)

где v_n-1 , v_n-2 , v_n-3 ,…v₁ , v₀ двоичные числа, можно поставить в соответствие полином (n-1)-й степени

V(x) = v_n-1 x^n-1 + v_n-2 x^n-1 + …+ v₁ x + v₀.

Такая запись соответствует записи числа в виде многочлена в двоичной системе счисления, где x - основание системы счисле­ния.

Например, кодовому слову 0001011 соответствует полином

x³ + x + 1, кодовому слову 0100110 – полином x⁵ + x² +x.

Операцию сложения кодовых слов можно заменить сложением соответствующих полиномов. Например, сложив по модулю 2 полиномы из вышеприведенного примера, получим:

( ) ( ) = ( ).

Этому полиному соответствует слово 0101101, т.е. результат поразрядного сложения по модулю 2 слов 0001011 и 0100110.

Умножение полинома v(x) на x по модулю (xⁿ 1) соответствует циклическому сдвигу кодового слова влево на один разряд.

Числом А по модулю В называется остаток от деления А на В и обозначается A mod B.

В вашем случае все полиномы степени выше (n-1) заменяются остатком от их деления на полином xⁿ 1.

Среди всех полиномов, соответствующих кодовым словам циклического кода, имеется ненулевой полином g(x) наименьшей степени. Этот полином полностью определяет соответствующий код и поэтому называется образующим [l, с. 297-293].

Степень образующего полинома g(x) равна n-k, свободный член всегда равен единице.

Образующий полином является делителем всех полиномов, соот­ветствующих кодовым словам циклического кода.

Нулевая комбинация обязательно принадлежит любому линейному циклическому коду и может быть записана как (xⁿ 1) mod (xⁿ 1) = 0 . Следовательно, образующий полином g(x) должен быть делителем бинома xⁿ 1.

Это даёт конструктивную возможности построения циклического кода заданной длины n: любой полином, являющийся делителем бинома xⁿ 1, можно использовать в качестве образующего.

При построении циклических кодов, пользуются таблицами разложения биномов xⁿ 1 на неприводимые полиномы, т.е. полиномы, которые нельзя представить в виде произведения двух других полиномов.

Любой неприводимый полином, входящий в разложение бинома xⁿ 1, а также любое произведение неприводимых полиномов может быть выбрано в качестве образующего полинома, что дает соответствующий циклический код.

Для построения разделимого циклического кода используется следующее правило построения кодовых слов [1, с. 300] [2, с. 110-113]

V(x) = m(x)*x^n-k  r(x),

где r(x) - остаток от деления m(x)*x^n-k на g(x).

Степень r(x), очевидно, меньше (n-k), а потому в кодовом слове первые k, символов будут совпадать с информационными, а последние n - k символов будут проверочными.

Получить все разрешённые комбинации циклического кода можно по одной известной кодовой комбинации (не нулевой). Для этого сначала надо циклически сдвинуть известную комбинацию k-1 раз. В результате получится n комбинаций. Затем сложить попарно по модулю 2 получившиеся комбинации в различных сочитаниях (по две, по три и.т.д). Нулевую комбинацию (все нули) можно получить, сложив по модулю 2 любую комбинацию саму с собой. Всего получится 2^k кодовых слов.

В основу процедуры декодирования циклических кодов может быть положено свойство их делимости без остатка на образующий полином g(x).

В режиме обнаружения ошибок, если принятая последовательность делится без остатка на g(x), делается вывод, что ошибки нет или она не обнаруживается. В противном случае комбинация бракуется.

Слова любого линейного кода обладают свойством замкнутости по отношению к операции сложения, т.е. сумма двух и более кодовых слов тоже является кодовым словом.

Из этого свойства, видно, что векторы ошибок, совпадающие с кодовыми словами, не могут быть обнаружены декодером циклического кода.

Вектором ошибок называется двоичная последовательность длины n , в которой единицы стоят на позициях ошибочных символов. Отсюда вероятность не обнаружения ошибки заданным кодом равна вероятности появления в заданном дискретном канале векторов ошибок, совпадающих с кодовыми словами.

Относительно просто эти вероятности могут быть рассчитаны для двоичного симметричного канала (ДСК) без памяти.

В таком канале каждый двоичный символ с некоторой фиксированной вероятностью (1 - p₀) принимается правильно и с вероятностью p₀ изменяется помехой на обратный. Передача - приём каждого символа полагается событием независимым (канал без памяти).

Если по такому каналу передается кодовое слово длины n , то вероятность P_n(0) того, что не произойдет ни одной ошибки, равна (1- p₀)ⁿ.

Вероятность P_n(1) того, что будет одна ошибка в заданном символе, равна p₀*(1- p₀)^n-1.

Вероятность того, что слово на выходе канала будет отличаться от переданного слова в заданных t разрядах, т.е. вектор, ошибок содержит t единиц, равна P^*=p₀^t (1 - p₀) ^n-t.

В
t


t

ероятность того, что слово на выходе канала будет отличаться от переданного слова в любых t разрядах, равна

P_n (t) = C_n p₀^t (1 - p₀) ^n-t. , где С_n – число сочетаний из n по t .

Число единиц в векторе ошибок часто называют его весом.

Положим некоторый линейный код (5,3) содержит одно нулевое слово (как всякий линейный код), два слова веса 2, четыре слова веса 3, одно слово веса 4 (всего слов).

Вероятность не обнаруживаемой ошибки этим кодом равна вероятности появления в ДСК векторов ошибок, совпадающих с кодовыми словами, т.е.:



В режиме исправления ошибок декодер вычисляет остаток S(x) от деления принятой последовательности P(x) на g(x). Этот остаток называют синдромом. Принятый полином P(x) представляет собой сумму по модулю два переданного слова V(x) и вектора ошибок E(x):

P(x) = V(x) E(x)

Тогда синдром S(x)= P(x) mod g(x), так как по определению циклического кода V(x)mod g(x) =0.

Оопределенному синдрому S(x) может быть поставлен в соответствие определенный вектор ошибок E(x). Тогда переданное слово V(x) находят, складывая P(x)E(x).

Однако один и тот же синдром может соответствовать 2^k различным векторам ошибок. Положим, синдром S(x) соответствует вектору ошибок E₁(x). Но и все векторы ошибок, равные сумме E₁(x) V(x), где V(x) любое кодовое слово, будут давать тот же синдром. Поэтому, поставив в соответствие синдрому S1(x) вектор ошибок E₁(x), мы будем осуществлять правильное декодирование в случае, когда действительно вектор ошибок равен E₁(x), во всех остальных 2^k-1 случаях декодирование будет ошибочным.

Для уменьшения вероятности ошибочного декодирования из всех возможных векторов ошибок, дающих один и тот же синдром, следует выбирать в качестве исправляемого наиболее вероятный в заданном канале.

Например, в ДСК, в котором вероятность p₀ ошибочного приёма двоичного символа много меньше вероятности (1 - p₀) правильного приема, вероятность появления векторов ошибок уменьшается с увеличением их веса t . В этом случае следует исправлять в первую очередь вектор ошибок меньшего веса.

Если кодом могут быть исправлены только все векторы ошибок веса t и меньше, то любой вектор ошибки веса от t + 1до n, будет приводить к ошибочному декодированию.

Вероятность ошибочного декодирования будет равна вероятности P_n(>t) появления векторов ошибок веса t + 1 и больше в заданном канале. Для ДСК эта вероятность будет равна


i i
.

Общее число различных векторов ошибок, которые может исправлять циклический код, равно числу ненулевых синдромов – 2^n-k - 1.

18