моделирование оптических систем. Гайнетдинова Лабораторные работы. Лабораторная работа 13 моделирование оптических систем цель работы
 Скачать 117.58 Kb. Скачать 117.58 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №13 МОДЕЛИРОВАНИЕ ОПТИЧЕСКИХ СИСТЕМ ЦЕЛЬ РАБОТЫ: Ознакомление с оптическими схемами зрительной трубы Кеплера и микроскопа. Моделирование этих схем из простых линз. Проверка формул увеличения зрительной трубы Кеплера и микроскопа. ЭКСПЕРИМЕНТ 1. Зрительная труба Кеплера Ход работы: 1.Подведили маркер мыши к движку регулятора F1, нажали левую кнопку мыши и, удерживая её в нажатом состоянии, двигали движок до установки значения F1, взятого из таблицы 1 для нашей бригады. 2. Установили аналогичным образом F2 и . 3. Записали в таблицу 2 значение Гт 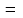  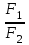 , взятое из нижнего правого окна схемы зрительной трубы Кеплера. , взятое из нижнего правого окна схемы зрительной трубы Кеплера.4. С помощью миллиметровой линейки измерили на экране монитора D и D и записали эти значения в таблицу 2. 5. Рассчитали значение Гэ = 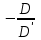 и записали это значение в таблицу 2. и записали это значение в таблицу 2.6. Сравнили полученное значение Гэ со значением Гт. 7. Устанавливая вторые значения F1 и F2, взятые из таблицы 1 для нашей бригады, повторили измерения по п. 2-6, записывая результаты измерений в табл. 2. 8. Оценили абсолютную погрешность измерений. Формулы для расчета: Г = 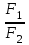 , , Г = 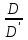 . .ТАБЛИЦА 1.
ТАБЛИЦА 2.
ЭКСПЕРИМЕНТ 2. Микроскоп. 1.Подведили маркер мыши к движку регулятора фокусного расстояния объектива микроскопа, нажали левую кнопку мыши и, удерживали её в нажатом состоянии, перемещая движок до установки F1, взятого из таблицы 1 для нашей бригады. 2.Установили аналогичным образом фокусное расстояние окуляра F2 и записали эти значения в табл. 2. 4. С помощью миллиметровой линейки измерили расстояния d1, d2, f1, f2 и записали их в таблицу 2. 5. По формулам рассчитали kоб, kок и Г и записали эти значения в табл. 2. 4.Рассчитали по формуле теоретическое значение оптического интервала т по параметрам, указанным в нижней части окна. 6.Определили масштаб шкалы окна оптической схемы микроскопа. Для этого измерили с помощью миллиметровой линейки на экране монитора фокусное расстояние F1 и сопоставили его со значением, указанным в левом нижнем прямоугольнике окна оптической схемы. 7.Измерили с помощью миллиметровой линейки на экране монитора оптический интервал микроскопа, привели его в соответствие с масштабом шкалы окна и записали полученное значение интервала в табл. 2 (графа э). 8.Сопоставили полученные экспериментальные значения оптического интервала и увеличения микроскопа с указанными в окошке опыта значениями и сделали анализ опыта. 9. Сделали оценку погрешности измерений. Формулы для расчета: Увеличение изображения, даваемое объективом:  Увеличение изображения, даваемое окуляром: 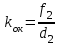 . .Увеличение микроскопа выражается формулой: 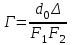 . .ТАБЛИЦА 1.
ТАБЛИЦА 2.
kоб=38/15=2,53 kок=78/11=7,09 Г=2,53х7,09=17,93 Δт =ГхF1F2/d0=18,8х35х40/250=105,28 Вывод: Увеличение микроскопа тем выше, чем короче фокусное расстояние объектива и окуляра (при условии, что фокусное расстояние окуляра больше фокусного расстояния объектива). Погрешности в определении оптического интервала объясняются неточностью снятия размеров с экрана монитора. Вопросы и задания для самоконтроля Линза – прозрачное тело, ограниченное криволинейными поверхностями. Оптический центр линзы – это точка, проходя через которую лучи не меняют своего направления. Главная оптическая ось – прямая, проходящая через центры сферических поверхностей линзы. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой. Главная оптическая ось – прямая, проходящая через центры сферических поверхностей линзы. Побочная оптическая ось – любая прямая, кроме главной оптической оси, проходящая через оптический центр. Если на собирающую линзу пустить пучок света параллельно главной оптической оси, то после прохождения лучей через линзу они пересекутся в одной точке F, которая называется фокусом линзы. Чтобы построить изображение точки, нужно взять луч и направить его произвольно на линзу. При помощи рассеивающей линзы невозможно получить действительное изображение. Изображение, даваемое рассеивающей линзой, является мнимым, прямым и уменьшенным, и не зависит от взаиморасположения линзы и предмета. Лучи, идущие параллельно главной оптической оси собирающей линзы, после неё «сходятся», проходя через точку F – действительный главный фокус собирающей линзы. Постулат в геометрической оптике, согласно которому свет выбирает из множества путей между двумя точками тот путь, который потребует наименьшего времени. Оптическая сила — величина, характеризующая преломляющую способность осемметричных линз и центрированных оптических систем из таких линз. Измеряется в диоптриях (обозначение: дптр): 1 дптр=1 м−1. Сферическая аберрация Кома Хроматическая аберрация Ахроматическая линза 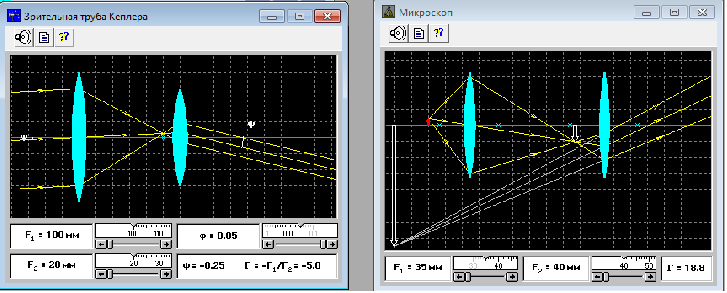 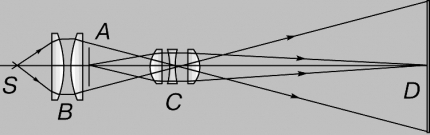 Телескопическая оптическая система — оптическая система (фокусное расстояние которой неограниченно большое), преобразующая параллельный световой пучок в параллельный же, но с другим углом наклона оптической оси.
ЛАБОРАТОРНАЯ РАБОТА № 4 ОПРЕДЕЛЕНИЕ ПЕРИОДА КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ МЕТОДОМ ДИФРАКЦИИ ЭЛЕКТРОНОВ ЦЕЛЬ РАБОТЫ: Изучение волновых свойств электронов. Знакомство с компьютерной моделью дифракции электронов при их рассеянии на одномерной монокристаллической решётке (электронография). Определение периода кристаллической решётки «плёнки металла». ОБОРУДОВАНИЕ: Схема динамической модели для определения периода кристаллической решетки методом дифракции электронов. Ход работы: 1. Нажали мышью кнопку «Выбор» и, зацепив мышью движок регулятора периода решётки, установили значение d = 1,51010 м. 2. Аналогичным образом установили первое значение скорости электронов, указанное в табл.1 для нашей бригады. 3. Нажали мышью кнопку «Старт» и наблюдайте движение электронов через одномерную модель дифракционной кристаллической решётки и их регистрацию на фотопластинке. 4. Определили по шкале, расположенной в правой части окна, координаты первых трёх максимумов интенсивности дифракционной картины и записали эти значения в таблицу 2. 5. Установили второе значение скорости для нашей бригады и повторили эти измерения ещё раз. Формулы для расчета: 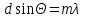 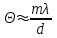 ; ; ; ;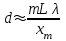 Таблица 1. Значения скорости электронов
Таблица 2. Результаты измерений и расчётов
Для V1= 1,5*107, м/с 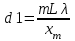 =1*0,1*0,49*10-10/3*10-2=0,016*10-8м=1,6*10-10м =1*0,1*0,49*10-10/3*10-2=0,016*10-8м=1,6*10-10м 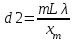 =2*0,1*0,49*10-10/6,5*10-2=1,5*10-10м =2*0,1*0,49*10-10/6,5*10-2=1,5*10-10м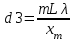 =3*0,1*0,49*10-10/9*10-2=1,6*10-10м =3*0,1*0,49*10-10/9*10-2=1,6*10-10мdэ сред=(1,6+1,5+1,6)/3=4,7/3=1,56 Погрешность :1,56-1,5=0,06=>0,06/1,5*100%=4% Для V2= 2*107, м/с 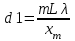 =1*0,1*0,37*10-10/2,5*10-2=1,48*10-10м =1*0,1*0,37*10-10/2,5*10-2=1,48*10-10м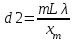 =2*0,1*0,37*10-10/4,8*10-2=1,54*10-10м =2*0,1*0,37*10-10/4,8*10-2=1,54*10-10м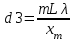 =3*0,1*0,37*10-10/6,7*10-2=1,65*10-10м =3*0,1*0,37*10-10/6,7*10-2=1,65*10-10мdэ сред=(1,65+1,54+1,48)/3=1,55 Погрешность:1,55-1,5=0,05=>0,05/1,5*100%=3% Вывод: В ходе изучения волновых свойств электронов был определен период кристаллической решётки плёнки металла и определена относительная погрешность, равная 4% при первом измерении и 3% во втором. Вопросы и задания для самоконтроля Отличие аморфных и кристаллических веществ заключается в степени упорядоченности их внутреннего строения. В кристаллических веществах все частицы располагаются в определённом порядке. В аморфных веществах этот порядок относительный. Вспомогательный геометрический образ, вводимый для анализа строения кристалла Точки, в которых размещены частицы, называются узлами кристаллической решетки. Монокристалл — отдельный кристалл, имеющий непрерывную кристаллическую решётку (в противоположность поликристаллу — телу из сросшихся кристаллов). В зависимости от природы частиц, помещающихся в узлах кристаллической решетки, и от характера сил взаимодействия между ними различаются четыре типа кристаллических решеток (четыре типа кристаллов): ионные, атомные, металлические и молекулярные. Сильная химическая связь, возникающая в результате электростатического притяжения катионов и анионов. Возникает между атомами с большой разностью электроотрицательностей, при которой общая электронная пара переходит преимущественно к атому с большей электроотрицательностью. Химическая связь, образованная перекрытием пары валентных электронных облаков. Обеспечивающие связь электронные облака называются общей электронной парой. Низшая категория (все трансляции не равны друг другу) Триклинная {\displaystyle a\neq b\neq c} {\displaystyle \alpha \neq \beta \neq \gamma \neq 90^{\circ }} Моноклинная {\displaystyle a\neq b\neq c} {\displaystyle \alpha =\gamma =90^{\circ },\beta \neq 90^{\circ }} Ромбическая {\displaystyle a\neq b\neq c} {\displaystyle \alpha =\beta =\gamma =90^{\circ }} Средняя категория Тетрагональная {\displaystyle a=b\neq c} {\displaystyle \alpha =\beta =\gamma =90^{\circ }} Гексагональная {\displaystyle a=b\neq c} {\displaystyle \alpha =\beta =90^{\circ },\gamma =120^{\circ }} Ромбоэдрическая {\displaystyle a=b=c} {\displaystyle \alpha =\beta =\gamma <120^{\circ }\neq 90^{\circ }} Высшая категория (все трансляции равны между собой) Кубическая {\displaystyle a=b=c}Идея волн де Бройля полезна для приблизительных выводов о масштабах проявления волновых свойств частиц, но не отражает всей физической реальности и потому не лежит в основе математического аппарата квантовой механики. Вместо дебройлевских волн эту роль в квантовой механике выполняет волновая функция, а в квантовой теории поля — полевые операторы. {\displaystyle \alpha =\beta =\gamma =90^{\circ }} Соотношение неопределенностей является математическим выражением принципа неопределенностей. Согласно этому принципу в природе не существует состояния частицы с точно определенными значениями координаты и проекции импульса на эту координатную ось. Комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Квадрат модуля волновой функции определяет плотность вероятности нахождения частицы (электрона): dw/dV = |Ψ|2. 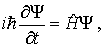 Дифракция частиц – рассеяние микрочастиц (электронов, нейтронов, атомов и т. п.) кристаллами или молекулами жидкостей и газов, при котором из начального пучка частиц данного типа возникают дополнительно отклонённые пучки этих частиц. Большой интерес представляет также дифракция на пространственных (трехмерных) решетках — пространственных образованиях, в которых элементы структуры подобны по форме, имеют геометрически правильное и периодически повторяющееся расположение, а также постоянные (периоды) решеток, соизмеримые с длиной волны электромагнитного излучения. Иными словами, подобные пространственные образования должны иметь периодичность по трем не лежащим в одной плоскости направлениям. В качестве пространственных дифракционных решеток могут быть использованы кристаллические тела, так как в них неоднородности (атомы, молекулы, ионы) регулярно повторяются в трех направлениях. Условие Вульфа-Брэгга определяет направление максимумов дифракции упруго рассеянного на кристалле рентгеновского излучения. Выведено в 1913 независимо У. Л. Брэггом и Г. В. Вульфом. Имеет вид: где d — межплоскостное расстояние, θ — дифракционный угол , n — порядок отражения, λ — длина волны. 1927 г. Дэвиссон и Джермер открыли явление дифракции электронов. ЭЛЕКТРОНОГРАФИЯ- метод изучения структуры в-ва, основанный на исследовании рассеяния образцом ускоренных эл-нов. Применяется для изучения ат. структуры кристаллов, аморфных тел и жидкостей, молекул газов и паров. Дифракция электронов была открыта в 1927 г. и в настоящее время достаточно широко применяется при исследовании металлов и сплавов. Рассмотрим основные особенности этого метода. 1.Взаимодействие электронов с веществом на несколько порядков превосходит взаимодействие рентг. лучей и нейтронов. Поэтому при съемке на просвет можно исследовать очень тонкие объекты (10 -5 — 10 -7 см). При съемке на отражение глубина проникновения составляет 30-200 А, поэтому электронографическими методами возможно исследование очень тонких пленок на поверхности металла (например оксидных). 2. Особенности рассеяние электронов позволяют значительно проще, чем в нейтронографии, определять структурные положения легких атомов в присутствии более тяжелых. Изучение дифракции электронов проводят в специальном приборе называемом электронографом. Электронограф имеет осветительную систему, которая состоит из электронной пушки, являющейся источником электронов, и двух электромагнитных линз. Исследуемый объект помещается в одной из двух камер. Образцы закрепляются в специальном держателе, который позволяет изменять ориентацию образца по отношению к первичному пучку электронов. Для наблюдения за дифракционной картиной предназначен специальный экран, так же возможна фоторегистрация дифракц. картины. Принцип действия электронографа следующий. Электроны, поступая с катода, ускоряются электрическим полем по направлению к заземленному аноду, имеющему отверстие, пройдя через которое, попадают в поле электромагнитных линз. Фокусировка электронов производится двумя конденсорными линзами. Фокус второй линзы лежит в плоскости фотографической пластинки. Электроны прошедшие через образец, дают дифракционную картину на той же фотопластинке. Изображение можно получать либо с одной второй линзой либо с двумя (рис.), в последнем случае достигается максимальная разрешающая способность. Современные электронные микроскопы также позволяют получать электронограммы от малого (0,5-2 мкм 2 ) участка тонкого образца, т.е. осуществлять так называемую микродифракцию. Применяются два типа съемки: на просвет и на отражение (рис.). Монокристаллические образцы дают точечные электронограммы, поликристаллические — в виде концентрических колец. Четкость и интенсивность линий в методе отражения, заметно меньше, чем при съемке на просвет. Для электронографического исследования методом на просвет необходимо применять образец толщиной не более 2 . 10 -6 см. Лишь из небольшого числа веществ возможно приготовить пленки такой толщины. Часто применяют специальную подложку из целлулоидной пленки толщиной около 10 -7 см. Для нанесения исследуемого вещества применяют кристаллизацию из раствора, осаждение из пара или аэрозолей. Образцами для съемки на отражение могут служить металлографические шлифы, размером 10х10 мм. Для снятия жировых и окисных пленок применяют электролитическую полировку. Рассмотрим расчет электронограмм. Длина волны l, связанная с движением электронов, ускоренных разностью потенциалов U (В), определяется (без учета релятивистской поправки) соотношением l = 12,236 . U -1/2 , откуда следует, что при ускоряющем напряжении 40-60 кВ длины волн электронов меняются от 0,037 до 0,062 А и поэтому брегговские углы также будут малы порядка 3-6 о . Можно считать, что sin(q)= q = tg(q). Тогда где r — радиус интерференционного кольца на электронограмме от поликристаллического образца; L — расстояние от образца до фотопластинки. Отсюда где D — диаметр интерференционного кольца. Данной формулой пользоваться трудно, поскольку непосредственное определение l и L недостаточно точно. На практике определяют так называемую постоянную электронографа C=L×l, снимая эталонный образец с известными межпластиночными расстояниями dhkl. Расчет проводят по формуле Точность определения межплоскостных расстояний по электронограмам невелика, что связано с малостью брегговских углов. Рассмотрим применение дифракции электронов для исследования твердых веществ. Структурная электронография. Метод включает в себя методику определения параметров элементарной ячейки и расшифровку атомной структуры из распределения интенсивности рассеянного излучения в обратном пространстве. Методом структурной электронографии исследовано большое число соединений, расшифрованы структуры веществ, содержащих атомы легких элементов, например структура парафинов. Электронографию применяют так же для исследования веществ, неустойчивых в обычных условиях, но устойчивых в вакууме. Электронография поверхностных слоев. Поскольку при съемке на отражение глубина проникновения электронов не превышает 30-200 А, это метод используется для изучения процессов протекающих в тонких поверхностных слоях (окисление, коррозия и т.п.), а так же влияния давления, ковки, шлифовки и т.д. на эти слои. Субмикроскопическая кристаллография. В природе встречаются вещества известные только в мелкодисперсном состоянии, например сажи, различные абразивы, глинистые материалы. Их невозможно исследовать рентгенографически, но в тоже время они дают вполне удовлетворительные электронограммы. В современных электронных микроскопах имеется возможность получения электронограмм от интересующей точки объекта. Таким образом удается получить информацию как о форме дисперсной частицы, так и о ее структуре. Электронографию можно использовать так же для изучения структуры аморфных тел и жидкостей, для изучения строения молекул в парах и газах. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
