практическая работа КодИС. Лабораторная работа 13. Разработка приложений для моделирования процессов и явлений. Отладка приложения

• Название: Лабораторная работа 13. Разработка приложений для моделирования процессов и явлений. Отладка приложения
• Анкор: практическая работа КодИС
• Дата: 30.01.2023
• Размер: 38.56 Kb.
• Имя файла: 12.docx
• Тип: Лабораторная работа; #911906

ЛАБОРАТОРНАЯ РАБОТА № 13. РАЗРАБОТКА ПРИЛОЖЕНИЙ ДЛЯ МОДЕЛИРОВАНИЯ ПРОЦЕССОВ И ЯВЛЕНИЙ. ОТЛАДКА ПРИЛОЖЕНИЯ

Цель: получение навыков разработки и отладки приложений для моделирования процессов и явлений.

Теоретические вопросы

Понятие модели.

Моделирование процессов и явлений.

Технологии моделирования процессов и явлений в приложениях.

Задание № 1. Разработать физико-математическую модель системы при сободном падении физического тела, брошенного с высоты h и падающего свободно в течение t времени. При построении модели принять следующие гипотезы:

1. 
   падение происходит в вакууме (то есть коэффициент сопротивления воздуха равен нулю);
   
2. 
   ветра нет;
   
3. 
   масса тела неизменна;
   
4. 
   тело движется с одинаковым постоянным ускорением g в любой точке.
   

Слово "модель" (лат. modelium) означает "мера", "способ", "сходство с какой-то вещью".

Проблема моделирования состоит из трех взаимосвязанных задач: построение новой (адаптация известной) модели; исследование модели (разработка метода исследования или адаптация, применение известного); использование (на практике или теоретически) модели.

Схема построения модели М системы S с входными сигналами X и выходными сигналами Y изображена на рисунке 28.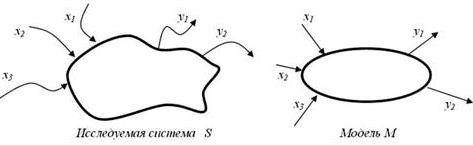



Рисунок 28
Если на вход М поступают сигналы из X и на входе появляются сигналы из Y, то задан закон, правило f функционирования модели, системы.

Классификацию моделей проводят по различным критериям.

Модель – статическая, если среди параметров описания модели нет (явно) временного параметра.

Модель – динамическая, если среди параметров модели явно выделен временной параметр.

Модель – дискретная, если описывает поведение оригинала лишь дискретно, например, в дискретные моменты времени (для динамической модели).

Модель – непрерывная, если описывает поведение оригинала на всем промежутке времени.

Модель – детерминированная, если для каждой допустимой совокупности входных параметров она позволяет определять однозначно набор выходных параметров; в противном случае – модель недетерминированная, стохастическая (вероятностная).

Модель – функциональная, если представима системой функциональных соотношений (например, уравнений).

Модель – теоретико-множественная, если представима некоторыми множествами и отношениями их и их элементов.

Модель – логическая, если представима предикатами, логическими функциями и отношениями.

Модель – информационно-логическая, если она представима информацией о составных элементах, подмоделях, а также логическими отношениями между ними.

Модель – игровая, если она описывает, реализует некоторую игровую ситуацию между элементами (объектами и субъектами игры).

Модель – алгоритмическая, если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим ее функционирование, развитие. Введение такого, на первый взгляд, непривычного типа моделей (действительно, кажется, что любая модель может быть представлена алгоритмом ее исследования), на наш взгляд, вполне обосновано, так как не все модели могут быть исследованы или реализованы алгоритмически.

Модель – графовая, если она представима графом (отношениями вершин и соединяющих их ребер) или графами и отношениями между ними.

Модель – иерархическая (древовидная), если она представима иерахической структурой (деревом).

Модель – языковая, лингвистическая, если она представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой. Иногда такие модели называют вербальными, синтаксическими и т.п.

Модель – визуальная, если она позволяет визуализировать отношения и связи моделируемой системы, особенно в динамике.

Модель – натурная, если она есть материальная копия оригинала.

Модель – геометрическая, если она представима геометрическими образами и отношениями между ними.

Модель – имитационная, если она построена для испытания или изучения, проигрывания возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.

Задание № 2. Разработать статическая модель движения тела по наклонной плоскости F = am. Динамическая модель типа закона Ньютона: F(t) = a(t)m(t) или, еще более точно и лучше, F(t)=s''(t)m(t). Если рассматривать только t = 0.1, 0.2, …, 1 (с), то модель St = gt2/2 или числовая последовательность S0 = 0, S1 = 0.01g/2, S2 = 0.04g, …, S10 = g/2 может служить дискретной моделью движения свободно падающего тела. Модель S = gt2/2, 0 < t < 10 непрерывна на промежутке времени (0;10).

Задание № 3. Разработать модель популяции рыб, из которой в текущий момент времени изымается некоторое количество особей (идет лов рыбы). Динамика такой системы определяется моделью вида: xi + 1 = xi + аxi – kxi, х0 = c , где k – коэффициент вылова (скорость изъятия особей). Стоимость одной пойманной рыбы равна b руб. Цель моделирования – прогноз прибыли при заданной квоте вылова. Для этой модели можно проводить имитационные вычислительные эксперименты и далее модифицировать модель, например следующим образом.

Эксперимент 1. Для заданных параметров a, c изменяя параметр k, определить его наибольшее значение, при котором популяция не вымирает.

Эксперимент 2. Для заданных параметров c, k изменяя параметр a, определить его наибольшее значение, при котором популяция вымирает.

Модификация 1. Учитываем естественную гибель популяции (за счет нехватки пищи, например) с коэффициентом смертности, равным, b: xi + 1 = xi + аxi – (k + b)xi, х0 = c .

Модификация 2. Учитываем зависимость коэффициента k о от x (например, k = dx):
.