Лабораторная работа 2 Дисциплина Программирование нейронных сетей
 Скачать 155.28 Kb. Скачать 155.28 Kb.
|
|
федеральное государственное бюджетное образовательное учреждение высшего образования «Вологодский государственный университет» Институт математики, естественных и компьютерных наук (наименование института) Кафедра «Автоматики и вычислительной техники» (наименование кафедры) ЛАБОРАТОРНАЯ РАБОТА № 2
Вологда 2023 г. Лабораторная работа № 2. Часть 1 Персептроны и однослойные персептронные нейронные сети Цель работы: изучение модели нейрона персептрона и архитектуры персептронной однослойной нейронной сети; создание и исследование моделей персептронных нейронных сетей в системе MATLAB Порядок выполнения работы
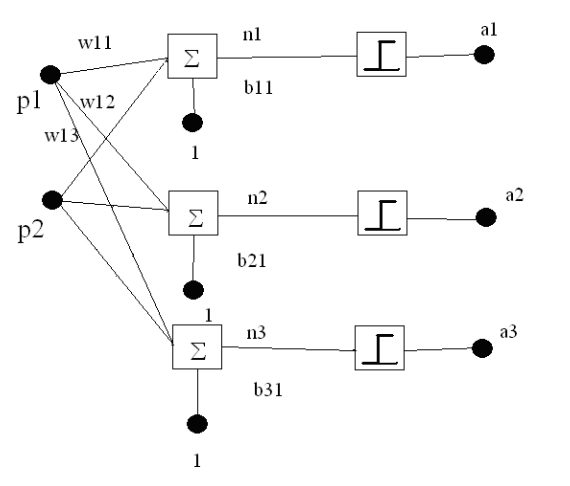 Рисунок 1. Структурная схема персептронной нейронной сети Моделирование персептронной нейронной сети Для формирования однослойного персептрона в системе MATLAB предназначена функция newp net=newp(PR, S) В формуле входными аргументами выступают: PR – массив диапазона значений вектора входа; S – число нейронов в слое. По умолчанию веса и смещения равны нулю, поэтому необходимо установить значения весов w и смещение b. В данном задании элементы вектора входа передаются в сеть через матрицу весов W, имеющую вид: Каждый нейрон имеет смещение b, которое суммируется с значениями входов с учетом их веса. Результирующая сумма n для каждого нейрона равна n1=w11*p1+w12*p2+b1 n2=w21*p1+w22*p2+b2 Эта сумма преобразуется функцией активации f, на выходе которой получаем выход нейрона а. Выходы слоя нейронов формируют вектор-столбец. Уравнение однослойного персептрона имеет вид a = f (Wp + b) где W – матрица весов, p – вектор входов, b – вектор смещения. Для реализации модели персептронной нейронной сети используем систему MATLAB. Код программы: % cоздание персептрона с диапазоном значений входов [-7..7] и 3 нейронами net = newp([-7 7;-7 7],3); % указание начальных значений весов net.IW{1,1,1} = [-1, 0; 2, -2; 4, -5]; %присваивание переменной wts значений весов wts=net.IW{1,1,1}; % указание начальных значений смещения net.b{1} = [2;-1;3]; %присваивание переменной bias значений смещений bias = net.b{1}; % указание диапазона значений входа р1 для построения ограничивающих линий p1 = [-7; 7]; % расчет значений входа р2 для построения первой линии p2=(wts(1,1)*p1-bias(1))/wts(1,2); plot(p1,p2,'r') % расчет значений входа р3 для построения второй линии p3=(wts(2,1)*p1-bias(2))/wts(2,2) % расчет значений входа р4 для построения третей линии p4=(wts(3,1)*p1-bias(3))/wts(3,2) hold on plot(p1,p2,p1,p3,p1,p4); p3 = 6.5000 -7.5000 p4 = 6.2000 -5.0000 %задание функции инициализации для весов и смещения >> net.inputweights{1,1,1}.initFcn = 'rands'; net.biases{1}.initFcn = 'rands' net = Neural Network name: 'Custom Neural Network' userdata: (your custom info) dimensions: numInputs: 1 numLayers: 1 numOutputs: 1 numInputDelays: 0 numLayerDelays: 0 numFeedbackDelays: 0 numWeightElements: 9 sampleTime: 1 connections: biasConnect: true inputConnect: true layerConnect: false outputConnect: true subobjects: input: Equivalent to inputs{1} output: Equivalent to outputs{1} inputs: {1x1 cell array of 1 input} layers: {1x1 cell array of 1 layer} outputs: {1x1 cell array of 1 output} biases: {1x1 cell array of 1 bias} inputWeights: {1x1 cell array of 1 weight} layerWeights: {1x1 cell array of 0 weights} functions: adaptFcn: 'adaptwb' adaptParam: (none) derivFcn: 'defaultderiv' divideFcn: (none) divideParam: (none) divideMode: 'sample' initFcn: 'initlay' performFcn: 'mae' performParam: .regularization, .normalization plotFcns: {'plotperform', 'plottrainstate'} plotParams: {1x2 cell array of 2 params} trainFcn: 'trainc' trainParam: .showWindow, .showCommandLine, .show, .epochs, .time, .goal, .max_fail weight and bias values: IW: {1x1 cell} containing 1 input weight matrix LW: {1x1 cell} containing 0 layer weight matrices b: {1x1 cell} containing 1 bias vector methods: adapt: Learn while in continuous use configure: Configure inputs & outputs gensim: Generate Simulink model init: Initialize weights & biases perform: Calculate performance sim: Evaluate network outputs given inputs train: Train network with examples view: View diagram unconfigure: Unconfigure inputs & outputs evaluate: outputs = net(inputs) >> net = init(net); >> wts = net.IW{1,1,1}, bias = net.b{1}; wts = 0.4121 -0.9077 -0.9363 -0.8057 -0.4462 0.6469 >> bias = net.b{1} bias = -0.2155 0.3110 -0.6576 >> % проверка приналежности входного значения к классу 1 или 0 с помощью ограничивающих линий p1 = [-3; -2]; a1 = sim(net,p1) a1 = 1 1 0 >> p2 = [5; -1]; a2 = sim(net,p2) a2 = 1 0 0 >> p3 = [-1; -3]; a3 = sim(net,p3) a3 = 1 1 0 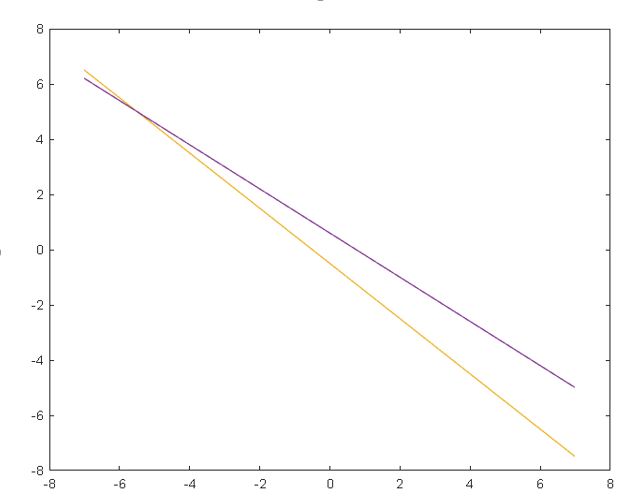 Рисунок 2 .Линии ограничения для входов персептрона Вывод: в ходе выполнения курсовой работы я научился описывать модель персептрона в MATLAB. Ознакомился с моделью нейрона персептрона и архитектурой персептронной однослойной нейронной сети. А также в программе MATLAB я создал и исследовал модель однослойной персептронной нейронной сети, состоящей из 2 нейронов |
