Отчет по лабораторной работе. Отчет лр 2. Лабораторная работа 2 "исследование динамических характеристик типовых линейных звеньев сау"
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №2 "ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ТИПОВЫХ ЛИНЕЙНЫХ ЗВЕНЬЕВ САУ" Цель работы: исследование динамических свойств типовых звеньев систем автоматического регулирования (САР). В процессе работы необходимо научиться по виду дифференциального уравнения звена находить его передаточную функцию и строить динамические характеристики звена (переходную и импульсную переходную характеристики). ЗАДАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ В табл. 2.2 приведены виды типовых звеньев выбранных для анализа в соответствии с номером звена, который указан в табл.2.1. Таблица 2.1
Таблица 2.2
Произвели необходимые подготовительные расчеты, необходимые для моделирования заданных звеньев на компьютере. На основании результатов расчетов и с помощью математической программы MathCAD получили аналитические выражения динамических характеристик указанных звеньев при нулевых и ненулевых начальных условиях. Построили их графики в среде MathCAD. В среде программы MultiSim (приложение пакета программ LabView – приложение для имитационного моделирования) получили схемы моделей и построили динамические характеристики при нулевых и заданных начальных условиях. РАСЧЁТНАЯ ЧАСТЬ 6 ЗВЕНО Нашли аналитическое выражение реакции на входной сигнал 1(t) (единичное ступенчатое воздействие) колебательного звена, описываемого дифференциальным уравнением: при известных параметрах звена и ненулевых начальных условиях (Таблица 2.1). Применили к дифференциальному уравнению обратное преобразование Лапласа (руководствуясь свойствами преобразования Лапласа), получим операторное уравнение звена: Преобразовали полученное уравнение, приведя его к виду: Следует, что передаточная функция данного колебательного звена имеет вид: где W(s) – передаточная функция, которая является изображением импульсной переходной характеристики, Fн.у.(s) – изображение составляющей переходного процесса, соответствующей ненулевым начальным условиям Обратное преобразование Лапласа выполнили, пользуясь таблицами соответствия изображений Лапласа оригиналам или с помощью математических программ, имеющих в своей среде возможность выполнения символьных преобразований (например, программа MathCAD). ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЗВЕНА С ПОМОЩЬЮ СПЕЦИАЛИЗИРОВАННЫХ ПРОГРАММ Построение динамических характеристик в среде программы MathCAD Описание изображений W(s), H(s) и Fн.у.(s): 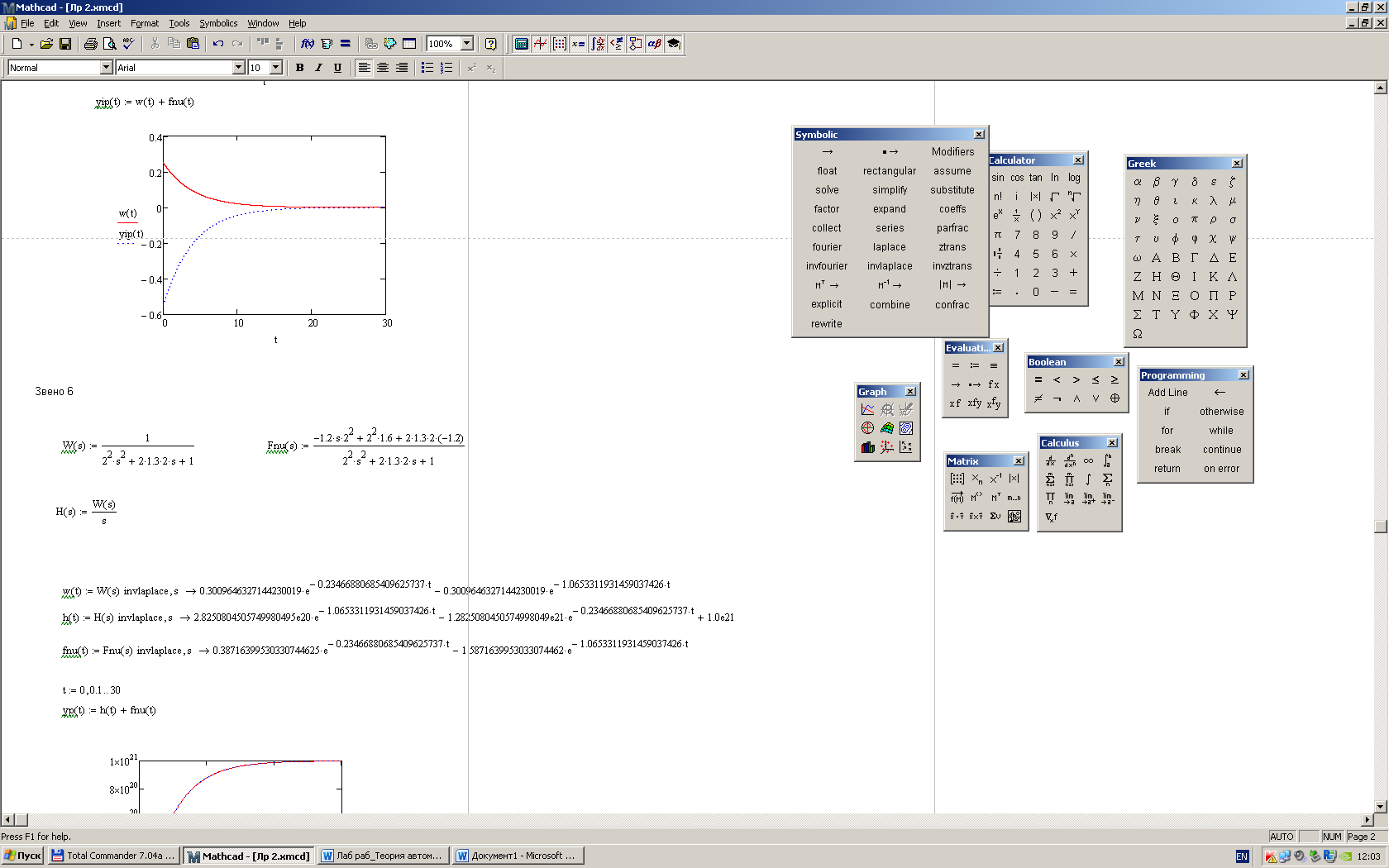 Нахождение аналитического описания (оригиналов) динамических характеристик и составляющей, соответствующей ненулевым начальным условиям:  Для нахождения оригиналов записанных изображений воспользуемся оператором invlaplace, также расположенным на панели Symbolic. При этом мы должны помнить, что w(t) – аналитическая запись импульсной переходной характеристики, т.е. реакции звена на единичное импульсное воздействие при нулевых начальных условиях, а h(t) –переходная характеристика звена, т.е. реакция звена на единичное ступенчатое воздействие при нулевых начальных условиях. В соответствии с выражениями получим описание динамических процессов при ненулевых начальных условиях. Реакция системы на единичный импульс при ненулевых начальных условиях Реакция системы на единичное ступенчатое воздействие при ненулевых начальных условиях Задав с помощью дискретного аргумента диапазон изменения переменной t (время), построим на шаблоне Декартового графика кривые h(t) иw(t), а также yp(t) и yip(t) – соответственно реакция звена на единичное ступенчатое воздействие и единичный импульс при ненулевых начальных условиях. График реакции системы на единичное ступенчатое воздействие при ненулевых и нулевых начальных условиях. 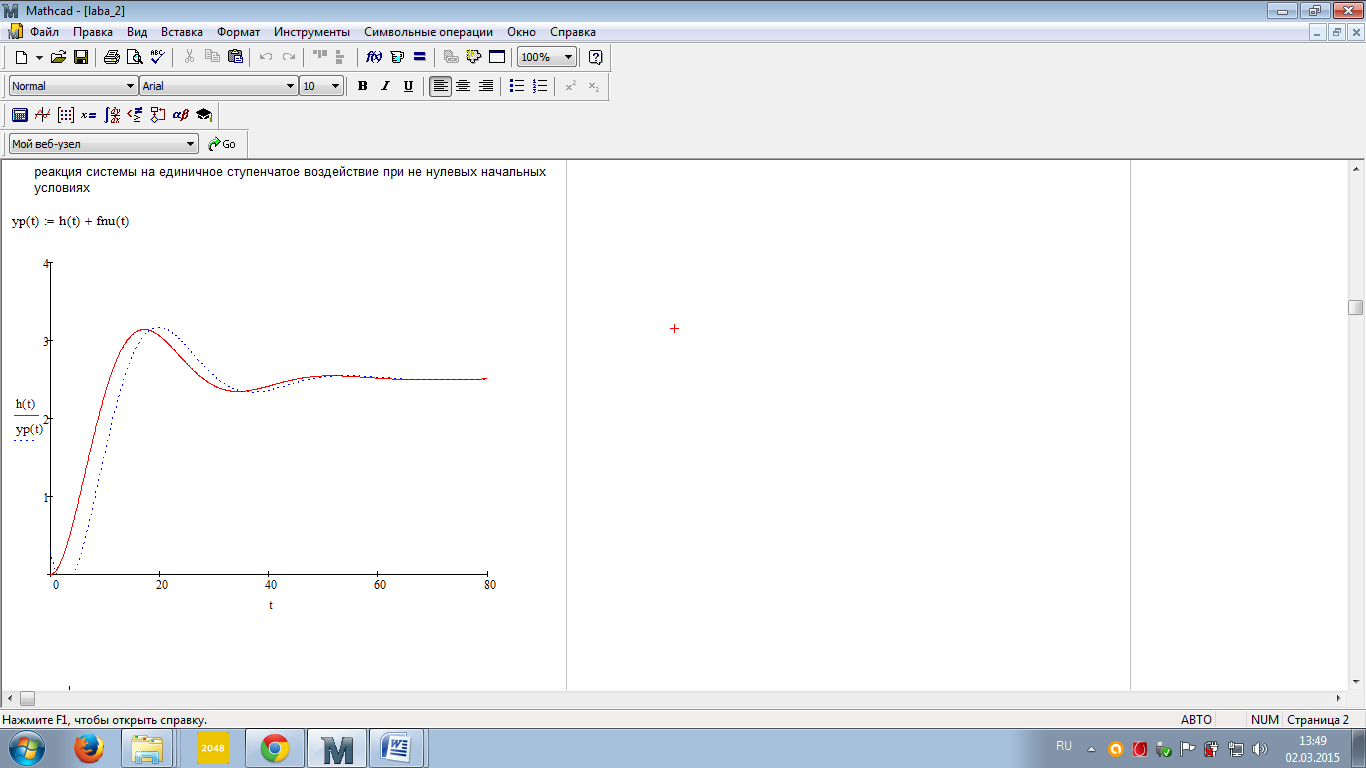 График реакции системы на единичное ступенчатое воздействие при ненулевых и нулевых начальных условиях. 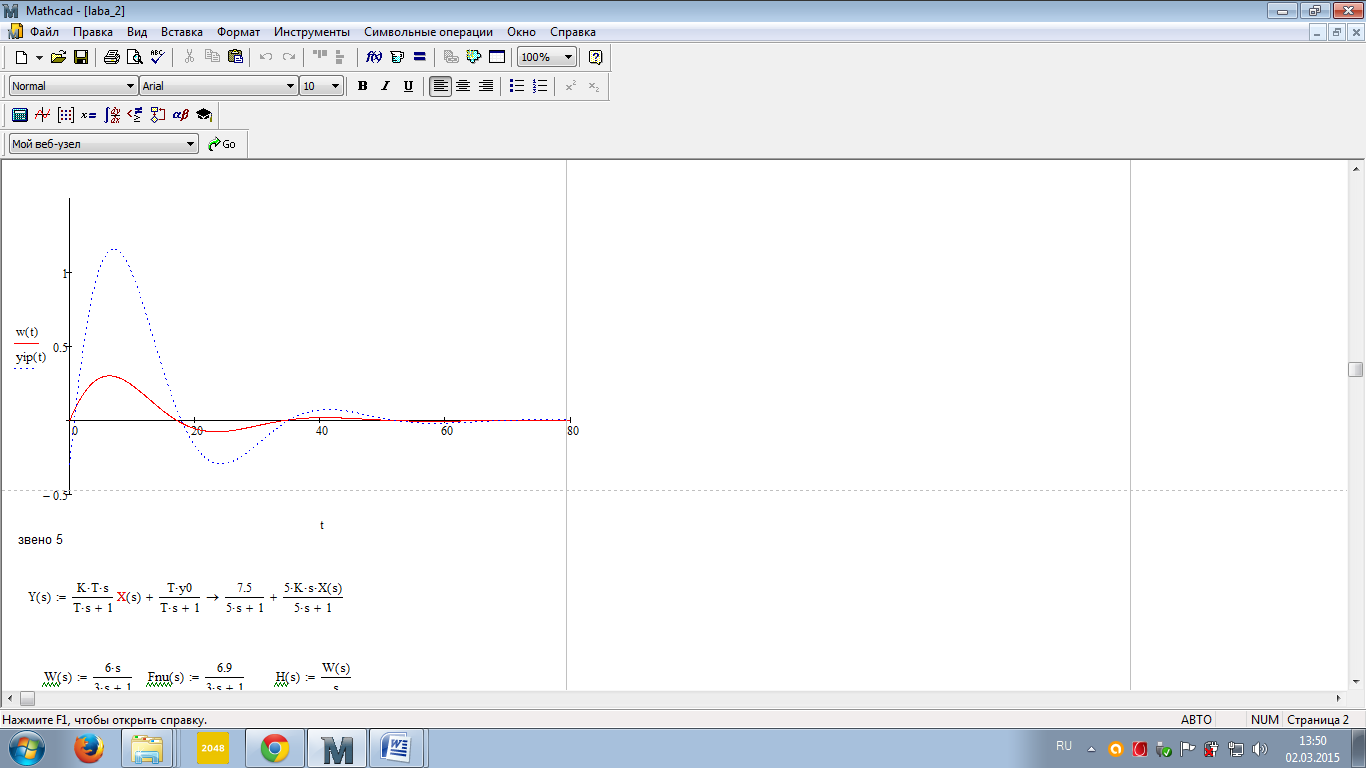 Рис.1.4. Графики динамических характеристик звена Построение динамических характеристик в среде программы Multisim. Запустите программу Multisim. В появившейся пустой рабочей области программы Multisim, соберем схему для исследования реакции звена на единичное ступенчатое воздействие, показанную на рис.1.5. 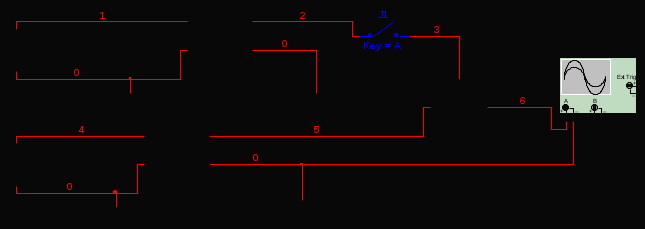 Рис.1.5. Схема для исследования реакции звена на единичное ступенчатое воздействие В данной схеме элементы А1 и А2 построены на основании элемента Transfer function block, использовавшегося в лабораторной работе №1. Задайте параметры элемента А2 в соответствии с параметрами передаточной функции исследуемого звена, т.е. данный элемент представляет собой исследуемое звено. Таблица 2.3
В виду того, что мы исследуем реакцию звена единичное ступенчатое воздействие 1(t), то на вход элемента А2 подадим сигнал напряжения, который при t=0 с нулевого уровня мгновенно увеличивается до 1 В. При разомкнутом выключателе S1 мы получим переходную характеристику звена (нулевые начальные условия), как показано на рис.1.6,а. При замкнутом выключателе S1 получим реакцию звена на единичное ступенчатое воздействие при ненулевых начальных условиях (рис.1.6,б). 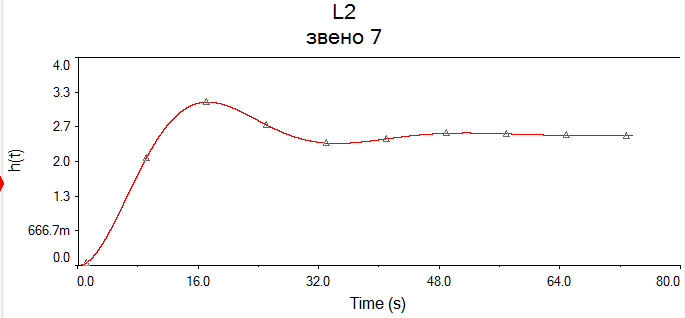 а) 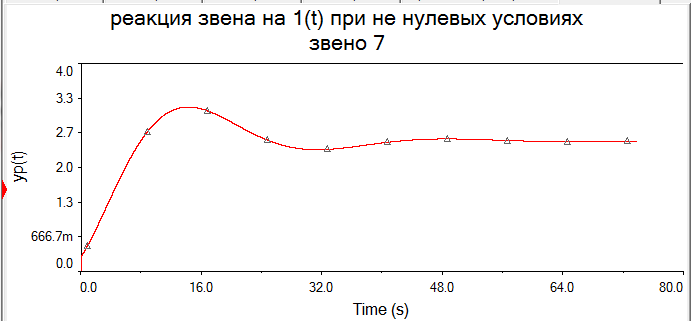 б) Рис.1.6. Графики переходной характеристики звена (а) и реакции звена на единичное ступенчатое воздействие при ненулевых начальных условиях (б) 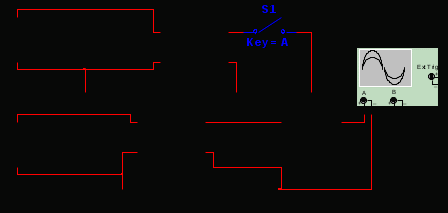 Рис.1.7. Схема для исследования реакции звена на единичное импульсное воздействие Выполнив действия над полученной схемой аналогичные тем, которые производились при построении реакции звена на единичное ступенчатое воздействие, получим в среде Multisim графики импульсной переходной характеристики и реакции звена на единичный импульс при ненулевых начальных условиях. 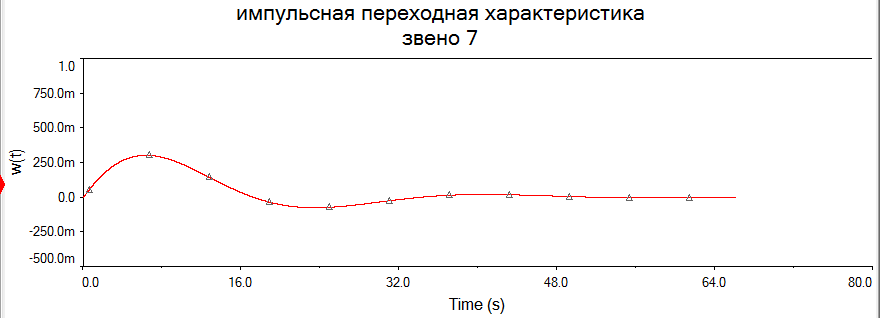 а) 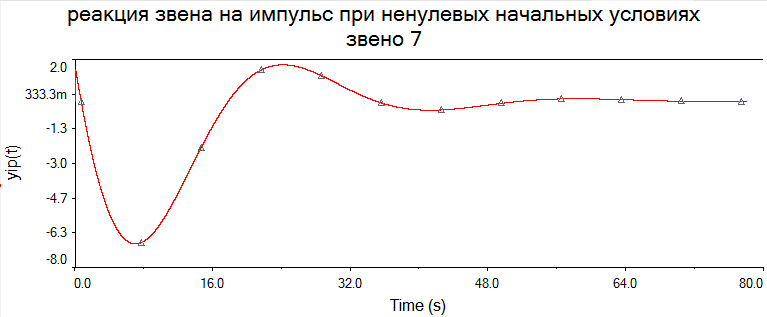 б) Рис.1.8. Графики импульсной переходной характеристики звена (а) и реакции звена на единичное импульсное воздействие при ненулевых начальных условиях (б) РАСЧЁТНАЯ ЧАСТЬ 5 ЗВЕНО Нашли аналитическое выражение реакции на входной сигнал 1(t) (единичное ступенчатое воздействие) колебательного звена, описываемого дифференциальным уравнением: при известных параметрах звена и ненулевых начальных условиях: K = 2.5, T = 5, = 0,4, y(0) = 1.5, y(0) = -2.6. Применили к дифференциальному уравнению обратное преобразование Лапласа (руководствуясь свойствами преобразования Лапласа), получим операторное уравнение звена: где W(s) – передаточная функция, которая является изображением импульсной переходной характеристики, Fн.у.(s) – изображение составляющей переходного процесса, соответствующей ненулевым начальным условиям. Обратное преобразование Лапласа можно выполнили, пользуясь таблицами соответствия изображений Лапласа оригиналам или с помощью математических программ, имеющих в своей среде возможность выполнения символьных преобразований (например, программа MathCAD). ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЗВЕНА С ПОМОЩЬЮ СПЕЦИАЛИЗИРОВАННЫХ ПРОГРАММ Построение динамических характеристик в среде программы MathCAD Перед тем как в документе MathCAD мы зададим вид изображений W(s) и Fн.у.(s), необходимо полином, стоящий в знаменателе передаточной функции W(s) (характеристический полином), разложить на множители. Найдем корни характеристического полинома, для этого воспользуемся оператором solve,расположенным на панели Symbolic (рис.2.7). Рис.2.1. Вычисление корней характеристического полинома  Задав с помощью дискретного аргумента диапазон изменения переменной t (время), построили на шаблоне Декартового графика кривые h(t) иw(t), а также yp(t) и yip(t) – соответственно реакция звена на единичное ступенчатое воздействие и единичный импульс при ненулевых начальных условиях. График реакции системы на единичное ступенчатое воздействие при ненулевых и нулевых начальных условиях. 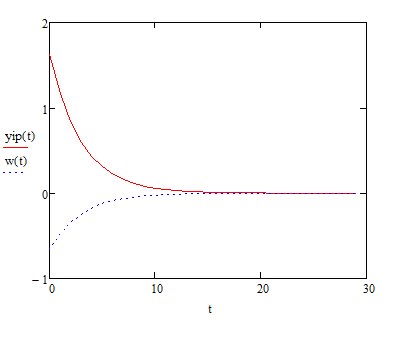 График реакции системы на единичное ступенчатое воздействие при ненулевых и нулевых начальных условиях. 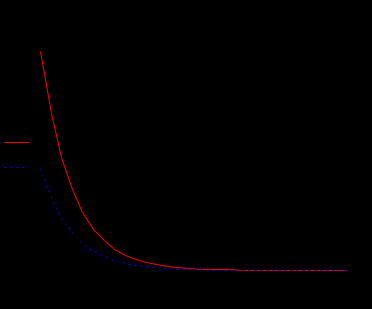 Рис.2.2. Графики динамических характеристик звена Построение динамических характеристик в среде программы Multisim. В появившейся пустой рабочей области программы Multisim, соберем схему для исследования реакции звена на единичное ступенчатое воздействие, показанную на рис.2.3.  Рис.2.3. Схема для исследования реакции звена на единичное ступенчатое воздействие В виду того, что мы исследуем реакцию звена единичное ступенчатое воздействие 1(t), то на вход элемента А2 подадим сигнал напряжения, который при t=0 с нулевого уровня мгновенно увеличивается до 1 В. При разомкнутом выключателе S1 мы получим переходную характеристику звена (нулевые начальные условия), как показано на рис.2.4,а. При замкнутом выключателе S1 получим реакцию звена на единичное ступенчатое воздействие при ненулевых начальных условиях (рис.2.4,б). 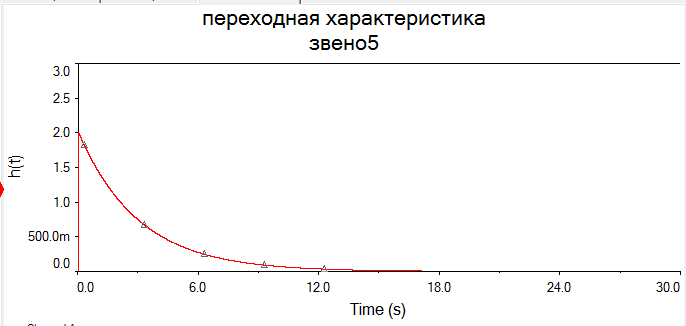 а) 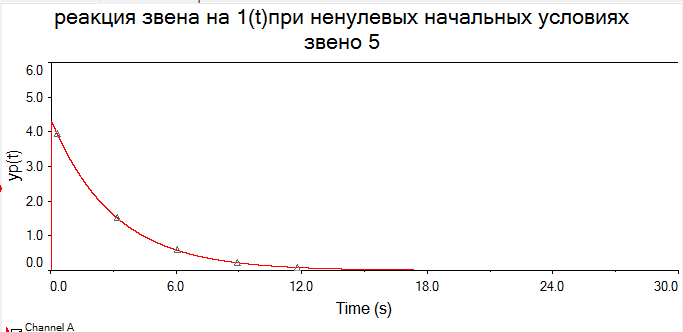 б) Рис.2.4. Графики переходной характеристики звена (а) и реакции звена на единичное ступенчатое воздействие при ненулевых начальных условиях (б)  Рис.2.5. Схема для исследования реакции звена на единичное импульсное воздействие Выполнив действия над полученной схемой аналогичные тем, которые производились при построении реакции звена на единичное ступенчатое воздействие, получим в среде Multisim графики импульсной переходной характеристики и реакции звена на единичный импульс при ненулевых начальных условиях. 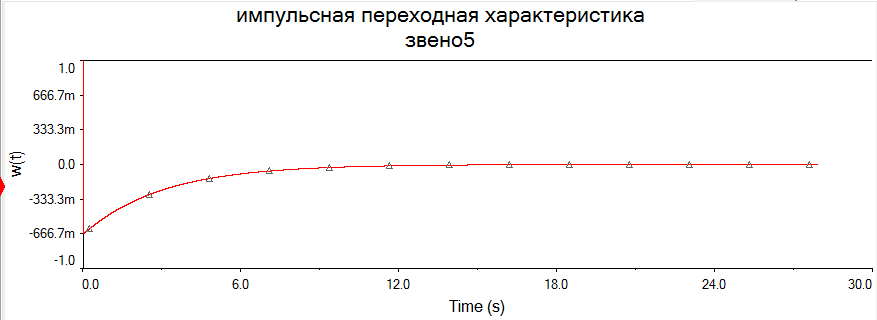 а) 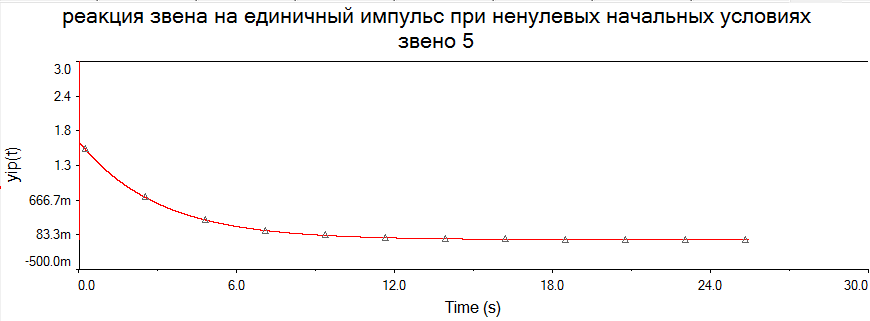 б) Рис.2.5. Графики импульсной переходной характеристики звена (а) и реакции звена на единичное импульсное воздействие при ненулевых начальных условиях (б) РАСЧЁТНАЯ ЧАСТЬ 2 ЗВЕНО Нашли аналитическое выражение реакции на входной сигнал 1(t) (единичное ступенчатое воздействие) колебательного звена, описываемого дифференциальным уравнением: при известных параметрах звена и ненулевых начальных условиях: K = 2.5, T = 5, = 0,4, y(0) = 1.5, y(0) = -2.6 Применили к дифференциальному уравнению обратное преобразование Лапласа (руководствуясь свойствами преобразования Лапласа), получим операторное уравнение звена: где W(s) – передаточная функция, которая является изображением импульсной переходной характеристики, Fн.у.(s) – изображение составляющей переходного процесса, соответствующей ненулевым начальным условиям. Обратное преобразование Лапласа можно выполнили, пользуясь таблицами соответствия изображений Лапласа оригиналам или с помощью математических программ, имеющих в своей среде возможность выполнения символьных преобразований (например, программа MathCAD). ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЗВЕНА С ПОМОЩЬЮ СПЕЦИАЛИЗИРОВАННЫХ ПРОГРАММ Построение динамических характеристик в среде программы MathCAD Перед тем как в документе MathCAD мы зададим вид изображений W(s) и Fн.у.(s), необходимо полином, стоящий в знаменателе передаточной функции W(s) (характеристический полином), разложить на множители. Нашли корни характеристического полинома, для этого воспользуемся оператором solve,расположенным на панели Symbolic . Рис.3.1. Вычисление корней характеристического полинома Задав с помощью дискретного аргумента диапазон изменения переменной t (время), построили на шаблоне Декартового графика кривые h(t) иw(t), а также yp(t) и yip(t) – соответственно реакция звена на единичное ступенчатое воздействие и единичный импульс при ненулевых начальных условиях. Реакция системы на единичный импульс при ненулевых начальных условиях Реакция системы на единичное ступенчатое воздействие при ненулевых начальных условиях График реакции системы на единичное ступенчатое воздействие при ненулевых и нулевых начальных условиях. 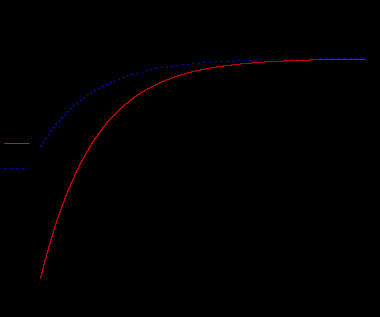 График реакции системы на единичное ступенчатое воздействие при ненулевых и нулевых начальных условиях. 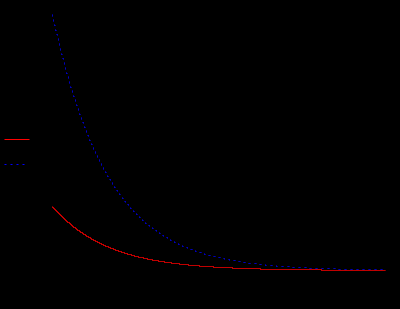 Рис.3.2. Графики динамических характеристик звена Построение динамических характеристик в среде программы Multisim. В появившейся пустой рабочей области программы Multisim, соберем схему для исследования реакции звена на единичное ступенчатое воздействие, показанную на рис.3.3.  Рис.3.3. Схема для исследования реакции звена на единичное ступенчатое воздействие В виду того, что мы исследуем реакцию звена единичное ступенчатое воздействие 1(t), то на вход элемента А2 подадим сигнал напряжения, который при t=0 с нулевого уровня мгновенно увеличивается до 1 В. При разомкнутом выключателе S1 мы получим переходную характеристику звена (нулевые начальные условия), как показано на рис.3.4,а. При замкнутом выключателе S1 получим реакцию звена на единичное ступенчатое воздействие при ненулевых начальных условиях (рис.3.4,б). 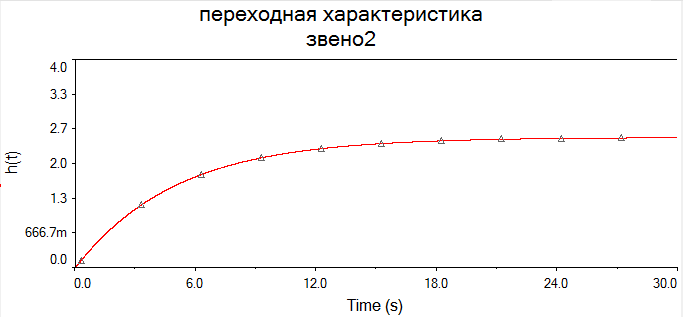 а) 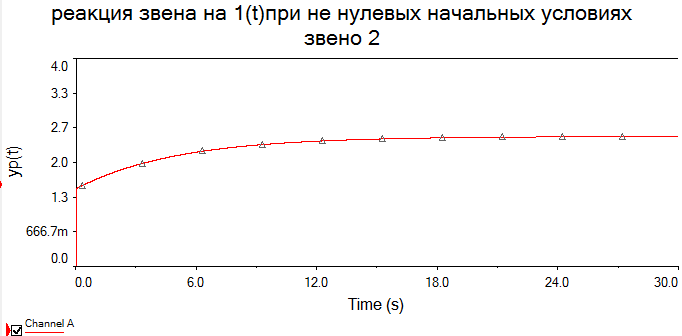 б) Рис.3.4. Графики переходной характеристики звена (а) и реакции звена на единичное ступенчатое воздействие при ненулевых начальных условиях (б)  Рис.3.6. Схема для исследования реакции звена на единичное импульсное воздействие Выполнив действия над полученной схемой аналогичные тем, которые производились при построении реакции звена на единичное ступенчатое воздействие, получили в среде Multisim графики импульсной переходной характеристики и реакции звена на единичный импульс при ненулевых начальных условиях. 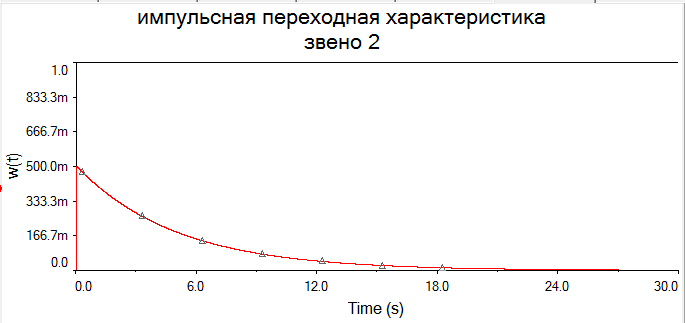 а) 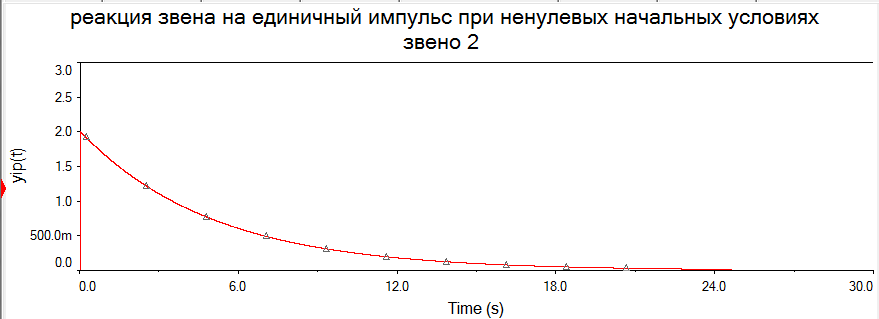 б) Рис.3.7. Графики импульсной переходной характеристики звена (а) и реакции звена на единичное импульсное воздействие при ненулевых начальных условиях (б) Вывод: | ||||||||||||||||||||||||||||||||||||||||||||
