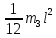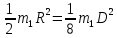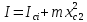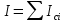лр 2. лаба 2. Лабораторная работа 2 исследование динамики свободных гармонических колебаний в поле силы тяжести
 Скачать 46.29 Kb. Скачать 46.29 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 2 «ИССЛЕДОВАНИЕ ДИНАМИКИ СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ В ПОЛЕ СИЛЫ ТЯЖЕСТИ» 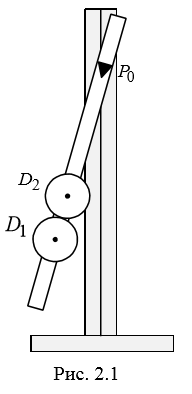 ЦЕЛЬ РАБОТЫ: изучение закономерностей колебательного движения тела в однородном поле силы тяжести; исследование процессов превращения энергии в консервативных системах; определение момента инерции физического маятника. СХЕМА УСТАНОВКИ: Конструкция оборотного маятника представлена на рис. 2.1. На стержне 1 закреплены два диска – D1 и D2. Маятник может быть подвешен на кронштейне к легкой призме, трение в которой пренебрежимо мало. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: физический маятник; секундомер; масштабная линейка, чертежный треугольник. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Период колебания маятника .  Момент инерции маятника I =  Полный момент инерции маятника 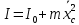 Где  ; ;  – средний квадрат положений центров масс системы тел, составляющих маятник – средний квадрат положений центров масс системы тел, составляющих маятникЕсли период колебаний маятника определен экспериментально, то из п.1 можно найти момент инерции маятника I =  Полная механическая энергия маятника 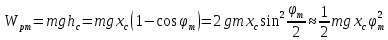  - максимальный угол отклонения(< - максимальный угол отклонения(< 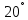 ) )Приведенная длинна маятника 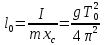 Объём цилиндра диаметром D и длинной(высотой) h  Масса цилиндраобъёмом V 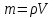 ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА ПУНКТ 1. N=5 P=95% 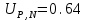 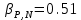 
 < <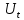 -промахов нет -промахов нет
ПУНКТ 2 N=5 P=95%  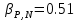 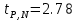 T=t/n
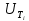 < <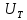 -промахов нет -промахов нет
ПУНКТ 3 N=5 P=95% 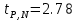 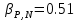 (f= (f=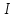 ) )I=  , , 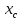 =0.392 =0.392
ПУНКТ 4  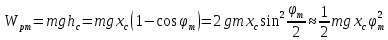
ПУНКТ 5
ПУНКТ 6
ПУНКТ 7
Несильно отличается от значения, определенного экспериментально (0.392 м) ПУНКТ 8 L=0.12 м
Результат момента инерции с учетом погрешности соответствует полученному экспериментально в п. 3 (0.2266 кг*  ) ) ВОПРОСЫ: 1)Колебания гармонические, если происходят по синусоидальному закону. При малом  справедливо sin справедливо sin 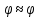 2)Физический маятник – подвешенное на нерастяжимой нити тело, колеблющееся за счет своей силы тяжести. Математический – частный случай физического, идеализированная система, тело представляет собой материальную точку. Длинна математического маятника, период которого совпадает с периодом колебаний данного физического маятника называется приведенной длинной физического маятника. Её можно найти экспериментально, если найти новую ось  , называемую осью качания, относительно которой маятник колеблется с тем же периодом , называемую осью качания, относительно которой маятник колеблется с тем же периодом 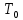 , что и относительно оси вращения O. Расстояние между осями вращения и качания O , что и относительно оси вращения O. Расстояние между осями вращения и качания O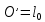 и будет приведенной длиной физического маятника. и будет приведенной длиной физического маятника.3)Центр масс (центр инерции) – геометрическая точка имеющая координаты 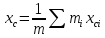 Характеризует распределение масс системы 4) Момент инерции -скалярная физическая величина, мера инертности во вращательном движении вокруг оси  Момент инерции составного тела 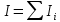 5)Конструкция оборотного маятника представлена на рис. 2.1. На стержне 1 закреплены два диска – D1 и D2. Маятник может быть подвешен на кронштейне к легкой призме, трение в которой пренебрежимо мало. Измерения проводятся, как прямым образом ( чертежная линейка, транспортир, секундомер) , так и косвенным ( 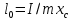 ) )6)Момент инерции зависит от размеров, массы тела и от оси вращения  7)  – угловая скорость, а значит и угловое ускорение НЕ зависит от расстояния точки от центра вращение. – угловая скорость, а значит и угловое ускорение НЕ зависит от расстояния точки от центра вращение.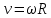 – а вот линейная скорость, а значит и ускорение, увеличивается по мере удаления материальной точки от центра вращения – а вот линейная скорость, а значит и ускорение, увеличивается по мере удаления материальной точки от центра вращения8)Колебание математического маятника можно описать законом сохранения энергии  как консервативную систему и элементарным законом гармонического колебания тела x=Asin как консервативную систему и элементарным законом гармонического колебания тела x=Asin , T=t/n , T=t/n9) x(t)=Asin  x - координата точки в момент времени t А - амплитуда  - угловая скорость тела, содержащая частоту ν - угловая скорость тела, содержащая частоту ν – фаза – фаза10) Из закона сохранения полной механической энергии  ВЫВОДЫ: Мы рассмотрели закономерности колебания тела в однородном поле тяжести, проследили отличие физического маятника от математического, исследовали процессы превращения энергии в консервативных системах. Научились определять моменты инерции физического маятника, в том числе составного |

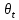 =0.005
=0.005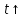 , c
, c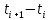
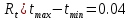
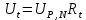 =0.0256
=0.0256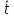 =
=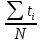

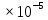
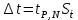
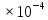
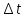 =
=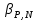


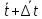
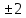 )
)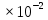
 =0.0005
=0.0005 , c
, c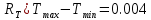

 =0,00256
=0,00256 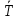 =
=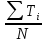

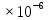

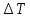 =
=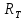
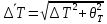

 =
=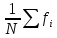
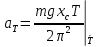
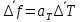
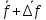
 )
)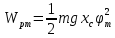
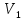 =
=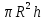 =1/4(
=1/4(
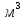
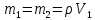
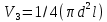

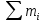
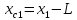

 м
м
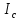 )
)