Лабораторная работа. Три лабы Вариант 1. Лабораторная работа 2 исследование сложной резистивной цепи цель работы
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
1 2 Экспериментальная часть 1. Соберём электрическую цепь по рабочей схеме (Рис. 7.7). Установим заданные параметры отдельных элементов. Для каждого из заданных значений емкости конденсатора С при ZН = const измерим токи в отдельных ветвях схемы, напряжения на отдельных участках, а также мощность источника Р1. Результаты измерений внесём в таблицу. 7.3. Рассчитаем РR1, Рн и φэ 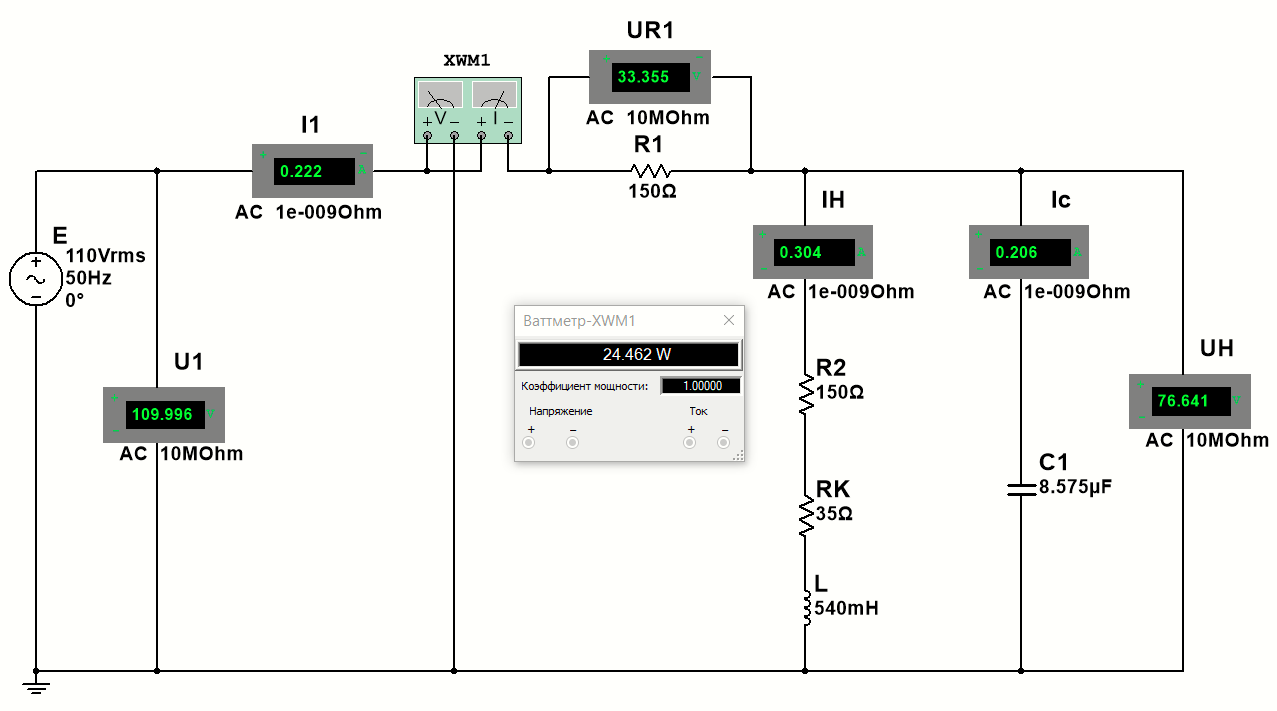 Рис 7.7 C = 0 мкФ 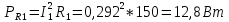 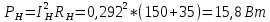 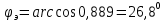 C = 2,144 мкФ 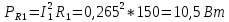 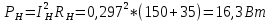 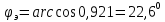 C = 4,288 мкФ 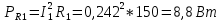 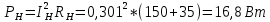 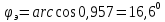 C = 6,431 мкФ 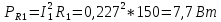 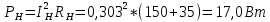 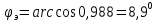 C = 8,575 мкФ 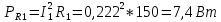 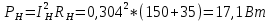 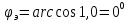 C = 10,719 мкФ 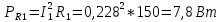 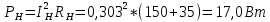  Таблица 7.3
1. Сравнивая результаты расчётов и результаты экспериментов убеждаемся, что они в основном соответствуют друг другу (незначительные расхождения обусловлены погрешностями при округлениях и внесением искажений включение измерительных приборов). 2. Если нагрузка сети обладает постоянным значением cosφ, то целесообразно реактивную мощность компенсировать полностью. Если нагрузка сети обладает непостоянным значением cosφ, то целесообразно реактивную мощность расчитывать по среднему значению cosφ. Лабораторная работа № 8 ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ НАГРУЗКИ ЗВЕЗДОЙ С НУЛЕВЫМ ПРОВОДОМ Цель работы: 1) изучение методов расчета схемы трехфазной цепи, соединенной звездой с нулевым проводом; 2) исследование влияния симметрии и характера нагрузки на симметрию линейных (фазных) токов и ток в нулевом проводе; 3) построение векторных диаграмм токов и напряжений для трехфазной цепи. Дано Задана схема (Рис 8.1) 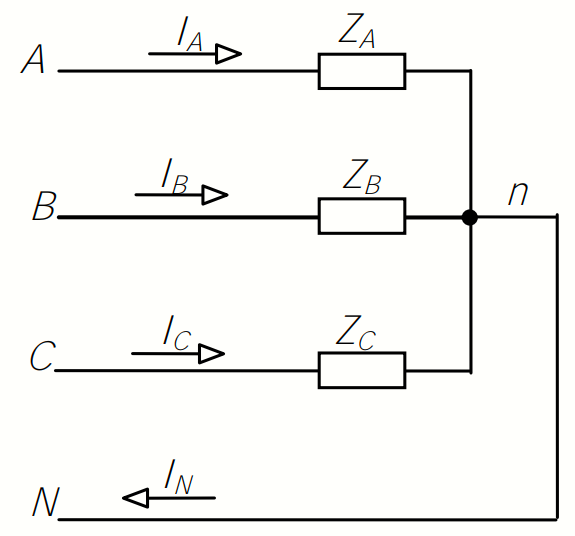 Рис 8.1 Линейное и фазное напряжение 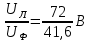 1. Симметричная нагрузка 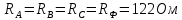 2. Несимметричная однородная нагрузка 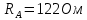  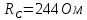 3. Несимметричная неоднородная нагрузка 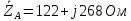 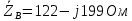 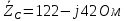 Решение Запишем значения фазных напряжений в комплексном виде в алгебраической и показательной формах. Так как начальные значения фаз не указаны, примем что фаза А имеет нулевое значение, тогда фазы В и С сдвинуты по отношению к фазе А на 120 и 240 градусов соответственно 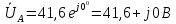 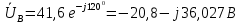 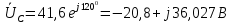 1. Произведём расчёт схемы трехфазной цепи для симметричной нагрузки 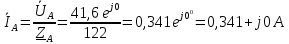 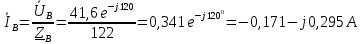  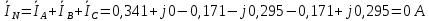 Активная мощность каждой фазы 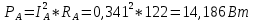 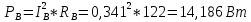 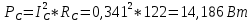 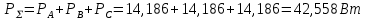 2. Произведём расчёт схемы трехфазной цепи для не симметричной нагрузки 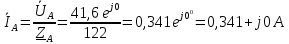 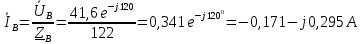  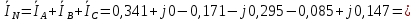 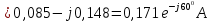 Активная мощность каждой фазы 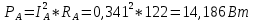 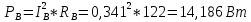 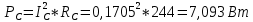 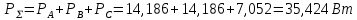 3. Несимметричная неоднородная нагрузка 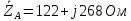 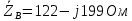 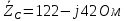 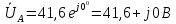 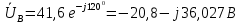 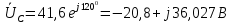 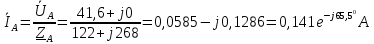 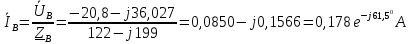 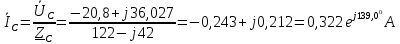 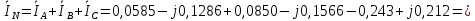 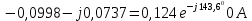 Активная мощность каждой фазы 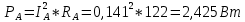 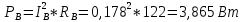 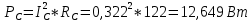 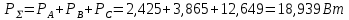 Результаты расчётов запишем в таблицы 8.2 и 8.3 Для каждого вида нагрузки построим векторные диаграммы токов и напряжений (Рис 8.2, 8.3 и 8.4) 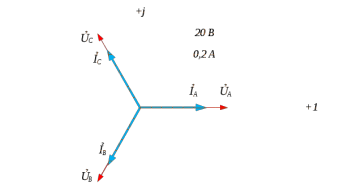 Рис 8.2  Рис 8.3  Рис 8.4 Таблица 8.2
1. Соберём электрическую схему с симметричной нагрузкой в среде виртуальной лаборатории Multisim (Рис 8.5) и произведём измерения линейных (фазных) токов IА, IB, IС и тока в нулевом проводе IN. Модули комплексных токов измерим амперметром. Результаты измерений запишем в табл. 8.2. Измерим активные мощности фаз нагрузки РА, РB РС (ваттметром). Результаты измерений запишем в табл. 8.3. 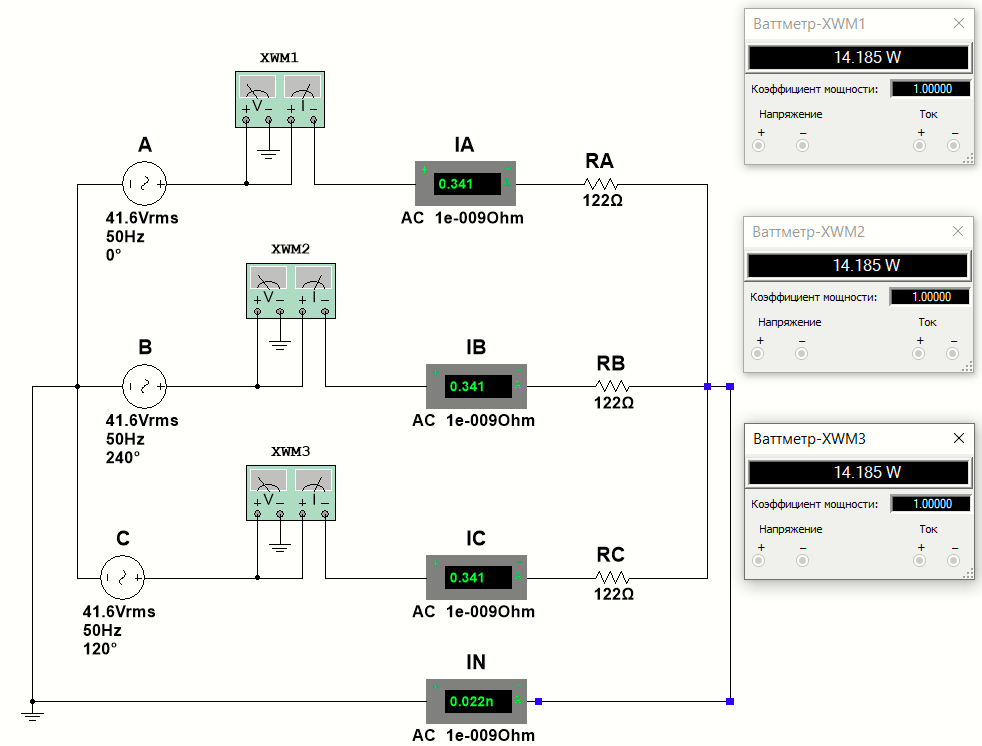 Рис 8.5 2. Соберём электрическую схему с несимметричной нагрузкой в среде виртуальной лаборатории Multisim (Рис 8.6) и произведём измерения линейных (фазных) токов IА, IB, IС и тока в нулевом проводе IN. Модули комплексных токов измерим амперметром. Результаты измерений запишем в табл. 8.2. Измерим активные мощности фаз нагрузки РА, РB РС (ваттметром). Результаты измерений запишем в табл. 8.3. 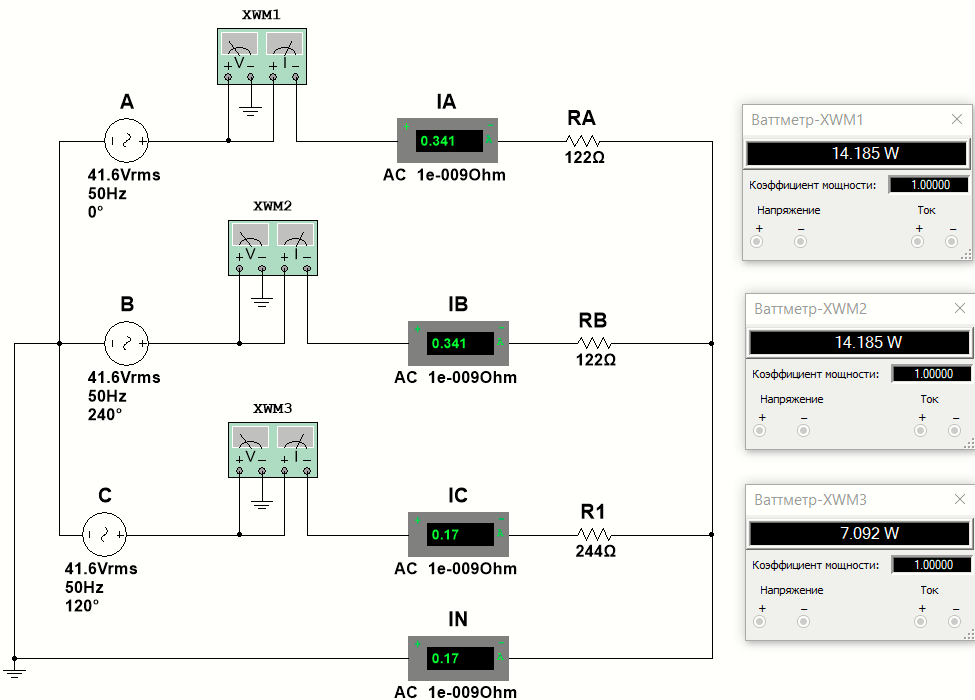 Рис 8.6 Определим величину индуктивности и ёмкости в ветвях схемы 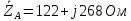 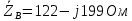 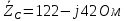 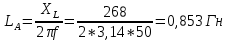  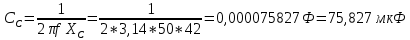 3. Соберём электрическую схему с неоднородной нагрузкой в среде виртуальной лаборатории Multisim (Рис 8.7) и произведём измерения линейных (фазных) токов IА, IB, IС и тока в нулевом проводе IN. Модули комплексных токов измерим амперметром. Результаты измерений запишем в табл. 8.2. Измерим активные мощности фаз нагрузки РА, РB РС (ваттметром). Результаты измерений запишем в табл. 8.3. 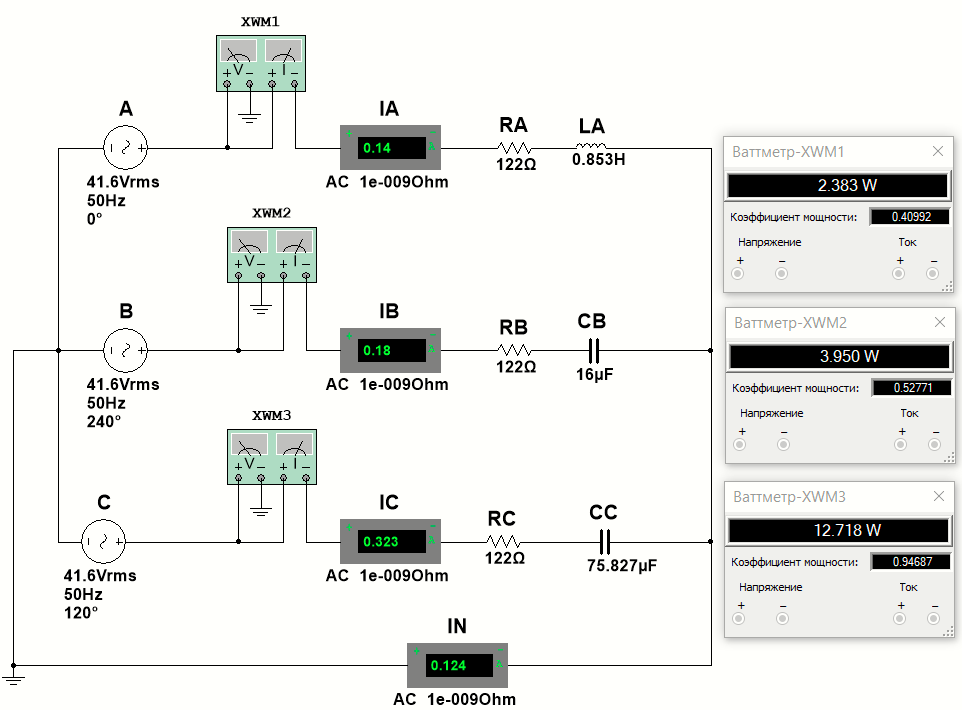 Рис 8.7 Выводы Сравнивая результаты эксперимента с результатами расчётов, убеждаемся, что они в основном соответствуют друг другу (незначительные расхождения обусловлены погрешностями при округлениях и внесением искажений измерительными приборами. 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||