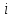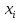НАИЛУЧШАЯ АППРОКСИМАЦИЯ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЯ.. Лабораторная работа 2 наилучшая аппроксимация результатов наблюдения. Постановка задачи
 Скачать 47.65 Kb. Скачать 47.65 Kb.
|
|
Лабораторная работа №2 НАИЛУЧШАЯ АППРОКСИМАЦИЯ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЯ. 1.1.Постановка задачи Используя метод наименьших квадратов для опытных данных, определить наилучшую аппроксимацию из набора 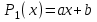 , , 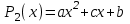 , , 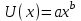 , , 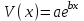 . . Значения координат точек приведены в таблице 1.1 Координаты точек Таблица1.1
Построить заданные точки и наилучшую аппроксимирующую кривую. 1.2 Теоретический материал Поиск параметров аппроксимирующих функций происходит с использованием метода наименьших квадратов (МНК). В методе разыскивается минимум функций, составленный в виде суммы квадратов отклонений теоретических значений от экспериментальных. 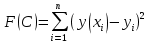 (1.2) (1.2)С учётом (1.1) формула (1.2) перепишется: 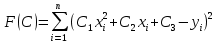 (1.3) (1.3)Минимум функции (1.3) ищется из условий равенства нуля и ее частных производных по неизвестным квадратам. 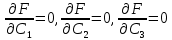 (1.4) (1.4)Вычисляя производные получим следующие системы линейных алгебраических уравнений (СЛАУ). 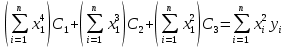  (1.5) (1.5)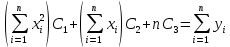 В матричном виде система (1.5) запишется в виде: 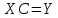 (1.6) (1.6)Где 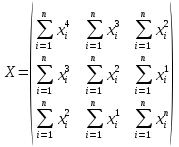 , , 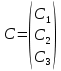 , , 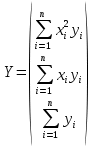 (1.7) (1.7)Решение параметров аппроксимирующей функции по МНК сводится к решению СЛАУ (1.6) с матрицами (1.7). МНК можно использовать для функций, которые не являются полиномами, но для этого изменяют начальные данные. Проводят линиаризацию. 1.3 Программирование МНК в Mathcad Для построения аппроксимирующей функции в Mathcad необходимо следовать следующему алгоритму. Задаём n – количество координат. Но не забываем, что отсчёт в программе ведётся с 0, поэтому задаём на одно значение меньше. С помощью встроенной функции READPRN вывести в программу полученные столбцы х и у. Так как аппроксимация P1(x) и P2(x) похожи, то объединим их в одну программу. P1 присваиваем Add line и начинаем программу. Присваиваем Xk,j и Yk формулы  и и  соответственно. K и j задаём от 0 и в первом случае до 1 (так как Р1(х)- полином первого порядка), а во втором соответственно до 2 соответственно. K и j задаём от 0 и в первом случае до 1 (так как Р1(х)- полином первого порядка), а во втором соответственно до 2С помощью формулы (1.5) вычисляем C и С2. Записываем формулы полиномов Р1(х) и Р2(х). 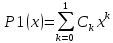 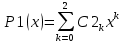 Находим среднеквадратичное отклонение Q для каждого полинома по формуле: 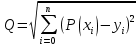 Так как мы можем вывести только одно значение, а нам нужно вывести Q1, Q2, P1, P2, то выведем всё матрицей Н. Нd,0 (где d- строки от 0 до n, а 0 – первый столбец) присваиваем P1(xd). Второму столбцу присваиваем значение Q1, третьему – значение P2(xd), а четвертому – Q2. Выводим матрицу Н . P10,1 выдаст нам значение Q1, P10,3 соответственно Q2. Строим два графика. На одном по оси «игрек» задаём y (начальная функция) и Р1(0) – первый столбец матрицы (значения P1(x)), а по оси «иксов» - x. На втором всё так же, но вместо Р1(0) - Р1(2) Так как аппроксимация U(x) и V(x) похожи, то объединим их в одну программу. Логарифмируем значения x и y. Далее делаем всё тоже самое как для полинома 1 порядка. Когда нашли C3 и С4 вводи а3 и а4 и присваиваем им 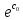 . .Записываем: 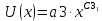 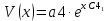 Среднеквадратичное отклонение Q3, Q4 находим по формуле выше. Далее вводим так же матрицу и выводим её. Проводим все те же действия и выводим графики. Программа и полученные графики приведены на рис.1.1.     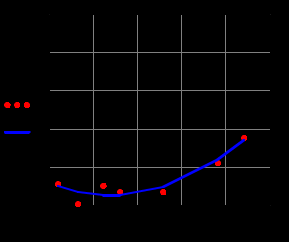 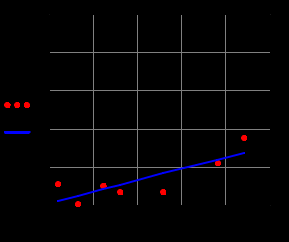 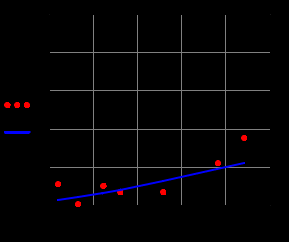 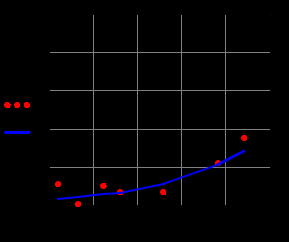 Рис.1.1. Решение в Mathcad 1.4 Вывод В данной работе мы аппроксимировали данные в программе Matchad, из получившихся результатов построили графики. Наилучшей аппроксимацией оказался  . Данный вывод был сделан по значению среднеквадратичного отклонения (оно наименьшее из всех), так же это наглядно видно по графикам. . Данный вывод был сделан по значению среднеквадратичного отклонения (оно наименьшее из всех), так же это наглядно видно по графикам. |