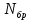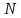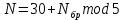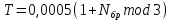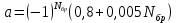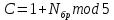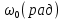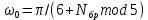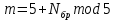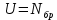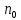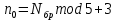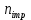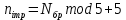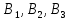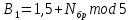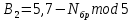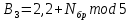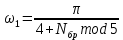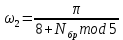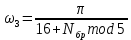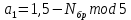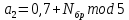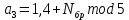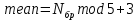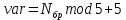ЦОС ЛР№2. Лабораторная работа 2 по дисциплине Цифровая обработка сигналов Моделирование и детерминированных и случайных дискретных сигналов
 Скачать 6.32 Mb. Скачать 6.32 Mb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ Ордена трудового красного знамени федеральное государственное бюджетное образовательное учреждение высшего образования «МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ» (МТУСИ) Лабораторная работа №2 по дисциплине Цифровая обработка сигналов «Моделирование и детерминированных и случайных дискретных сигналов» Выполнили студенты группы БРМ1902 Гайдаров С.А., Исаев О.В. Москва 2021 Цель работы: Изучить математическое описание дискретных сигналов и овладеть программными средствами моделирования в MATLAB. Подготовка к лабораторной работе: 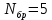 Таблица 2.1 Таблица исходных данных
Код программы: % ЛР №2. ДИСКРЕТНЫЕ СИГНАЛЫ % % % Введите ИСХОДНЫЕ ДАННЫЕ Nb = 5 N = 30 T = 0.0015 a = -0.825 C = 1 w0 = 0.52 m = 5 U = 5 n0 = 4 n_imp = 5 B = [1.5 5.7 2.2] w = [0.7854 0.3927 0.1963] A = [1.5 0.7 1.5] Mean = 3 Var = 5 % Проверьте ПРАВИЛЬНОСТЬ ввода ИСХОДНЫХ ДАННЫХ % При ПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 1 % При НЕПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 0 и ПОВТОРИТЕ ввод --> 1 % % % Для продолжения нажмите % % % п.1. ЦИФРОВОЙ ЕДИНИЧНЫЙ ИМПУЛЬС % % % Для вывода ГРАФИКОВ цифрового единичного импульса нажмите % % % Для продолжения нажмите % % % п.2. ЦИФРОВОЙ ЕДИНИЧНЫЙ СКАЧОК % % % Для вывода ГРАФИКОВ цифрового единичного скачка нажмите % % % Для продолжения нажмите % % % п.3. ДИСКРЕТНАЯ ЭКСПОНЕНТА % % % Для вывода ГРАФИКОВ дискретной экспоненты нажмите % % % Для продолжения нажмите % % % п.4. ДИСКРЕТНЫЙ КОМПЛЕКСНЫЙ ГАРМОНИЧЕСКИЙ СИГНАЛ % % % Для вывода ГРАФИКОВ вещественной и мнимой частей % гармонического сигнала нажмите % % % Для продолжения нажмите % % % п.5. ЗАДЕРЖАННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ % % % Для вывода ГРАФИКОВ задержанных последовательностей нажмите % % % Для продолжения нажмите % % % п.6. ДИСКРЕТНЫЙ ПРЯМОУГОЛЬНЫЙ ИМПУЛЬС % % % Для вывода ГРАФИКОВ дискретного прямоугольного импульса нажмите % % % Для продолжения нажмите % % % п.7. ДИСКРЕТНЫЙ ТРЕУГОЛЬНЫЙ ИМПУЛЬС % % % Для вывода ГРАФИКА дискретного треугольного импульса нажмите % % % Для продолжения нажмите % % % п.8. ЛИНЕЙНАЯ КОМБИНАЦИЯ ДИСКРЕТНЫХ ГАРМОНИЧЕСКИХ СИГНАЛОВ % % % Для вывода ГРАФИКОВ гармонических сигналов и их линейной комбинации нажмите % % % Для вывода СРЕДНЕГО ЗНАЧЕНИЯ, ЭНЕРГИИ и СРЕДНЕЙ МОЩНОСТИ сигнала x5 нажмите % % mean_x5 = 0.29493 E = 2330.4782 P = 15.5365 % % % Для продолжения нажмите % % % п.9. ДИСКРЕТНЫЙ ГАРМОНИЧЕСКИЙ СИГНАЛ С ЭКСПОНЕНЦИАЛЬНОЙ ОГИБАЮЩЕЙ % % % Для вывода ГРАФИКА гармонического сигнала с экспоненциальной огибающей нажмите % % % Для продолжения нажмите % % % п.10. ПЕРИОДИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ДИСКРЕТНЫХ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ % % % Для вывода ГРАФИКА пяти периодов последовательности нажмите % % % Для продолжения нажмите % % % п.11. РАВНОМЕРНЫЙ БЕЛЫЙ ШУМ % % % Для вывода ОЦЕНОК МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ и ДИСПЕРСИИ ШУМА нажмите % % mean_uniform = 0.49956 var_uniform = 0.08291 % % % Для вывода графика АВТОКОВАРИАЦИОННОЙ ФУНКЦИИ нажмите % % % Для продолжения нажмите % % % п.12. НОРМАЛЬНЫЙ БЕЛЫЙ ШУМ % % % Для вывода ОЦЕНОК МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ и ДИСПЕРСИИ шума нажмите % % mean_norm = 0.0018848 var_norm = 0.97502 % % % Для вывода графика АКФ нажмите % % % Для продолжения нажмите % % % п.13. АДДИТИВНАЯ СМЕСЬ ДИСКРЕТНОГО ГАРМОНИЧЕСКОГО СИГНАЛА С НОРМАЛЬНЫМ БЕЛЫМ ШУМОМ % % % Для вывода ГРАФИКА аддитивной смеси сигнала с шумом нажмите % % % Для продолжения нажмите % % % п.14. АКФ АДДИТИВНОЙ СМЕСИ ДИСКРЕТНОГО ГАРМОНИЧЕСКОГО СИГНАЛА С НОРМАЛЬНЫМ БЕЛЫМ ШУМОМ % % % Для вывода ГРАФИКА АКФ нажмите % % % Для вывода ДИСПЕРСИИ аддитивной смеси сигнала с шумом и АКФ R(N) нажмите % % var_x8 = 1.9088 R(N) = 1.8453 % % % Для продолжения нажмите % % % п.15. НОРМАЛЬНЫЙ БЕЛЫЙ ШУМ С ЗАДАННЫМИ СТАТИСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ % % % Для вывода ГРАФИКОВ нормального белого шума нажмите % % % Для вывода ГИСТОГРАММ нормального белого шума нажмите % % % РАБОТА ЗАВЕРШЕНА >> Выполнение: Цифровой единичный импульс u0 (nT) (идентификатор u0) : 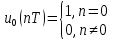 (2.1) (2.1)Графики (рис.1) и (рис.2) на интервале дискретного времени nT (идентификатор nT) 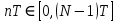 (2.2) (2.2)И дискретного нормированного времени n (идентификатор n) 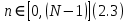  Рис.1 Рис.2 Цифровой единичный скачок u1(nT) (идентификатор u1) 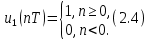 Графики (рис.3) и (рис.4) с интервалом времени (2.2) и (2.3) Р 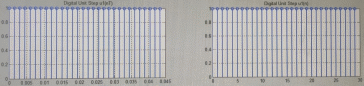 ис.3 Рис.4 ис.3 Рис.4Дискретная экспонента x1(nT) (идентификатор x1) 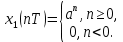 (2.5) (2.5)Графики (рис.5) и (рис.6) с интервалом времени (2.2) и (2.3) Р 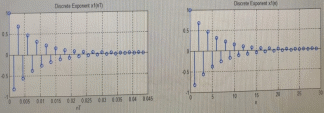 ис.5 ис.5 Рис.6 Дискретный комплексный сигнал x2(n) (идентификатор x2) 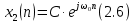 Графики вещественной и мнимой частей (рис.7) и (рис.8) на интервале времени (2.3) 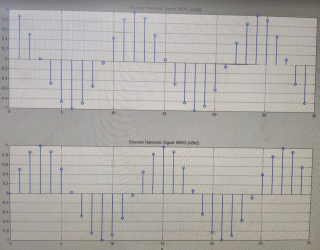 Рис.7 Рис.8 Задержанные последовательности Графики (рис.8), (рис.9) и (рис.10) последовательностей (2.1), (2.4) и (2.5) задержанных на m от счетов (идентификаторы u0_m, u1_m и x1_m), на интервале времени (2.3) 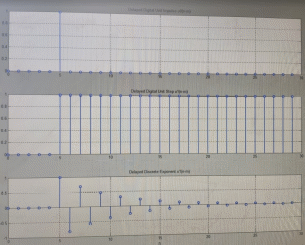 Рис.8 Рис.9 Рис.10 Дискретный прямоугольный импульс x3(n) 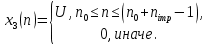 (2.7) (2.7)Графики на интервале времени (2.3): С помощью функции rectpuls – идентификатор x3_1 (рис.11) На основе цифрового единичного скачка – идентификатор x3_2 (рис.12) 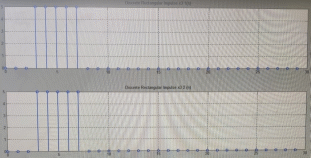 Дискретный треугольный импульс График дискретного треугольного импульса (рис.13) x4(n) (идентификатор x4), сформированного посредством сверки дискретного прямоугольного импульса x3(n) (2.7) с самим собой, на интервале времени, равным длине сверки L 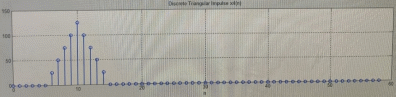 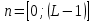 (2.8) (2.8)Рис.13 Линейная комбинация дискретных гармонических сигналов x5(n) (идентификатор x5) 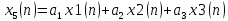 (2.9) (2.9)Где  (2.10) (2.10)Вывод графиков последовательностей (рис.14), (рис.15), (рис.16), (рис.17) xi(n) на интервале времени 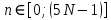 (2.11) (2.11)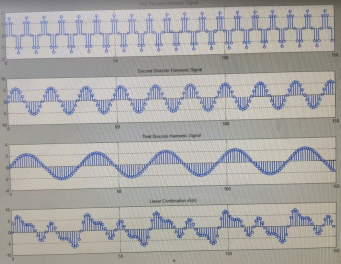 Рис.14 Рис.15 Рис.16 Рис.17 mean_x5 = 0.61594 E = 125093.7149 P = 735.8454 Дискретный гармонический сигнал с экспоненциальной огибающей. График дискретного сигнала (рис.18) x6(n) (идентификатор x6), представляющего собой дискретный гармонический сигнал x(n) (идентификатор x) с экспоненциальной огибающей 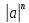 на интервале времени (2.12) на интервале времени (2.12)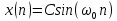 (2.12) (2.12)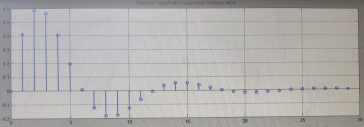 Рис.18 Периодическая последовательность дискретных прямоугольных импульсов. График пяти периодов периодической последовательности x7(n) (идентификатор x7) дискретных прямоугольных импульсов амплитуды Uи длительности nimp, вдвое больше длительности импульса (рис.19). 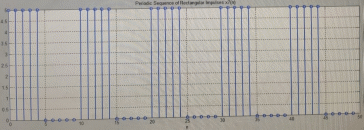 Рис.19 Рис.19Равномерный белый шум Оценка математического ожидания (идентификатор mean_uniform) и дисперсии (идентификатор var_uniform) равномерного белого шума (идентификатор r_uniform) длины 10 000 с математическим ожидаем и дисперсией установленными по умолчанию. mean_uniform = 0.49956 var_uniform = 0.08291 График оценки автокорреляционной функции rx(m) шума (идентификатор r_r_uniform), центрированной относительно m = 0 (рис.20) 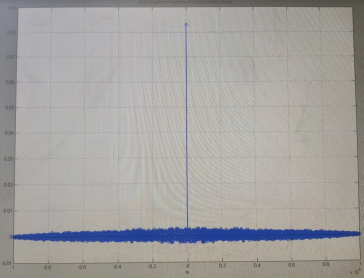 (Рис.20) Оценка математического ожидания (идентификатор mean_norm) и дисперсии (идентификатор var_norm) нормального белого шума (идентификатор r_uniform) длины 10 000 с математическим ожиданием и дисперсией, установленными по умолчанию. mean_norm = 0.0018848 var_norm = 0.97502 График оценки АКФ Rx(m) шума (идентификатор R_r_norm) центрированной относительно m = 0 (рис.21) 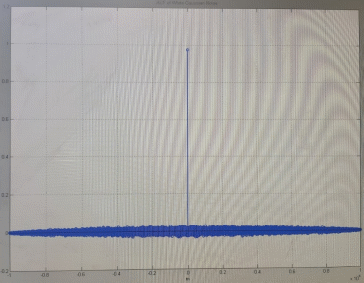 (Рис.21) Аддитивная смесь x8(n) (идентификатор x8) дискретного гармонического сигнала x(n) (2.12) с нормальным белым шумом и графиком на интервале времени (2.3) (рис.22) 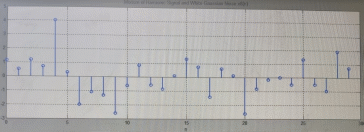 (Рис.22) (Рис.22)Оценка АКФ Rx(m) (идентификатор R) последовательности x8(n) и график АКФ, центрированной относительно m = 0. (рис.23) 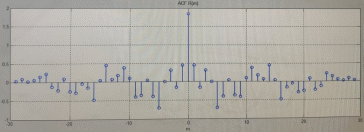 (Рис.23) (Рис.23)Оценка дисперсии последовательности x8(n) и значение Rx(m). var_x8 = 13.5194 R(N) = 13.4673 Нормальный белый шум с заданными статистическими характеристиками. Графики четырех разновидностей нормального белого шума длинны 10 000: С математическими ожидаем и дисперсией установленными по умолчанию, идентификатор шума r_norm (рис.24)  Рис.24 Рис.24С математическим ожиданием и дисперсией установленной по умолчанию, - идентификатор шума r_normMean (рис.25)  Рис.25 Рис.25С математическим ожиданием, установленным по умолчанию, и дисперсией var – идентификатор шума r_nornVar (рис.26)  Рис.26 Рис.26С математическим ожиданием mean и дисперсией var – идентификатор шума r_normMeanVar (рис.27)  Рис.27 График шумов в одинаковом диапозоне по оси ординат [-MAX MAX] с помощью функции ylim, где MAX равно максимальному значению шума среди четырех его разновидностей. Гистограммы четырех разновидностей нормального белого шума с помощью функции hist (параметры по умолчанию) (рис.28), (рис.29), (рис.30), (рис.31), : 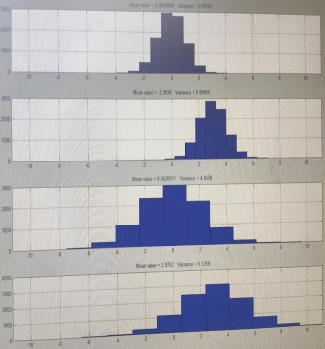 Рис.28 Рис.29 Рис.30 Рис.31 Гистограммы в одинаковом диапазоне по оси абсцисс [-MAX MAX] с помощью функции xlim, где значения MAX определённо раннее. В заголовке гистограмм выведены значения оценок математического ожидания (MeanValue) и дисперсии (Vanance) Контрольные вопросы Дайте определение дискретного и цифрового сигналов. Дискретным называют сигнал, дискретный по времени и непрерывный по состоянию (уровню). Цифровым называют сигнал, дискретный по времени и квантованный по уровню. Как математически описывается дискретный сигнал? Дискретный сигнал описывается последовательностью чисел бесконечной разности x(nT) или x(n), называемой короткой последовательностью. Какой тип данных используется по умолчанию при описании последовательностей в МАТLАВ? По умолчанию при описании последовательностей используется тип double. Что такое период и частота дискретизации и как они связаны друг с другом? При цифровой обработке сигналов осуществляют выборку значений аналогового сигнала через равные интервалы времени T. Данный процесс называется дискретизацией сигнала по времени. Время T называют периодом дискретизации, а величину обратно пропорциональную F=1/T – частотой дискретизации. Дайте определение дискретного нормированного времени. Значения nT называют дискретным временем (время n-ого отсчета), а n —дискретное нормированное время. Дайте определение нормированной частоты. Нормированная частота – абсолютная частота, нормированная к частоте дискретизации: 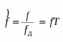 Нормированная круговая частота: 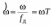 Какие дискретные сигналы называют детерминированными? Детерминированным дискретным сигналом называют сигнал, значения которого в любой момент времени заранее известны или могут быть определены точно по заданной математической модели. Назовите основные характеристики детерминированных дискретных сигналов Среднее значение, энергия, средняя мощность, автокорреляционная и автоковариационная функции. Поясните, с какой целью и как вычисляются автокорреляционная и автоковариационная функции. Автокорреляционная функция (АКФ2) Rx(m) последовательности длины N позволяет оценить зависимость между ее отсчетами при различных сдвигах по времени m. Автоковариационная функция rx(m) позволяет оценить зависимость между отклонениями отсчетов последовательности от среднего значения µx при различных сдвигах по времени m. Какими свойствами обладает АКФ? 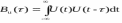 1) При 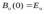 2) АКФ – функция чётная: 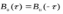 3) При любом значении временного сдвига 4) Обычно, АКФ представляется симметричной линей с центральным максимумом, который всегда положителен. При этом в зависимости от вида сигнала Какие дискретные сигналы называют случайными? Случайным (стохастическим) дискретным сигналом называют сигнал, значения которого в дискретные моменты времени заранее неизвестны и могут быть определены лишь с некоторой вероятностью. Что такое ансамбль реализаций случайного дискретного сигнала? Ансамблем реализаций называют совокупность случайных последовательностей xk(n), (строки матрицы X), а реализацией – одну из последовательностей. Назовите основные статистические характеристики случайных дискретных сигналов. Математическое ожидание, дисперсия, АКФ и автокореляционная функция. Как определяются основные статистические характеристики случайных дискретных сигналов по ансамблю реализаций? Посредством статистического усреднения. Какие случайные дискретные сигналы называют стационарными в широком смысле? Случайный дискретный сигнал X называют стационарным в широком смысле (стационарным по Хинчину), если его одномерная плотность вероятности не зависит от времени n, а двумерная –зависит только от сдвига по времени. Какие случайные дискретные сигналы называют эргодическими? Случайный дискретный сигнал называют эргодическим, если при определении его статистических характеристик усреднение по ансамблю реализаций эквивалентно усреднению по времени одной реализации, теоретически бесконечной длины N . Дайте определение равномерного белого шума и нормального белого шума. Равномерный белый шум – последовательность случайных чисел из диапазона [0; 1], распределенных по равномерному закону (математическое ожидание – 0,5 и дисперсия – 1/12) – с помощью функции: х = rand(l,N),где х – вектор-строка отсчетов случайной последовательности длины N. Нормальный белый шум – последовательность случайных чисел, распределенных по нормальному закону (математическое ожидание – 0 и дисперсия – 1) – с помощью функции: х = randn(l,N) Какой вид имеют АКФ нормального белого шума и автоковариационная функция равномерного белого шума? АКФ нормального и равномерного белого шума при N имеют вид цифрового единичного импульса. |