Лаб.раб. Интерполяция. Лабораторная работа 2 по теме Интерполяция функций Вопросы, подлежащие изучению

• Название: Лабораторная работа 2 по теме Интерполяция функций Вопросы, подлежащие изучению
• Дата: 19.02.2023
• Размер: 56.31 Kb.
• Имя файла: Лаб.раб. Интерполяция.docx
• Тип: Лабораторная работа; #945147

Лабораторная работа №2

по теме «Интерполяция функций»

1. Вопросы, подлежащие изучению

1. 
   Постановка задачи аппроксимации и интерполяции. Интерполяция в точке. Погрешность интерполяции.
   
2. 
   Основные понятия: интерполирующая и интерполируемая функции, условие интерполяции. Связь между числом узлов интерполяции и порядком интерполирующего полинома.
   
3. 
   Интерполяционный полином Лагранжа: назначение, область применения.
   
4. 
   Интерполяционная формула Ньютона, область применения.
   
5. 
   Конечные разности, их назначение и использование. Свойства конечных разностей
   
6. 
   Методика выбора узлов интерполяции при использовании формул Лагранжа и Ньютона.
   
7. 
   Способы оценки погрешностей интерполяции по формулам Лагранжа и Ньютона. Способы повышения точности интерполяции.
   

2. 
   Задание
   

В этой лабораторной работе решается задача интерполяции в точке путем построения семейства интерполяционных полиномов разных степеней с оценкой погрешности полученных решений.

1. 
   Выбрать из таблицы 1–1 индивидуальное задание для интерполяции:
   

• 
  точку интерполяции x=b для интерполяции полиномом Лагранжа;
  
• 
  точку интерполяции x=a для интерполяции полиномом Ньютона;
  

1. 
   Выполнить вручную интерполяцию в заданной точке x=b с использованием полинома Лагранжа 1–й, 2–й и 3–й степени:
   

• 
  выбрать из таблицы 1–2 с интерполируемой функцией четыре подходящих узла. Перенумеровать узлы и занести перенумерованные узлы в таблицы вида 1–3.
  
• 
  записать интерполяционные формулы для 1, 2 и 3-ей степени полинома;
  
• 
  выполнить расчеты по интерполяционным формулам для каждой степени полинома; все промежуточные вычисления производить с сохранением всех значащих цифр, окончательные результаты округлять до 4 знаков после десятичной точки.
  
• 
  занести полученные результаты в таблицу вида 1–4;
  
• 
  вычислить оценки погрешности в точке b для полиномов различных степеней и занести их в таблицу 1-4.
  

1. 
   Выполнить вручную интерполяцию в заданной точке x=a с использованием полинома Ньютона 1–й, 2–й и 3–й степени:
   

• 
  выбрать из таблицы 1–2 с интерполируемой функцией четыре подходящих узла. Перенумеровать узлы и занести перенумерованные узлы в таблицы вида 1–3.
  
• 
  заполнить таблицу конечных разностей (для интерполяционной формулы Ньютона);
  
• 
  записать интерполяционные формулы для 1, 2 и 3-ей степени полинома;
  
• 
  выполнить расчеты по интерполяционным формулам для каждой степени полинома; все промежуточные вычисления производить с сохранением всех значащих цифр, окончательные результаты округлять до 4 знаков после десятичной точки.
  
• 
  занести полученные результаты в таблицу вида 1–5;
  
• 
  вычислить оценки погрешности в точке а для полиномов различных степеней и занести их в таблицу 1-5.
  

4. 
   Объяснить полученные результаты и сделать выводы.
   

1.3. Варианты задания для ручного расчета и таблица интерполируемой функции

Таблица 1–1

№ варианта	Полином Ньютона x=a	Полином Лагранжа x=b
1	0.06	0.43
2	0.11	0.72
3	0.16	1.17
4	0.21	0.58
5	0.31	0.12
6	0.36	1.21
7	0.41	1.46
8	0.46	0.87
9	0.51	0.48
10	0.61	1.37
11	0.07	0.51
12	0.12	0.96
13	0.17	0.64
14	0.22	1.52
15	0.32	0.77
16	0.37	0.17
17	0.42	1.02
18	0.52	0.34
19	0.62	1.41
20	0.08	0.23
21	0.13	0.67
22	0.17	1.29
23	0.23	0.81
24	0.32	1.26
25	0.42	1.12
26	0.47	0.93
27	0.53	0.37
28	0.63	0.26
29	0.09	1.07
30	0.14	1.33

Таблица 1–2

№ узла	Значение аргумента xi	Значение функцииyi
0	0.05	-4.1710
1	0.10	-4.1330
2	0.15	-4.0845
3	0.20	-4.0240
4	0.25	-3.9500
5	0.30	-3.8610
6	0.35	-3.7555
7	0.40	-3.6320
8	0.45	-3.4890
9	0.50	-3.3250
10	0.55	-3.1385
11	0.60	-2.9280
12	0.65	-2.6920
13	0.70	-2.4290
14	0.75	-2.1375
15	0.80	-1.8160
16	0.85	-1.4630
17	0.90	-1.0770
18	0.95	-0.6565
19	1.00	-0.2000
20	1.05	0.2940
21	1.10	0.8270
22	1.15	1.4005
23	1.20	2.0160
24	1.25	2.6750
25	1.30	3.3790
26	1.35	4.1295
27	1.40	4.9280
28	1.45	5.7760
29	1.50	6.6750
30	1.55	7.6265

1.4. Формы таблиц для занесения результатов

Таблица 1–3

k	0	1	2	…	n
xk	x0	x1	x2	…	xn
yk	y0	y1	y2	…	yn

Таблица 1-4

(для полинома Лагранжа)

Степень многочлена k	Lk(x)	Погрешность
1	L1(x)	|L1(x) – L2(x)|
2	L2(x)	|L2(x) – L3(x)|
3	L3(x)	–

Таблица 1–5

(для полинома Ньютона)

Степень многочлена k	Pk(x)	Погрешность
1	P1(x)	|P1(x) – P2(x)|
2	P2(x)	|P2(x) – P3(x)|
3	P3(x)	–

1.5. Содержание отчета

1. Фамилия и имя студента, номер группы.

2. Название и цель лабораторной работы.

3. Индивидуальный вариант задания к работе.

4. Таблицы 1–3 с перенумерованными узлами интерполяции.

5. Интерполяционные формулы для ручных расчетов и результаты расчетов в таблицах 1–4 и 1-5.

6. Выводы.

1.6. Пример выполнения задания

1. 
   Точка интерполяции для формулы Лагранжа b = 0.52.
   

Выбор и перенумерация узлов.

Для ручной интерполяции в точке x = b = 0.52 по формуле Лагранжа выбираем из таблицы 1–2 4 узла так, чтобы точка b = 0.52 оказалась внутри получающийся таблицы и узлы были наиболее близкими к этой точке. В итоге выбираем узлы с номерами 8, 9, 10, 11:

8	0.45	-3.4890
9	0.50	-3.3250
10	0.55	-3.1385
11	0.60	-2.9280

Следует отметить, что формула Лагранжа может использоваться как для таблиц с постоянным шагом, так и с непостоянным шагом. Перенумеруем узлы интерполяции руководствуясь двумя правилами: точка x=b должна быть внутри таблицы и узлы должны быть ближайшие к ней. Занесем перенумерованные узлы в таблицу вида 1–3:

k	0	1	2	3
xk	0.50	0.55	0.45	0.60
yk	-3.3250	-3.1385	-3.4890	-2.9280

Ручной расчет по формуле Лагранжа.

Запишем интерполяционные полиномы Лагранжа 1–й, 2–й и 3–й степени и вычислим их значения в точке x = b = 0.52: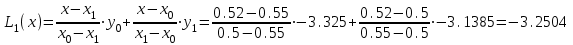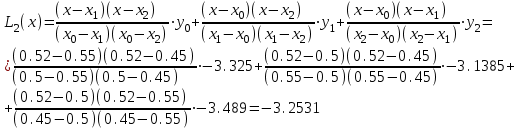





Обратите внимание, что: выражения для полиномов 1, 2 и 3 степени (в явном виде) после соответствующих преобразований следует получить самостоятельно!

Занесем результаты в таблицу и вычислим оценки погрешности полученных значений для многочленов 1–й и 2–й степени:

Степень многочлена k	Lk(x)	Оценка погрешности
1	–3.2504	0.0027
2	–3.2531	0.0001
3	–3.2532	–

Вывод. Получены выражения для интерполяционных полиномов 1, 2 и 3-ей степени и их значения в т. b. Оценку погрешности проведём в соответствии с неравенством:


Можно утверждать, что разность между точным (неизвестным) значением функции и значением интерполяционного полинома в точке x=0.52 после 3=х итераций не превышает 0.0001.

1. 
   Точка интерполяции для формулы Ньютона a = 0.12.
   

Выбор и нумерация узлов.

Для ручной интерполяции в точке x = a = 0.12 по 1 формуле Ньютона выбираем 4 узла из таблицы 1–2 так, чтобы точка a = 0.12 оказалась между узлами с номерами с 1 по 2 и добавляем узлы вправо:

Номера выбранных узлов (k)	xk	yk
1	0.10	-4.1330
2	0.15	-4.0845
3	0.20	-4.0240
4	0.25	-3.9500

Выбор точек определяется тем, чтобы при решении задачи интерполяции в точке по первой формуле Ньютона, точка должна быть внутри таблицы для полинома любой степени, в том числе и первой. Поэтому нулевой и первый узел должны находиться по разные стороны от самой точки x=a. Если нулевой узел находится слева от точки, а первый узел находится справа от точки, то шаг h=x1-x0 будет положительным и добавлять узлы следует справа относительно точки x=a. Если же нулевой узел находится справа от точки, а первый узел находится слева, то шаг h=x1-x0 будет отрицательным, и добавлять узлы следует слева.

Изменим нумерацию узлов интерполяции для использования их в интерполяционных формулах и занесем в таблицы вида 1–3.

k	0	1	2	3
xk	0.10	0.15	0.20	0.25
yk	-4.1330	-4.0845	-4.0240	-3.9500

Ручной расчет по 1–й формуле Ньютона.
Заполним таблицу конечных разностей:

x	y	Δy	Δ2y	Δ3y
0.10	-4.1330	0.0485	0.0120	0.0015
0.15	-4.0845	0.0605	0.0135
0.20	-4.0240	0.0740
0.25	-3.9500

Запишем 1–ю интерполяционную формулу Ньютона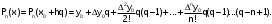



для полиномов 1–й, 2–й и 3–й степени и выполним расчеты по ним. Определим значение q: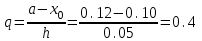



Значение полинома 1-й степени в т. x=0.12: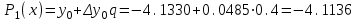


Значение полинома 2-й степени в т. x=0.12: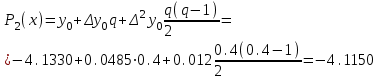



Значение полинома 3-й степени в т. x=0.12:
Важно: Явные выражения для полиномов 1, 2 и 3 степени могут быть получены после соответствующих преобразований формулы: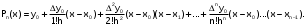


В нашем случае они будут иметь вид: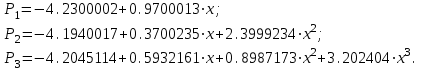


Занесем результаты в таблицу и вычислим оценки погрешности полученных значений для полиномов 1–й и 2–й степени:

Степень многочлена k	Pk(x)	Оценка погрешности
1	–4.1136	0.0014
2	–4.1150	0.0001
3	–4.1149	–

Вывод. Получены выражения для интерполяционных многочленов 1, 2 и 3-ей степени и их значения в точке а. Оценку погрешности проведём в соответствии с неравенством:



Можно утверждать, что разность между точным (неизвестным) значением функции и значением интерполяционного полинома в точке x=0.12 после 3-х итераций не превышает 0.0001.