эконометрика. ЭконометрикаЛабораторная2e. Лабораторная работа 2 Построение и анализ модели парной линейной регрессии Задание
 Скачать 241.16 Kb. Скачать 241.16 Kb.
|
Лабораторная работа № 2Построение и анализ модели парной линейной регрессииЗадание: Построить линейное уравнение парной регрессии y по x. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации. Оценить статистическую значимость уравнения парной регрессии в целом с помощью F-критерия Фишера (уровень значимости 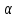 положить равным 0,05). положить равным 0,05).Оценить статистическую значимость параметров регрессии и корреляции с помощью t-критерия Стьюдента (уровень значимости 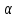 положить равным 0,05). положить равным 0,05).По всем полученным результатам сделать соответствующие выводы. Исходные данные: 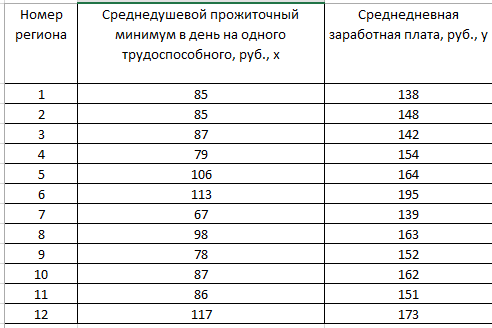 Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии 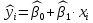 . .Для этого: а  ) выделим область пустых ячеек 52 ) выделим область пустых ячеек 52(5 строк, 2 столбца) для вывода результатов регрессионной статистики; б) активизируем Мастер функций в главном меню; в) в окне Категория выберем Статистические (рис.1), а в окне Функция – ЛИНЕЙН. Щелкнем по кнопке ОК; г) заполним аргументы функции (рис.2) Рис.1 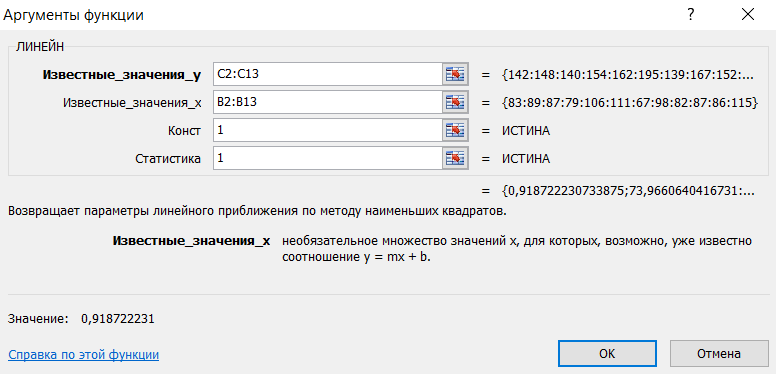 Рис.2 д  ) в левой верхней ячейке выделенной области появился первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмем на клавишу 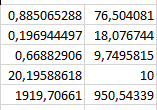 Рис.3 Рис.4 Получаем:
В результате получим оценочное уравнение линейной парной регрессии: 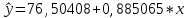 Величина коэффициента регрессии показывает, что при увеличении среднедушевого прожиточного минимума в день на одного трудоспособного среднедневная заработанная плата за месяц увеличивается на 885 рублей. Уравнение линейной регрессии дополняется выборочным парным линейным коэффициентом корреляции 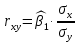 Показатель изменяется в пределах 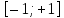 . Если . Если 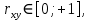 то связь между признаками прямая. Если то связь между признаками прямая. Если 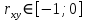 , то связь между признаками обратная. , то связь между признаками обратная.Для определения степени тесноты связи по значению линейного коэффициента корреляции используют шкалу Чеддока:  - практически отсутствует - практически отсутствует - слабая - слабая - умеренная - умеренная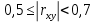 - заметная - заметная - сильная - сильная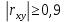 – тесная – теснаяВ нашем случае связь между  сильная, так как сильная, так как 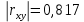 (рис.5). (рис.5).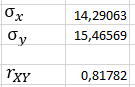 Рис.5 Если парный линейный коэффициент корреляции 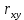 возвести в квадрат, то получим коэффициент детерминации возвести в квадрат, то получим коэффициент детерминации  . Данный коэффициент показывает, на сколько процентов вариация результативного признака объясняется вариацией факторного признака в общем объеме вариации. Получим коэффициент детерминации (рис.6): . Данный коэффициент показывает, на сколько процентов вариация результативного признака объясняется вариацией факторного признака в общем объеме вариации. Получим коэффициент детерминации (рис.6):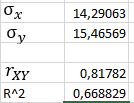 Рис.6 Вариация признака у на 66,882% объясняется вариацией признака х, остальные 33,118% приходятся на долю неучтенных в модели факторов. Оценим качество уравнения регрессии в целом с помощью F – критерия Фишера. Схема дисперсионного анализа имеет вид, представленный на рисунке 7 (n – число наблюдений, m – число параметров при переменной x).  Рис.7 Уравнение парной регрессии значимо с уровнем значимости α, если выполняется условие  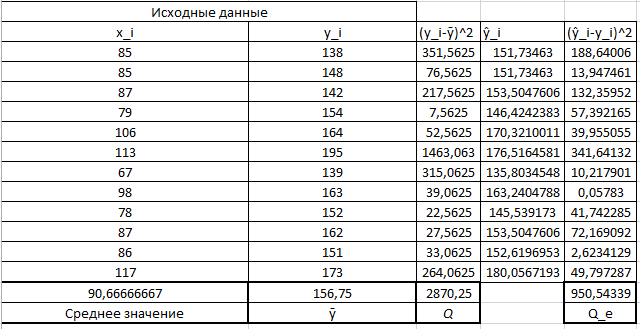 Q и Q_e вычисляются путём сложения ячеек выше Q_r Вычисляется по формуле: Подставляя в формулу вычисленные показатели получаем  При Сравнении с табличным значением понимаем, что уравнение значимо Проверка гипотезы Н0 о статистической незначимости коэффициентов регрессии и корреляции 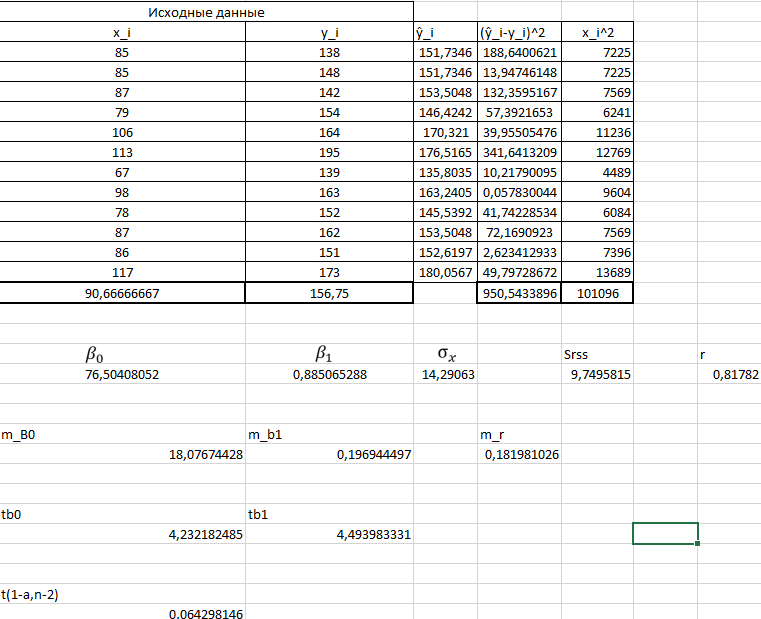 Стандартная ошибка коэффициента регрессии определяется по формуле:   Стандартная ошибка параметра a определяется по формуле:  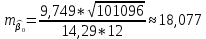 Величина стандартной ошибки совместно с t – распределением Стьюдента при n−2 степенях свободы применяется для проверки существенности коэффициента регрессии и параметра a, а также для расчета их доверительных интервалов. Для оценки существенности коэффициента регрессии и параметра a их величины сравниваются с их стандартными ошибками, т.е. определяются фактические значения t – критерия Стьюдента:  Затем они сравниваются с табличным значением при определенном уровне значимости α и числе степеней свободы n−2  Так как  и и  , то коэффициент регрессии β и параметр α статистически значимы. , то коэффициент регрессии β и параметр α статистически значимы. Вывод: между переменными X и Y есть линейная взаимосвязь в генеральной совокупности, статистическая значимость проверена с помощью t-критерия Стьюдента и F-критерия Фишера. Вариация признака у на 66,882% объясняется вариацией признака х, остальные 33,118% приходятся на долю неучтенных в модели факторов. При увеличении среднедушевого прожиточного минимума в день на одного трудоспособного среднедневная заработанная плата за месяц увеличивается на 885 рублей. |