лаба4. Лабораторная_работа_2_MATLAB (1). Лабораторная работа 2 Работа с матрицами в Matlab
 Скачать 379.5 Kb. Скачать 379.5 Kb.
|
|
Лабораторная работа 2 Работа с матрицами в Matlab Матрицы небольших размеров удобно вводить из командной строки. Существует три способа ввода матриц. Например, матрицу  можно ввести следующим образом: набрать в командной строке (разделяя элементы строки матрицы пробелами): A=[0.7 –2.5 9.1 и нажать <Enter>. Курсор перемещается в следующую строку (символ приглашения командной строки >> отсутствует). Элементы каждой следующей строки матрицы набираются через пробел, а ввод строки завершается нажатием на <Enter>. При вводе последней строки в конце ставится закрывающая квадратная скобка: >> A=[0.7 -2.5 9.1 8.4 0.3 1.7 -3.5 6.2 4.7] Если после закрывающей квадратной скобки не ставить точку с запятой для подавления вывода в командное окно, то матрица выведется в виде таблицы. Другой способ ввода матрицы основан на том, что матрицу можно рассматривать как вектор-столбец, каждый элемент которого является строкой матрицы. Поскольку точка с запятой используется для разделения элементов вектор-столбца, то ввод, к примеру, матрицы  осуществляется оператором присваивания: >> B=[6.1 0.3; -7.9 4.4; 2.5 -8.1]; Введите матрицу В и отобразите ее содержимое в командном окне, набрав в командной строке B и нажав <Enter>. Очевидно, что допустима такая трактовка матрицы, при которой она считается вектор-строкой, каждый элемент которой является столбцом матрицы. Следовательно, для ввода матрицы достаточно воспользоваться командой: >> C=[[0.4; 0.1] [-7.2; -2.1] [5.3; -9.5]] Обратите внимание, что внутренние квадратные скобки действительно нужны. Оператор C=[0.4; 0.1 -7.2; -2.1 5.3; -9.5] является недопустимым и приводит к сообщению об ошибке, поскольку оказывается, что в первой строке матрицы содержится только один элемент, во второй и третьей — по два, а в четвертой — снова один. Воспользуйтесь командой whos для получения информации о переменных A, B и C рабочей среды. В командное окно выводится таблица с информацией о размерах массивов, памяти, необходимой для хранения каждого из массивов, и типе — double array: >> whos A B C Name Size Bytes Class A 3x3 72 double array B 3x2 48 double array C 2x3 48 double array Функция size позволяет установить размеры массивов, она возвращает результат в виде вектора, первый элемент которого равен числу строк, а второй — столбцов: >> s=size(B) s = 3 2 Сложение и вычитание матриц одинаковых размеров производится с использованием знаков +, -. Звездочка * служит для вычисления матричного произведения, причем соответствующие размеры матриц должны совпадать, например: >> P=A*B P = 46.7700 -84.5000 53.1200 -9.9300 -58.5800 -11.8400 Допустимо умножение матрицы на число и числа на матрицу, при этом происходит умножение каждого элемента матрицы на число и результатом является матрица тех же размеров, что и исходная. Апостроф ' предназначен для транспонирования вещественной матрицы или нахождения сопряженной к комплексной матрице. Для возведения квадратной матрицы в степень применяется знак ^. Вычислите для тренировки матричное выражение >> R=(A-B*C)^3+A*B*C R = 1.0e+006 * -0.0454 0.1661 -0.6579 0.0812 -0.2770 1.2906 -0.0426 0.1274 -0.7871 MatLab обладает многообразием различных функций и способов для работы с матричными данными. Для обращение к элементу двумерного массива следует указать его строчный и столбцевой индексы в круглых скобках после имени массива, например: >> C(1,2) ans = -7.2000 Индексация двоеточием позволяет получить часть матрицы — строку, столбец или блок, например: >> c1=A(2:3,2) c1 = 0.3000 6.2000 >> r1=A(1,1:3) r1 = 0.7000 -2.5000 9.1000 Для обращения ко всей строке или всему столбцу не обязательно указывать через двоеточие начальный (первый) и конечный индексы, то есть операторы r1=A(1,1:3) и r1=A(1,:) эквивалентны. Для доступа к элементам строки или столбца от заданного до последнего можно использовать end, так же как и для векторов: A(1,2:end). Выделение блока, состоящего из нескольких строк и столбцов, требует индексации двоеточием как по первому измерению, так и по второму. Пусть в массиве T хранится матрица: 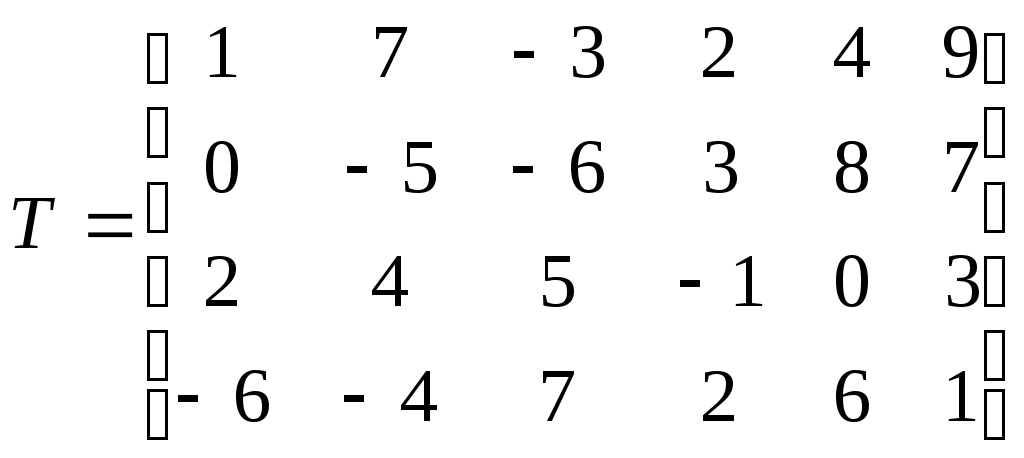 Для выделения ее элементов (обозначенных курсивом) со второй строки по третью и со второго столбца по четвертый, достаточно использовать оператор: >> T1=T(2:3,2:4) T1 = -5 -6 3 4 5 -1 Индексация двоеточием так же очень полезна при различных перестановках в массивах. В частности, для перестановки первой и последней строк в произвольной матрице, хранящейся в массиве A, подойдет последовательность команд: >> s=A(1,:); >> A(1,:)=A(end,:); >> A(end,:)=s; MatLab поддерживает такую операцию, как вычеркивание строк или столбцов из матрицы. Достаточно удаляемому блоку присвоить пустой массив, задаваемый квадратными скобками. Например, вычеркивание второй и третьей строки из массива T, введенного выше, производится следующей командой: >> T(2:3,:)=[] T = 1 7 -3 2 4 9 -6 -4 7 2 6 1 Индексация двоеточием упрощает заполнение матриц, имеющих определенную структуру. Предположим, что требуется создать матрицу  Первый шаг состоит в определении нулевой матрицы размера пять на пять, затем заполняются первая и последняя строки и первый и последний столбцы: >> W(1:5,1:5)=0; >> W(1,:)=1; >> W(end,:)=1; >> W(:,1)=1; >> W(:,end)=1; Проверьте, что в результате получается требуемая матрица. Ряд встроенных функций, приведенных в таблице 1, позволяет ввести стандартные матрицы заданных размеров. Обратите внимание, что во всех функциях, кроме diag, допустимо указывать размеры матрицы следующими способами: числами через запятую (в двух входных аргументах); одним числом, результат — квадратная матрица; вектором из двух элементов, равных числу строк и столбцов. Последний вариант очень удобен, когда требуется создать стандартную матрицу тех же размеров, что и некоторая имеющаяся матрица. Если, к примеру, A была определена ранее, то команда I=eye(size(A)) приводит к появлению единичной матрицы, размеры которой совпадают с размерами A, так как функция size возвращает размеры матрицы в векторе. Разберем, как получить трехдиагональную матрицу размера семь на семь, приведенную ниже, с использованием функций MatLab. 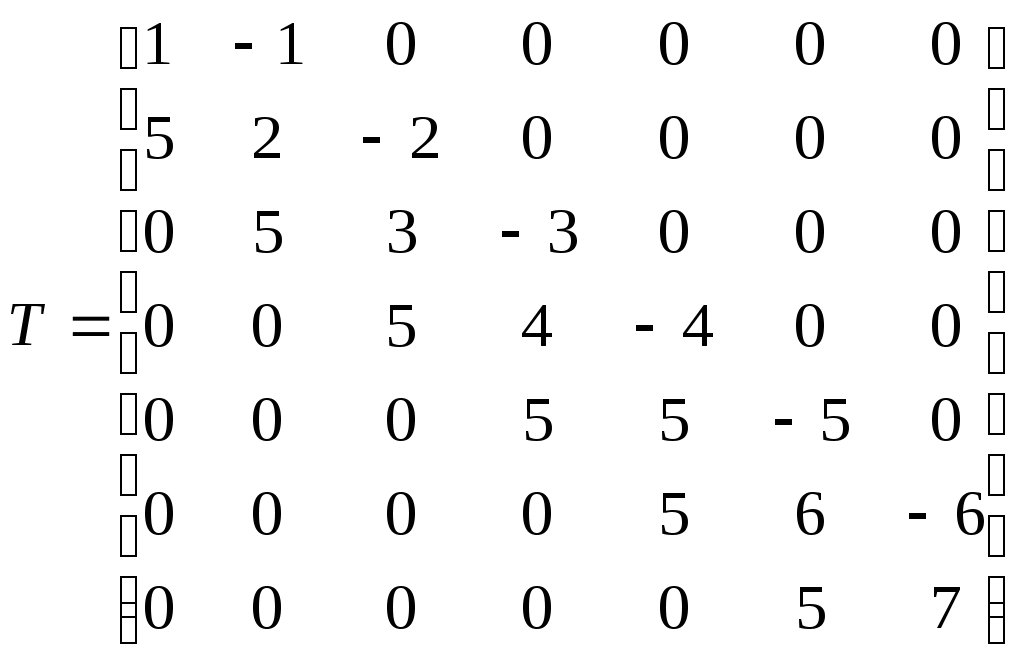 Введите вектор v с целыми числами от одного до семи v=[1 2 3 4 5 6 7] и используйте его для создания диагональной матрицы и матрицы со смещенной на единицу вверх диагональю. Вектор длины шесть, содержащий пятерки, заполняется, например, так: 5*ones(1,6). Этот вектор укажите в первом аргументе функции diag, а минус единицу — во втором и получите третью вспомогательную матрицу. Теперь достаточно вычесть из первой матрицы вторую и сложить с третьей: >> T=diag(v)-diag(v(1:6),1)+diag(5*ones(1,6),-1) Таблица 1 Функции для создания стандартных матриц
В предыдущем параграфе было описано применение поэлементных операций к векторам. Поэлементные вычисления с матрицами производятся практически аналогично, разумеется, необходимо следить за совпадением размеров матриц: A.*B, A./B— поэлементные умножение и деление; A.^p — поэлементное возведение в степень, p — число; A.^B — возведение элементов матрицы A в степени, равные соответствующим элементам матрицы B; A.' — транспонирование матрицы (для вещественных матриц A' и A.' приводят к одинаковым результатам); Иногда требуется не просто транспонировать матрицу, но и "развернуть" ее. Разворот матрицы на 90o против часовой стрелки осуществляет функция rot90: >> Q=[1 2;3 4] Q = 1 2 3 4 >> R=rot90(Q) R = 2 4 1 3 Допустимо записывать сумму и разность матрицы и числа, при этом сложение или вычитание применяется, соответственно, ко всем элементам матрицы. Вызов математической функции от матрицы приводит к матрице того же размера, на соответствующих позициях которой стоят значения функции от элементов исходной матрицы. В MatLab определены и матричные функции, например, sqrtm предназначена для вычисления квадратного корня. Найдите квадратный корень из матрицы и проверьте полученный результат, возведя его в квадрат (по правилу матричного умножения, а не поэлементно!): >> K=[3 2; 1 4]; >> S=sqrtm(K) S = 1.6882 0.5479 0.2740 1.9621 >> S*S ans = 3.0000 2.0000 1.0000 4.0000 Матричная экспонента вычисляется с использованием expm. Специальная функция funm служит для вычисления произвольной матричной функции. Все функции обработки данных могут быть применены и к двумерным массивам. Основное отличие от обработки векторных данных состоит в том, что эти функции работают с двумерными массивами по столбцам, например, функция sum суммирует элементы каждого из столбцов и возвращает вектор-строку, длина которой равна числу столбцов исходной матрицы: >> M=[1 2 3; 4 5 6; 7 8 9] M = 1 2 3 4 5 6 7 8 9 >> s=sum(M) s = 12 15 18 Если в качестве второго входного аргумента sum указать 2, то суммирование произойдет по строкам. Для вычисления суммы всех элементов матрицы требуется дважды применить sum: >> s=sum(sum(M)) s = 45 Очень удобной возможностью MatLab является конструирование матрицы из матриц меньших размеров. Пусть заданы матрицы:  , , 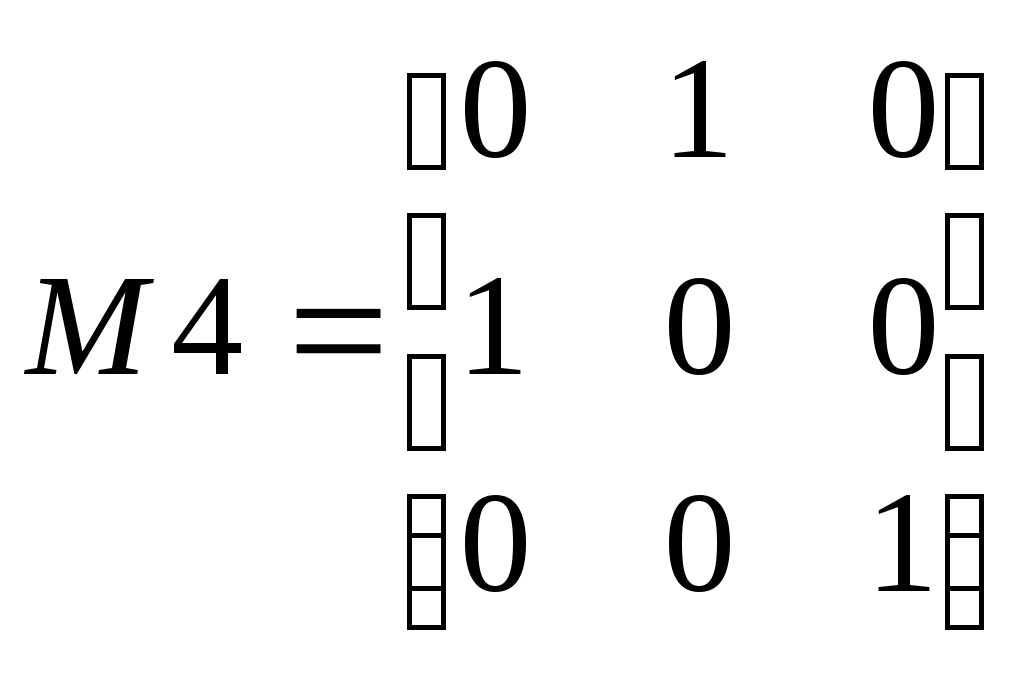 Требуется составить из М1, М2, М3 и М4 блочную матрицу М Можно считать, что М имеет размеры два на два, а каждый элемент является, соответственно, матрицей М1, М2, М3 или М4. Следовательно, для получения в рабочей среде MatLab массива M с матрицей М требуется использовать оператор: >> M=[M1 M2; M3 M4] Программирование в MatLab Язык программирования MatLab достаточное простой, он содержит основной набор конструкций: операторы ветвления и циклы. Простота языка программирования окупается огромным количеством встроенных функций, которые позволяют решать задачи из различных областей. Цикл for используется для повторения операторов в случае, когда число повторений заранее известно. В цикле for используется счетчик цикла, его начальное значение, шаг и конечное значение указываются через двоеточие. Блок операторов, размещенный внутри цикла, должен заканчиваться словом end. Листинг 1 содержит файл-программу для вывода графиков функции |
