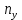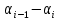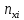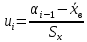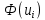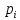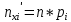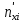Математика, ЛР, теория вероятности. ЛР 2. Лабораторная работа 2 Статистическая проверка гипотезы о нормальном распределении признака x генеральной совокупности (X,Y). Отчёт
 Скачать 58.53 Kb. Скачать 58.53 Kb.
|
|
Министерство науки и образование Российской Федерации ФГАОУ ВО «Уральский федеральный университет имени первого президента России Б.Н. Ельцина» Кафедра вычислительных методов и уравнений математической физики Оценка работы________ ЛАБОРАТОРНАЯ РАБОТА № 2 Статистическая проверка гипотезы о нормальном распределении признака X генеральной совокупности (X,Y). Отчёт Преподаватель________________________ Студент______________________________ Группа_______ Екатеринбург УрФУ 2022 Цель работы: проверить по критерию Пирсона согласуется ли гипотеза о нормальном распределении одного из признаков генеральной совокупности при уровне значимости 0,05. Если нет, то определить уровень значимости, при котором гипотезу о нормальном распределении можно принять. Найти интервальные оценки параметров a и с доверительной вероятностью 1 . Вариант 1 Таблица 1
 Проверим гипотезу 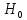 о нормальном распределении X по критерию Пирсона и найдем интервальные оценки a и . о нормальном распределении X по критерию Пирсона и найдем интервальные оценки a и .Объединим первый и второй, седьмой и шестой интервалы, так как значения частоты в в первом и седьмом меньше 5(см. табл. 1) Для вычисления по данным выборки значений статистики 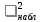 составим расчетную таблицу 2 составим расчетную таблицу 2
При расчетах использовались значения, полученные в лабораторной работе №1: 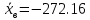 ; ; 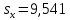 ; n=93 ; n=93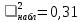 ; число интервалов ; число интервалов 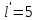 , r=2; число степей свободы , r=2; число степей свободы 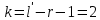 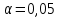 . . 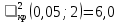 ; ; 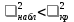 , Следовательно гипотезу , Следовательно гипотезу 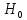 отвергать не следует. отвергать не следует.Доверительный интервал для неизвестного математического ожидания a, при: 1 1 0,05 0,95, n=93, 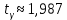 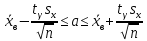 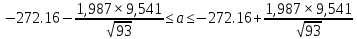 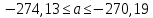 Доверительный интервал для неизвестной дисперсии при 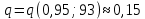 sx1 q sx1 q 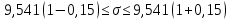 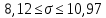 Для признака X плотность нормального распределения: 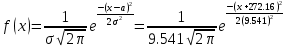 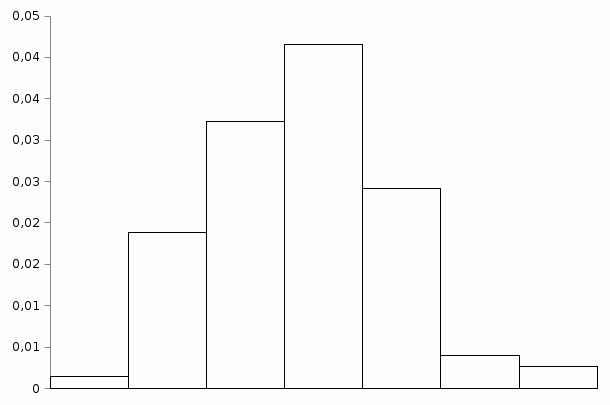 Рис 1. Гистограмма относительных частот 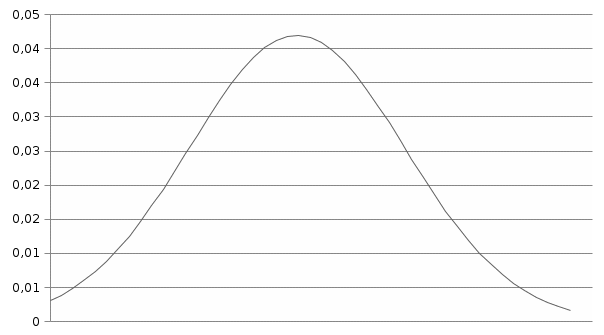 Рис 2. Функция плотности относительных частот |