Лабораторная работа 2 студент 3го курса направление 11. 03. 02 студ билет 7бин18013 Мардинская Ю. В
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
Кафедра инфокоммуникационных и общепрофессиональных дисциплин Дисциплина: Общая теория связи Лабораторная работа №2 Выполнил:студент 3-го курсанаправление 11.03.02 студ. билет №7БИН18013 Мардинская Ю.В. Преподаватель:Чернявский А.Д. Нижний Новгород 2021 Теоретическая часть Цель работы: с помощью программы Micro-Cap получить дискретные спектры различных импульсных сигналов с использованием аппарата дискретного преобразования Фурье (ДПФ). В настоящее время большое значение придается цифровой обработке сигналов (ЦОС). На практике вычисление спектральной плотности происходит с помощью цифровых вычислительных машин (рис. 8). 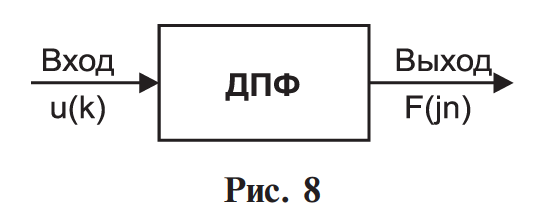 Поэтому сигнал представляют в виде конечного числа дискретных отсчетов. Пусть сигнал представлен последовательностью из N отсчетов u(k), 0 < k < N — 1. Дёя того, чтобы из непрерывного сигнал u(t) получить отсчеты, нужно положить t = kT, где Т — интервал дискретизации во временной области (обычно эта величина постоянная и выбирается так, чтобы выполнялась теорема Котельникова); k = 0, 1, ..., N — 1 — целые числа. Прямым дискретным преобразованием Фурье называют последовательность вида 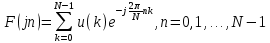 Обратным дискретным преобразованием Фурье называют последовательность вида 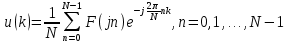 Определенные выше преобразования Фурье, не являются единственно возможными. На практике применяют и альтернативные преобразования Фурье. Пример. Рассчитаем ДПФ дискретного периодического сигнала, заданного на интервале своей периодичности шестью равноотстоящими отсчетами (N=6) u(k) = {1, 1, 1, 0, 0, 0}. Этот дискретный сигнал (рис. 9) можно выразить с помощью следующей формулы u(k) = 1, k = 0; 1, k = 1; 1, k=2; 0, k  3 3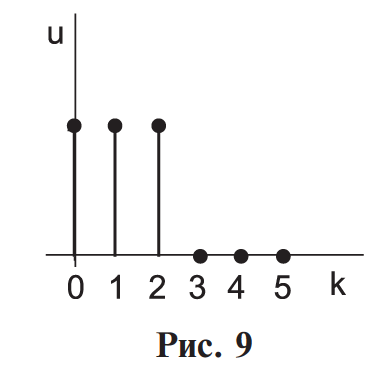 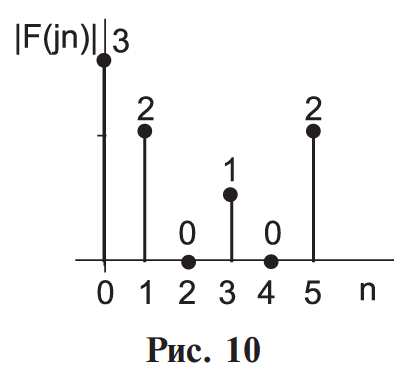 В табл. 1 приведены результаты расчета ДПФ и его модуля 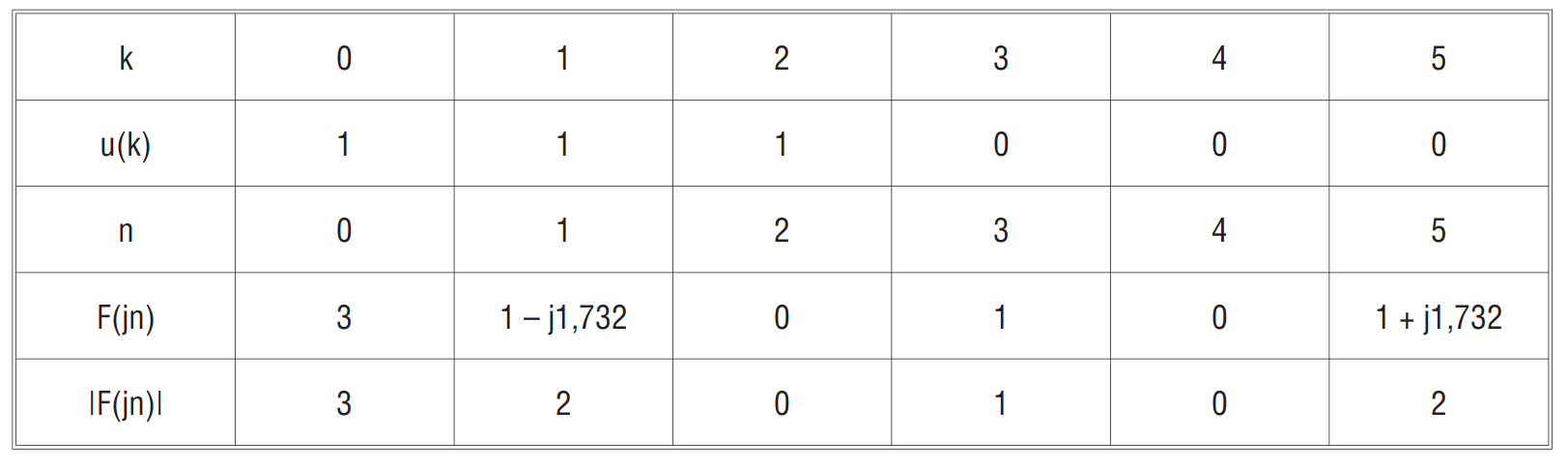 Практическая часть Найти непрерывную спектральную плотность 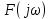 прямоугольного импульса (рис. 1) прямоугольного импульса (рис. 1)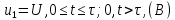 где t — время; 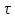 = 1 мс — длительность импульса; = 1 мс — длительность импульса;U = 4 В — амплитуда импульса. В формате Micro-Cap эта формула записывается так: VALUME = 4*(t< = 1m) Если неравенство в скобках истинно, то четверка умножается на 1. Если t таково, что неравенство в скобках ложно. то четверка умножается на 0. Построить график модуля непрерывной спектральной плотности как функцию от частоты | 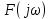 |. |.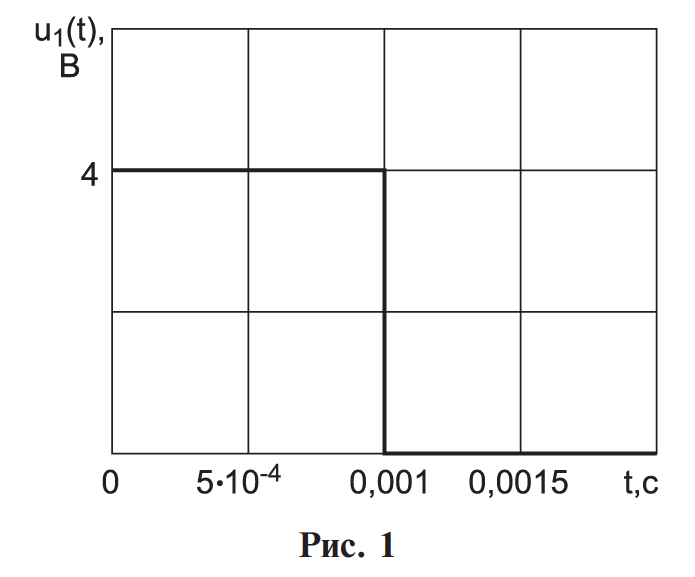 Так как сигнал представляет собой непериодическую функцию времени, найдем спектральную функцию импульса u1(t) на основании интегрального преобразования Фурье. Согласно области определения сигнал отличен от нуля при tϵ[0, 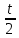 ], интегральное преобразование Фурье, будет иметь следующий вид: ], интегральное преобразование Фурье, будет иметь следующий вид: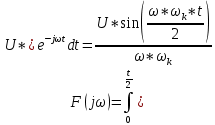 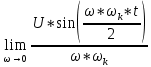 В данном случае значение предела будет 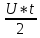 , это значение спектральной функции при ωk=0. Модуль непрерывной спектральной плотности как функцию от частоты | , это значение спектральной функции при ωk=0. Модуль непрерывной спектральной плотности как функцию от частоты | |, будет: |, будет: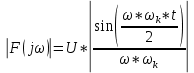 Так как 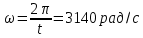 , то: , то:
Найти непрерывную спектральную плотность 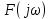 серии из трех прямоугольных импульсов показанных на рис. 2. серии из трех прямоугольных импульсов показанных на рис. 2.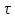 = 0,1 мс — длительность импульса; = 0,1 мс — длительность импульса;Т = 0,4 мс — период; U = 1 В — амплитуда импульса. Построить график модуля непрерывной спектральной плотности как функцию от частоты | 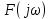 |. |.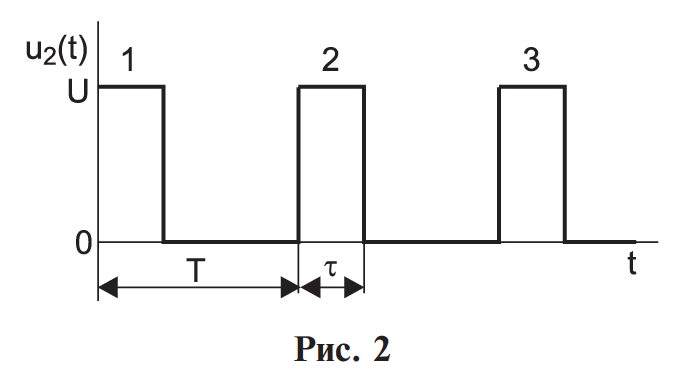 Построим график модуля непрерывной спектральной плотности как функцию от частоты | 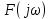 |. |.Сигнал отличен от нуля на интервалах t: [0, 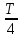 ], [ ], [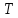 , ,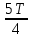 ], [ ], [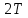 , ,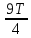 ], следовательно, интеграл фурье будет иметь следующий вид: ], следовательно, интеграл фурье будет иметь следующий вид: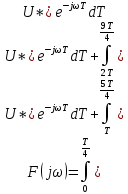 Воспользовавшись алгоритмом расчета предыдущей задачи получаем: 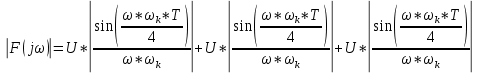 Принимая во внимание что 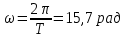 , расчетную часть произведем в Excel. , расчетную часть произведем в Excel.
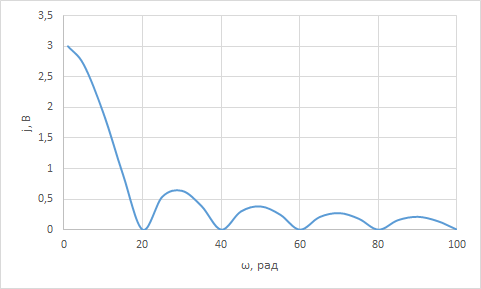 Найти непрерывную спектральную плотность 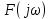 затухающей синусоиды (рис. 3) затухающей синусоиды (рис. 3)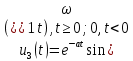 . .где t — время; a = 800 1/с — коэффициент; 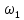 = 8000 рад/c — угловая частота. = 8000 рад/c — угловая частота.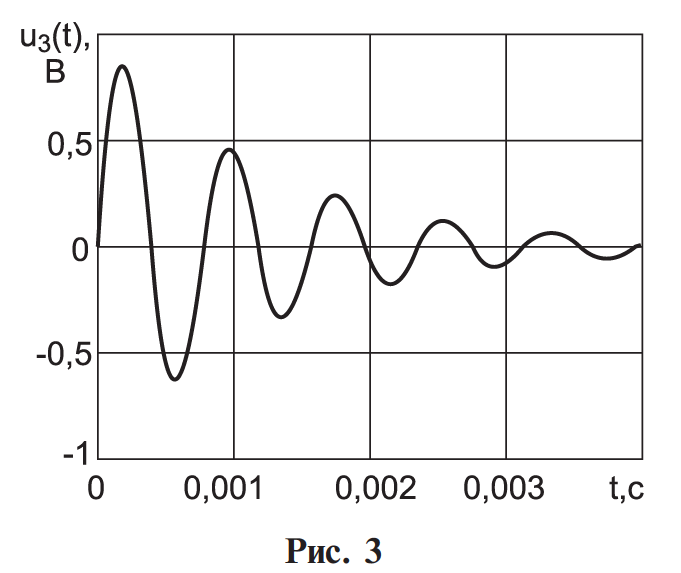 Построить график модуля непрерывной спектральной плотности как функцию от частоты | 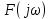 |. |.Так как модуль спектра экспотенциального импульса: 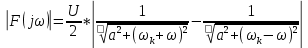 А амплитуда напряжения (U) согласно графику, на рисунке 6 составляет 1 В., то проведя расчет на интервале ωkϵ[0,12000] рад, получаем:
По данным таблицы график модуля непрерывной спектральной плотности имеет следующий вид: 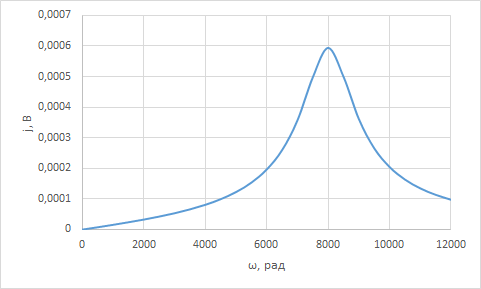 Найти непрерывную спектральную плотность 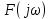 прямоугольного радиоимпульса, образованного отрезком синусоиды (рис. 4). прямоугольного радиоимпульса, образованного отрезком синусоиды (рис. 4).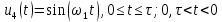 где 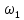 = 8000 рад/с — угловая частота; = 8000 рад/с — угловая частота;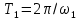 — период синусоиды; — период синусоиды;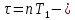 — длительность импульса; — длительность импульса;n = 3 — целое число периодов за время 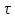 . .Построить график модуля непрерывной спектральной плотности как функцию от частоты |F(j 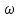 |. |.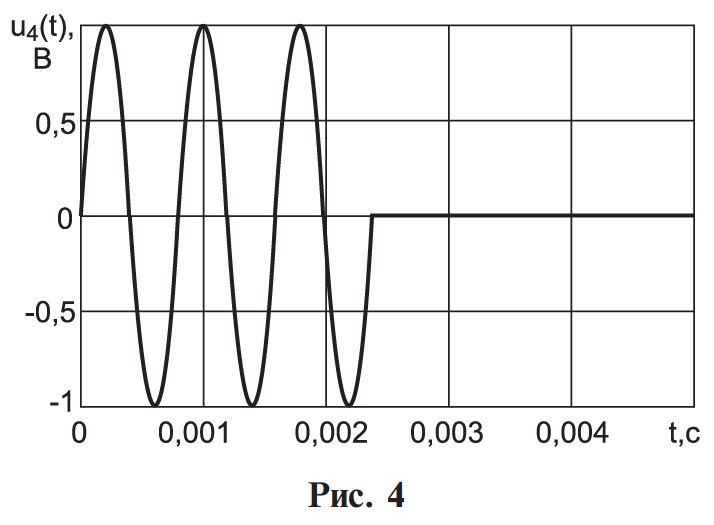 Так как 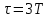 , то , то 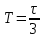 Интегральное преобразование фурье для данной задачи, выглядит следующим образом: 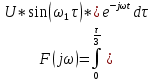 Представим подынтегральное выражение в экспоненциальной форме. Согласно формуле Эйлера, имеем: 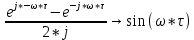 Тогда интеграл приводится к виду: 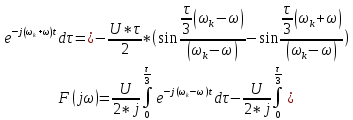 Тогда: 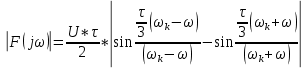 Стоит отметить что при ωk=ω=8000 рад, 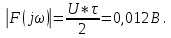 произведем расчет на интервале ωkϵ[0,2ω] рад: произведем расчет на интервале ωkϵ[0,2ω] рад:
По данным таблицы график модуля непрерывной спектральной плотности имеет следующий вид: 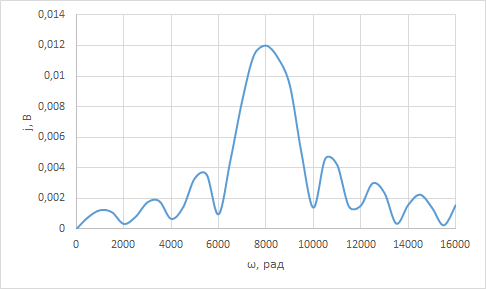 Найти непрерывную спектральную плотность F(j 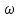 ) серии из трех прямоугольных радиоимпульсов (из трех отрезков синусоид), показанных на рис. 5. ) серии из трех прямоугольных радиоимпульсов (из трех отрезков синусоид), показанных на рис. 5.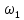 = 8000 рад/с — угловая частота; = 8000 рад/с — угловая частота;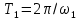 — период синусоиды; — период синусоиды;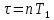 — длительность импульса; — длительность импульса;n = 3 — целое число периодов за время 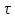 ; ;T=4 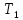 — период. — период.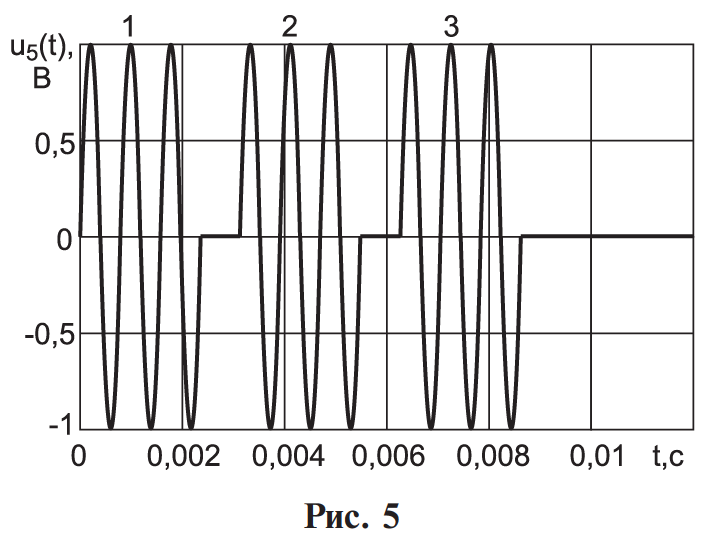 Построить график модуля непрерывной спектральной плотности как функцию от частоты |F(j 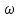 )|. )|.Поскольку, как и в предыдущей задаче период синусойды 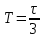 , и согласно графику на рисунке 8, сигнал существует на интервалах: [0, , и согласно графику на рисунке 8, сигнал существует на интервалах: [0,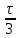 ], [ ], [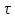 , ,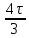 ], [ ], [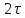 , ,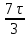 ], во всех остальных случаях сигнал нулевой. ], во всех остальных случаях сигнал нулевой.Интегральное преобразование фурье для данной задачи, выглядит следующим образом: 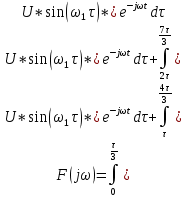 Воспользовавшись расчетами из предыдущей задачи получим: 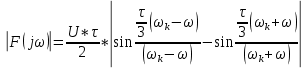 + +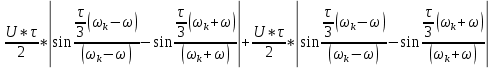 Стоит отметить что, как и в предыдущей задаче, при ωk=ω=8000 рад, 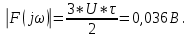 произведем расчет на интервале ωkϵ[0,2ω] рад: произведем расчет на интервале ωkϵ[0,2ω] рад:
По данным таблицы график модуля непрерывной спектральной плотности имеет следующий вид: 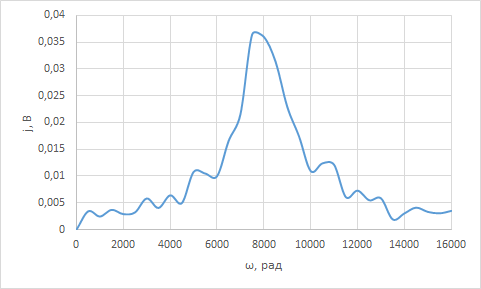 Практическая часть ДПФ прямоугольного импульса Для осуществления исследования в среде MicroCap 11 построим схему содержапщий функциональный источник сигнала E1. Для простроения ДПФ прямоугольного импульса 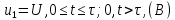 , со следующими параметрами: , со следующими параметрами:τ = 1 мс — длительность импульса; U = 4 В — амплитуда импульса. В окне VALUE источника Е1 введем формулу 4*(t<1m). Схема исследуемой цепи будит иметь следующий вид:  График ДПФ прямоугольного импульса, простроенный в среде MicroCap 11 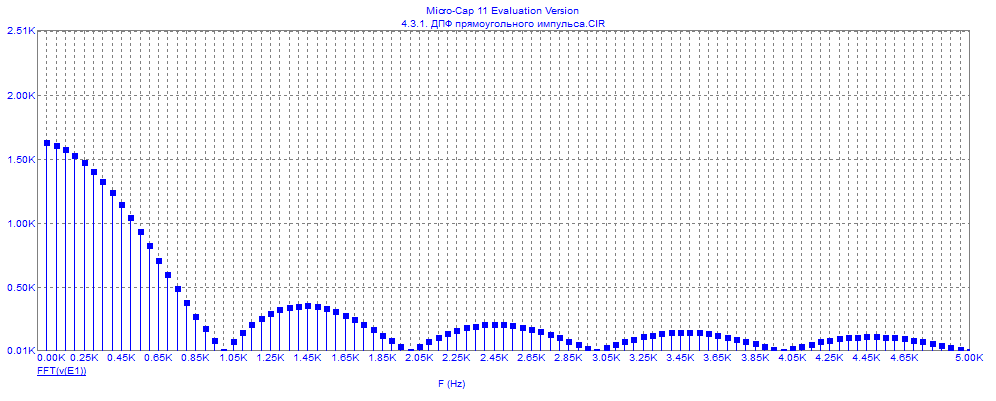 ДПФ для трех прямоугольных импульсов Для данного исследования изменим формулу сигнала источника Е1. Так как сигнал имеет следующие характеристики: τ = 0,1 мс — длительность импульса; Т = 0,4 мс — период; U = 1 В — амплитуда импульса. То, в окне VALUE, источника E1, вместо 4*(t<1m) введем формулу для трех прямоугольных импульсов: 1*(t>=0)-1*(t> = 0.1m)+1*(t> = 0.4m)-1*(t> = 0.5m)+1*(t> = 0.8m)-1*(t> = 0.9m). 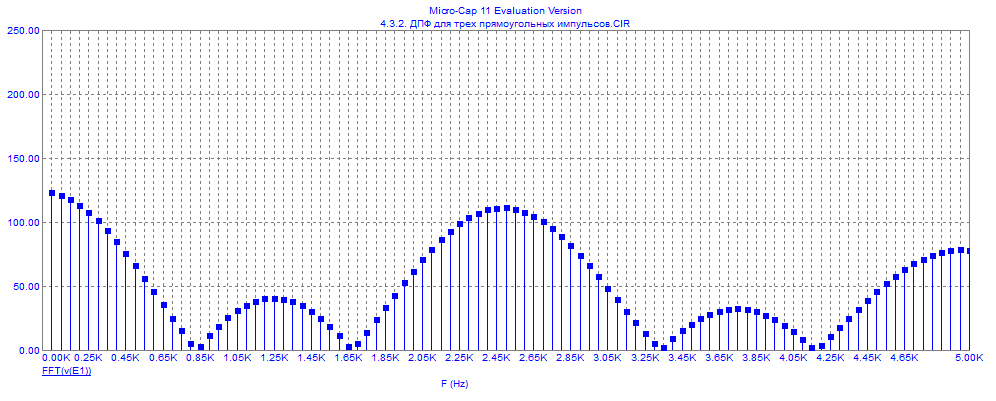 ДПФ для затухающей синусоиды В данном случае исследуемый сигнал 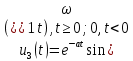 имеет следующие характеристики: имеет следующие характеристики:t — время; a = 800 1/с — коэффициент; 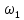 = 8000 рад/c — угловая частота. = 8000 рад/c — угловая частота.Для построения его ДПФ вновь изменим Е1 VALUE введя формулу для затухающей синусоиды: exp(-800*t)*sin(8000*t). График ДПФ для затухающей синусоиды, простроенный в среде MicroCap 11, будет иметь следующий вид:  ДПФ для отрезка синусоиды В данном случае исследуется сигнал  , ,где:  = 8000 рад/с — угловая частота; = 8000 рад/с — угловая частота;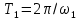 — период синусоиды; — период синусоиды;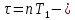 — длительность импульса; — длительность импульса;n = 3 — целое число периодов за время 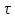 Поэтому вернемся к исходной схеме, и вновь изменим формулу сигнала Е1. В окне VALUE введем формулу отрезка синусоиды: sin(8000*t)*(t> = 0)-sin(8000*t)*(t> = 2.356m). 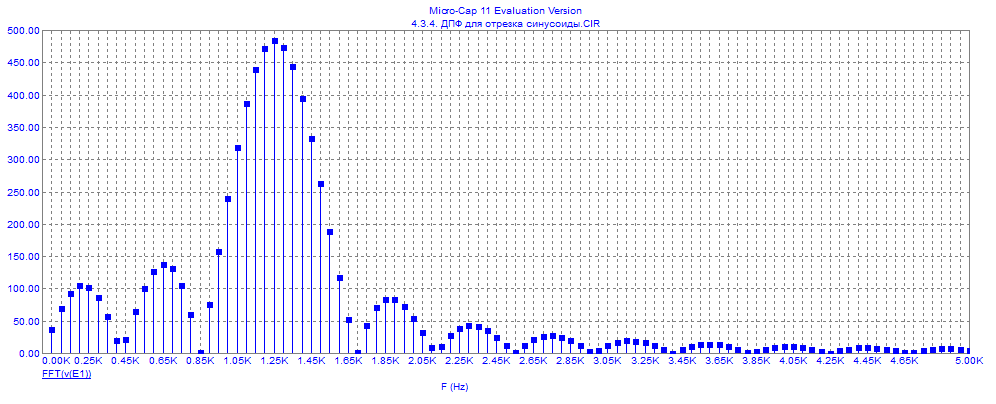 ДПФ для серии радиоимпульсов Построим график ДПФ (FFT) для сигнала из серии трех прямоугольных радиоимпульсов, со следующими характеристиками: 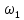 = 8000 рад/с — угловая частота; = 8000 рад/с — угловая частота;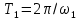 — период синусоиды; — период синусоиды;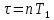 — длительность импульса; — длительность импульса;n = 3 — целое число периодов за время 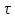 ; ;T=4 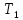 — период. — период.Для этого, вновь изменим Е1 VALUE на формулу для трех отрезков синусоиды: sin(8000*t)*(t> = 0)-sin(8000*t)*(t> = 2.356m)+sin(8000*t)*(t> = 3.142m)-sin(8000*t)*(t> = 5.498m)+sin(8000*t)*(t> = 6.283m)-sin(8000*t)*(t> = 8.639m). 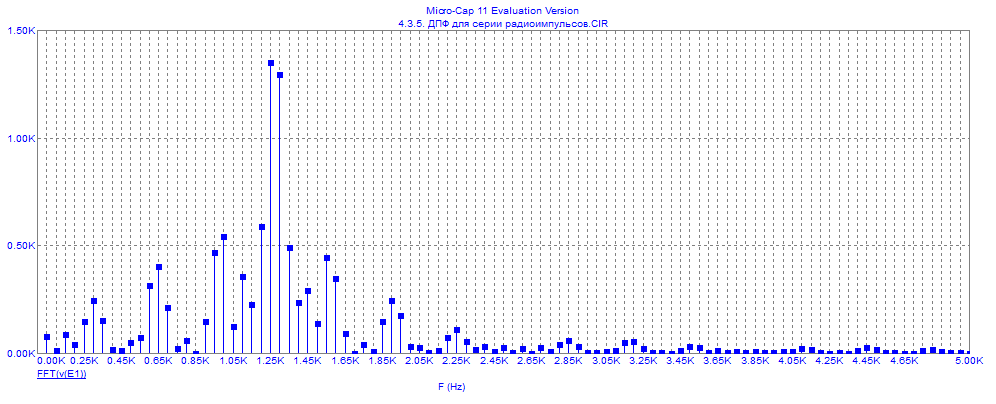 |

