Лабораторная работа 2 Транспортная задача Вариант 15 Проверил преподаватель студент гр. Псгв319 Ие О. Н. Осипов Н. В

• Название: Лабораторная работа 2 Транспортная задача Вариант 15 Проверил преподаватель студент гр. Псгв319 Ие О. Н. Осипов Н. В
• Дата: 10.04.2022
• Размер: 172.22 Kb.
• Имя файла: LR2.docx
• Тип: Лабораторная работа; #459233

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Федеральное государственное бюджетное образовательное учреждение

высшего образования

"Уральский государственный университет путей сообщения"

(ФГБОУ ВО УрГУПС)

Кафедра «Естественнонаучные дисциплины»

Лабораторная работа №2

«Транспортная задача»

Вариант 15

Проверил: Выполнил:

преподаватель студент гр. ПСгв-319

Ие О.Н. Осипов Н.В.

Екатеринбург

2022

Задание 1

На станциях 𝐴_𝑖 (𝑖 = 1, 2, 3, 4) сосредоточен однородный груз в количестве 𝑎_𝑖 единиц груза, который требуется перевезти на станции назначения 𝐵_𝑗 (𝑗 = 1, 2, 3, 4, 5) в соответствии с потребностями каждой станции в 𝑏_𝑗 единиц груза. Известны затраты 𝑐_𝑖𝑗 на перевозку единицы груза с любой станции 𝐴_𝑖 на любую станцию 𝐵_𝑗. Требуется составить такой план перевозок, чтобы весь груз был вывезен, все потребности были бы удовлетворены, а суммарные затраты были бы минимальны. Исходные данные приведены в таблице.

1. Используя методы северо-западного угла, наименьшей стоимости, двойного предпочтения, найти три различных опорных плана и вычислить стоимости перевозок. Выбрать лучший из них (с меньшим значением целевой функции).

2. Перейти к оптимальному плану, применив метод потенциалов.

3. Выполнить проверку нахождения оптимального плана в пакете Excel.

4. Выполнить проверку нахождения оптимального плана в пакете Mathcad.

Решение

Метод северо-западного угла

Проверим необходимое и достаточное условие разрешимости задачи:

∑a = 15 + 10 + 24 = 49;

∑b = 20 + 12 + 37 = 69.

Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу с запасом груза, равным 20 (49-69). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю.

Занесем исходные данные в распределительную таблицу.

		B1	B2	B3
	ai \ bj	20	12	37
A1	15	5| 15	3|	7|
A2	10	3| 5	2| 5	3|
A3	24	6|	4| 7	8| 17
A4	20	0|	0|	0| 20

Вычислим суммарную стоимость перевозок: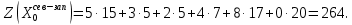



Метод наименьшей стоимости

Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j.

Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку, и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.

Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

Искомый элемент равен c₂₂=2. Для этого элемента запасы равны 10, потребности 12. Поскольку минимальным является 10, то вычитаем его.

x₂₂ = min(10,12) = 10.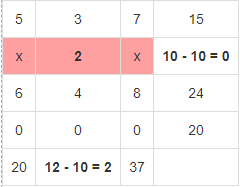



Искомый элемент равен c₁₂=3. Для этого элемента запасы равны 15, потребности 2. Поскольку минимальным является 2, то вычитаем его.

x₁₂ = min(15,2) = 2.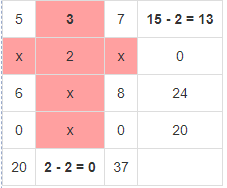



Искомый элемент равен c₁₁=5. Для этого элемента запасы равны 13, потребности 20. Поскольку минимальным является 13, то вычитаем его.

x₁₁ = min(13,20) = 13.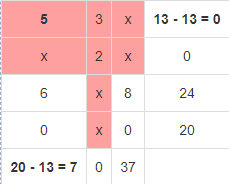



Искомый элемент равен c₃₁=6. Для этого элемента запасы равны 24, потребности 7. Поскольку минимальным является 7, то вычитаем его.

x₃₁ = min(24,7) = 7.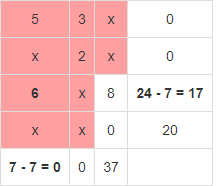



Искомый элемент равен c₃₃=8. Для этого элемента запасы равны 17, потребности 37. Поскольку минимальным является 17, то вычитаем его.

x₃₃ = min(17,37) = 17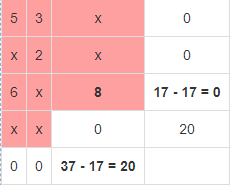



Искомый элемент равен c₄₃=0. Для этого элемента запасы равны 20, потребности 20. Поскольку минимальным является 20, то вычитаем его.

x₄₃ = min(20,20) = 20.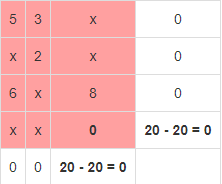



В итоге получаем:

		B1	B2	B3
	ai \ bj	20	12	37
A1	15	5| 13	3| 2	7|
A2	10	3|	2| 10	3|
A3	24	6| 7	4|	8| 17
A4	20	0|	0| 20	0|

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность потребителей удовлетворена, а план соответствует системе ограничений транспортной задачи.

Подсчитаем число занятых клеток таблицы, их 6, а должно быть

m + n - 1 = 6. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 5*13 + 3*2 + 2*10 + 6*7 + 8*17 + 0*20 = 269.

Метод двойного предпочтения

Используя метод двойного предпочтения, построим первый опорный план транспортной задачи. В каждой строке находим минимальный элемент. Ставим напротив него знак V. Затем находим минимальный элемент каждого столбца. Ставим напротив него знак V.

Если таблица стоимостей велика, то перебор всех элементов затруднителен. В этом случае используют метод двойного предпочтения, суть которого заключается в следующем.

В каждом столбце отмечают знаком V клетку с наименьшей стоимостью. Затем то же проделывают в каждой строке. В результате некоторые клетки имеют отметку VV.

В них находится минимальная стоимость, как по столбцу, так и по строке. В эти клетки помещают максимально возможные объемы перевозок, каждый раз исключая из рассмотрения соответствующие столбцы или строки.

Затем распределяют перевозки по ячейкам, отмеченным знаком V. В оставшейся части таблицы перевозки распределяют по наименьшей стоимости.

Искомый элемент находится в клетке (2;2) и равен 2.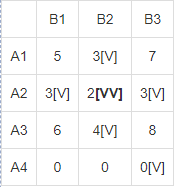



Искомый элемент равен c₂₂=2. Для этого элемента запасы равны 10, потребности 12. Поскольку минимальным является 10, то вычитаем его.

x₂₂ = min(10,12) = 10.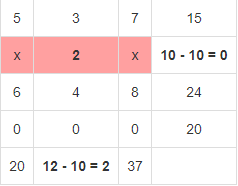



Искомый элемент находится в клетке (1;2) и равен 3.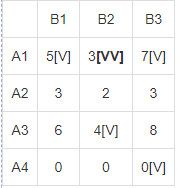



Искомый элемент равен c₁₂=3. Для этого элемента запасы равны 15, потребности 2. Поскольку минимальным является 2, то вычитаем его.

x₁₂ = min(15,2) = 2.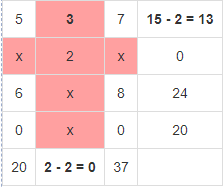



Искомый элемент находится в клетке (1;1) и равен 5.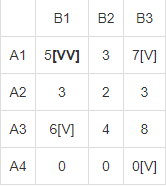



Искомый элемент равен c₁₁=5. Для этого элемента запасы равны 13, потребности 20. Поскольку минимальным является 13, то вычитаем его.

x₁₁ = min(13,20) = 13.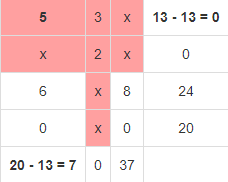



Искомый элемент находится в клетке (3;1) и равен 6.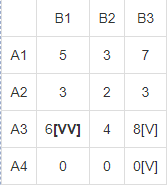



Искомый элемент равен c₃₁=6. Для этого элемента запасы равны 24, потребности 7. Поскольку минимальным является 7, то вычитаем его.

x₃₁ = min(24,7) = 7.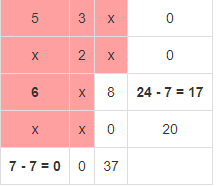



Искомый элемент находится в клетке (3;3) и равен 8.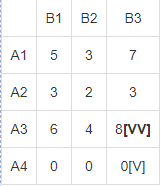



Искомый элемент равен c₃₃=8. Для этого элемента запасы равны 17, потребности 37. Поскольку минимальным является 17, то вычитаем его.

x₃₃ = min(17,37) = 17.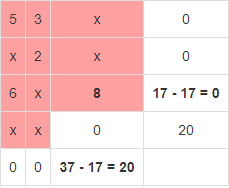



Искомый элемент находится в клетке (4;3) и равен 0.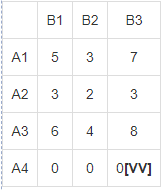



Искомый элемент равен c₄₃=0. Для этого элемента запасы равны 20, потребности 20. Поскольку минимальным является 20, то вычитаем его.

x₄₃ = min(20,20) = 20.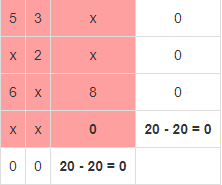



В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

Подсчитаем число занятых клеток таблицы, их 6, а должно быть

m + n - 1 = 6. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 5*13 + 3*2 + 2*10 + 6*7 + 8*17 + 0*20 = 269.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 5; 0 + v₁ = 5; v₁ = 5

u₃ + v₁ = 6; 5 + u₃ = 6; u₃ = 1

u₃ + v₃ = 8; 1 + v₃ = 8; v₃ = 7

u₄ + v₃ = 0; 7 + u₄ = 0; u₄ = -7

u₁ + v₂ = 3; 0 + v₂ = 3; v₂ = 3

u₂ + v₂ = 2; 3 + u₂ = 2; u₂ = -1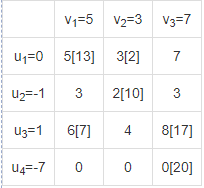



Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(2;1): -1 + 5 > 3; ∆21 = -1 + 5 - 3 = 1 > 0;

(2;3): -1 + 7 > 3; ∆23 = -1 + 7 - 3 = 3 > 0;

max(1,3) = 3.

Выбираем максимальную оценку свободной клетки (2;3): 3.

Для этого в перспективную клетку (2;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

		B1	B2	B3
	ai \ bj	20	12	37
A1	15	5| 13(-)	3| 2(+)	7|
A2	10	3|	2| 10(-)	3| (+)
A3	24	6| 7(+)	4|	8| 17(-)
A4	20	0|	0| 20	0|

Цикл приведен в таблице (2,3 → 2,2 → 1,2 → 1,1 → 3,1 → 3,3).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min(2, 2) = 10. Прибавляем 10 к объемам грузов, стоящих в плюсовых клетках, и вычитаем 10 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 5; 0 + v₁ = 5; v₁ = 5;

u₃ + v₁ = 6; 5 + u₃ = 6; u₃ = 1;

u₃ + v₃ = 8; 1 + v₃ = 8; v₃ = 7;

u₂ + v₃ = 3; 7 + u₂ = 3; u₂ = -4;

u₄ + v₃ = 0; 7 + u₄ = 0; u₄ = -7;

u₁ + v₂ = 3; 0 + v₂ = 3; v₂ = 3.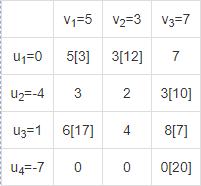



Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_j ≤ c_ij.

Минимальные затраты составят:

F(x) = 5*3 + 3*12 + 3*10 + 6*17 + 8*7 + 0*20 = 239.

Из 1-го склада необходимо груз направить в 1-й магазин (3 ед.), в 2-й магазин (12 ед.)

Из 2-го склада необходимо весь груз направить в 3-й магазин.

Из 3-го склада необходимо груз направить в 1-й магазин (17 ед.), в 3-й магазин (7 ед.)

Потребность 3-го магазина остается неудовлетворенной на 20 ед.

Оптимальный план является вырожденным, так как базисная переменная x₄₃=0.

Проверка

Выполним проверку нахождения оптимального плана в пакете Excel.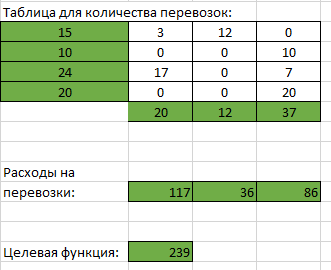



Выполним проверку нахождения оптимального плана в пакете Mathcad.

I способ:



II способ: