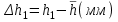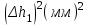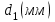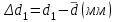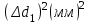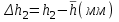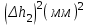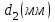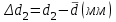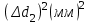Макет лабораторной работы №1, по методичке №3. Лабораторная работа 3 " Измерение линейных величин штангенциркулем и микрометром" Краткая теория работы
 Скачать 237.48 Kb. Скачать 237.48 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №3 “Измерение линейных величин штангенциркулем и микрометром” Краткая теория работы: Без измерений физических величин не обходится ни одна естественная или техническая наука, ни одна отрасль производства. При всяком измерении происходит взаимодействие измеряемого объекта и измерительного прибора. В процессе измерений, как и во всяком действии, происходят ошибки. Ошибки измерений принято подразделять на систематические, случайные и промахи. 1.Что такое систематические ошибки? Рассмотрим несколько примеров. Для того, чтобы измерить силу тока в цепи, используют амперметр, включая его в электрическую цепь. Но уже при этом действии сила тока в цепи обязательно изменится на некоторую (обычно небольшую) величину, потому что амперметр сам обладает сопротивлением. Эту ошибку устранить нельзя, но её можно учесть. Очевидно, что эта ошибка будет всегда одной и той же, если измеряется одно и то же значение тока. 2. Другой пример систематических ошибок измерений - приборные ошибки. Они всегда имеют место из-за несовершенства измерительного прибора. Поскольку трудно определить как будет сказываться несовершенство прибора и его шкалы в каждом конкретном измерении, принято в качестве приборной ошибки использовать максимальную возникшую ошибку прибора (конечно, при добросовестном отношении к делу). 3. Иногда, эту максимальную ошибку называют точностью данного прибора и вводят специальную характеристику прибора – “класс точности”. Например; если “класс точности” прибора 0,1, то это означает, что максимальная приборная ошибка измерений составляет 0,1% от самого большого деления (максимального показания шкалы этого прибора). Если шкала амперметра (класса точности 0,1) имеет деления до 10А, то максимальная приборная ошибка измерений составляет 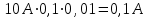 . Эта величина и принимается в качестве приборной ошибки. . Эта величина и принимается в качестве приборной ошибки.Для простых приборов, измеряющих линейные размеры предметов (линейки, штангенциркули, микрометры), классы точности обычно не указываются. В этом случае, часто, за ошибку измерений принимают половину цены самого мелкого деления шкалы. Например: если каждая линейка имеет деления через каждый миллиметр, то приборная ошибка составляет 0,5 мм. Особый случай представляют собой измерения, когда они производятся штангенциркулем с так называемым нониусом. В этом случае ошибка зависит от вида нониуса, от того, сколько он имеет делений. Например: если делений 20, а основная шкала штангенциркуля имеет штрихи через 1 мм., то приборной ошибкой считается 1мм : 20 = 0,05 мм 4. Случайные ошибки измерений - это ошибки, которые в отличие от систематических, имеют разные значения в измерениях, проводимых в одинаковых условиях. Одинаковые условия означают, что имеется один и тот же объект измерений, один и тот же прибор, один и тот же человек производящий измерения. Так, например, если в электрической цепи измеряется сила тока создаваемая батарейкой, то она может изменяться от одного момента времени к другому, из-за того, что в батарейке будут нарушены условия стационарной химической реакции. Если измеряются линейные размеры предметов, например; высота цилиндра, то случайная ошибка измерений связана с тем, что измеряемый объект не является идеальным цилиндром, его основания не представляют собой идеально плоских поверхностей. Поэтому, измерение высоты с одной стороны цилиндра может отличаться от измерения с другой стороны. В этом случае случайная ошибка измерений, характеризует уже не сам процесс измерения, а процесс изготовления этого цилиндра. 5. В данной лабораторной работе проводятся измерения двух линейных размеров цилиндров - высоты и диаметра, а затем, вычисляется объем цилиндра (напомним, что объем прямого цилиндра 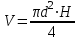 , где , где 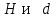 высота и диаметр цилиндра). Результат работы представляется в виде: высота и диаметр цилиндра). Результат работы представляется в виде: 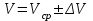 (1) ,где (1) ,где 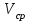 - некоторое среднее измерение объема, a - некоторое среднее измерение объема, a 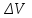 - абсолютная ошибка (погрешность) измерения объема. Величина - абсолютная ошибка (погрешность) измерения объема. Величина 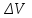 связана как с систематическими ошибками измерений, прежде всего, приборными погрешностями, так и со случайными ошибками измерений, которые определяются несовершенством технологии изготовления объекта измерений. связана как с систематическими ошибками измерений, прежде всего, приборными погрешностями, так и со случайными ошибками измерений, которые определяются несовершенством технологии изготовления объекта измерений. 6. Отличить систематические ошибки от случайных, в этом случае, очень трудно. Поэтому результат измерений следует засчитывать следующим образом: какова точность определения объема цилиндра, если пользоваться для этого простейшей геометрической формулой и производить измерения его диаметра и высоты. (Если объем этого самого цилиндра определять другим способом, например; по измерению его массы, или методом вытеснения жидкости, то область определения объема была бы другая. В этих случаях случайную ошибку измерений, связанную с тем, что этот цилиндр не является идеальным геометрическим цилиндром, удалось бы практически полностью исключить, и ошибка 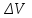 определилась бы, таким образом погрешностями приборов и метода измерения). определилась бы, таким образом погрешностями приборов и метода измерения).7. В данной лабораторной работе измерение объема цилиндра является косвенным измерением. Это означает, что измеряется не сам объем, а те величины, с помощью которых он определяется. 8. Измерения, при которых результат отсчитывается непосредственно по шкале прибора, называются прямыми. Прямыми измерениями, в частности, является измерения высоты и диаметра цилиндра, штангенциркулем и микрометром. В технике измерения часто бывают прямыми (определение температуры, давления и т.д.). Но в лабораторных условиях, часто, необходимо проводить косвенные измерения, то есть, получать какой-либо результат, пользуясь показаниями приборов и производя, затем, необходимые вычисления. Большинство измерений величин определяется косвенным методом. Для того, чтобы определить ошибку косвенных измерений, принято знать ошибки прямых измерений. Поэтому, сначала рассмотрим обработку результатов прямых измерений. Теория этой обработки связана с такими разделами математики как теория вероятности и математическая статистика. Эти разделы, обычно, в ВУЗе изучаются позже чем происходит изучение физики, поэтому, будут использоваться только результаты математических расчетов, без их выводов и доказательства. Допустим, что производится несколько измерений некоторой физической величины X. Все эти- измерения могут несколько отличаться друг от друга. Обозначим результат отдельного измерения X , введем разность:  (2) (2)представляющую собой отклонения каждого отдельного измерения от истинного значения измеряемой величины. Истинное значение прямой* величины X не известно. Поэтому, нужно пользоваться наиболее хорошим приближением к этой величине. В большинстве случаев таким хорошим приближением является среднее арифметическое значение из n измерений:  (3) (3)Из результатов измерений, таким образом, можно брать не отклонения  от истинного значения, а отклонения: от истинного значения, а отклонения:  (4) (4)от среднего значения. В руководстве к работе эти величины названы абсолютными погрешностями отдельных измерений. Но для оценки разности измерений сами абсолютные величины погрешности не достаточны. Теория, которая связывает разность абсолютных погрешностей с прямыми погрешностями достаточно сложна и здесь рассматриваться не будет. Основные ее результаты сводятся к следующему. 9. По результатам измерений можно найти некоторую величину  , которая характеризует точность изменений. Результат измерений, при этом, представляется в виде: , которая характеризует точность изменений. Результат измерений, при этом, представляется в виде:  . Это означает, что значение; измеряемой величины X лежит в пределах от . Это означает, что значение; измеряемой величины X лежит в пределах от  , до , до  . Более точно об измеряемой величине X сказать ничего нельзя. Возможно её значение меньше X, но возможно и больше. Разность величин ( . Более точно об измеряемой величине X сказать ничего нельзя. Возможно её значение меньше X, но возможно и больше. Разность величин ( )-( )-( )=2 )=2 часто называют доверительным интервалом измеряемой величины, а саму величину часто называют доверительным интервалом измеряемой величины, а саму величину  полушириной доверительного интервала. На рисунке представляющей часть числовой оси, полушириной доверительного интервала. На рисунке представляющей часть числовой оси, отрезок AA1 - это доверительный интервал, а отрезок АО и ОА1 - полуширина доверительного интервала. Наиболее существенно при этом то, что даже такая приближенная, оценка величины X не является абсолютно надежной или достоверной (её вероятность не равна I, или 100%), Таким образом, доверительный интервал  - это интервал численный, в который истинная величина попадает с заданной вероятностью. Пусть, например, задана доверительная вероятность 95%. Это означает, что значение измеряемой величины находится в пределах от - это интервал численный, в который истинная величина попадает с заданной вероятностью. Пусть, например, задана доверительная вероятность 95%. Это означает, что значение измеряемой величины находится в пределах от  до до  с вероятностью 95%. При этом существует 5%-ная вероятность того, что истинное значение измеренной величины находится вне пределов доверительного интервала - либо меньше, чем с вероятностью 95%. При этом существует 5%-ная вероятность того, что истинное значение измеренной величины находится вне пределов доверительного интервала - либо меньше, чем  , либо больше, чем , либо больше, чем  . Если такое значение X является недопустимым по технологическим нормам, о может привести к браку (аварии), то вероятность появления брака (его процент) может быть рассчитана, зная доверительную, вероятность данного конкретного измерения. В данной лабораторной работе принято, что доверительная вероятность 95% является вполне достаточной для выполнения цели работы - определение возможности измерять объем цилиндра через измерение его диаметра и высоты. . Если такое значение X является недопустимым по технологическим нормам, о может привести к браку (аварии), то вероятность появления брака (его процент) может быть рассчитана, зная доверительную, вероятность данного конкретного измерения. В данной лабораторной работе принято, что доверительная вероятность 95% является вполне достаточной для выполнения цели работы - определение возможности измерять объем цилиндра через измерение его диаметра и высоты.10. Таким образом, утверждать, что значение измеряемой величины находится в пределах доверительного интервала, можно лишь с определенной, "доверительной" вероятностью X, и, следовательно, полуширина доверительного интервала является функцией доверительной вероятности:  (5). Поэтому, если результат измерений представлен с заданной степенью надежности (доверительной вероятности) (5). Поэтому, если результат измерений представлен с заданной степенью надежности (доверительной вероятности)   то теория позволяет представить его с любой другой доверительной вероятностью то теория позволяет представить его с любой другой доверительной вероятностью   . При нахождении . При нахождении  методика следующая. Полуширина доверительного, интервала методика следующая. Полуширина доверительного, интервала  представляется, как произведение двух величин: представляется, как произведение двух величин:  (6), где (6), где  так называемая средне-квадратичная погрешность среднего арифметического, так называемая средне-квадратичная погрешность среднего арифметического,  - коэффициент Стьюдента, а - коэффициент Стьюдента, а  - число измерений. Запись - число измерений. Запись  означает, что величина коэффициента Стьюдента t, а также и означает, что величина коэффициента Стьюдента t, а также и  зависит как от доверительной вероятности так и от числа измерений зависит как от доверительной вероятности так и от числа измерений  . Стьюдент ("Студент") - научный псевдоним английского, математика. . Стьюдент ("Студент") - научный псевдоним английского, математика.11. Для выбранного значения вероятности (  0,95) составляет – 2. (в некоторых условных единицах). Если сделано 2 измерения, то нельзя утверждать что с вероятностью 95% значение измеряемой величины находится в этом доверительном интервале. Можно ручаться только за больший интервал, равный 2,12. Если число измерений 10, то при той же доверительной вероятности доверительный интервал еще больше - 2,34 , при 5 измерениях – 8. Приведенные цифры - 2;3,4;2,8 являются значениями коэффициента Стьюдента соответственно для 5, 10 и 20 измерений, при доверительной вероятности 0,95% 0,95) составляет – 2. (в некоторых условных единицах). Если сделано 2 измерения, то нельзя утверждать что с вероятностью 95% значение измеряемой величины находится в этом доверительном интервале. Можно ручаться только за больший интервал, равный 2,12. Если число измерений 10, то при той же доверительной вероятности доверительный интервал еще больше - 2,34 , при 5 измерениях – 8. Приведенные цифры - 2;3,4;2,8 являются значениями коэффициента Стьюдента соответственно для 5, 10 и 20 измерений, при доверительной вероятности 0,95%12. При других значениях доверительной вероятности значения коэффициента Стьюдента другие. Чем больше доверительная вероятность, тем больше значение коэффициента. Стьюдента (больше доверительный интервал). Чем больше число измерений (при данной доверительной вероятности), тем меньше коэффициент Стьюдента.  13. Величина  в формуле (6) - среднеарифметическая погрешность среднего в формуле (6) - среднеарифметическая погрешность среднегоарифметического (в руководстве к работе она называется "средневероятная погрешность результата серии прямых измерений") определяется по формуле:   - число измерений, а - число измерений, а  - абсолютная погрешность отдельного измерения. Изложенные выше результаты теории используются для подсчета случайных ошибок измерений, что в данной работа, связано с изготовлением объектов измерения. Для того, чтобы учесть и систематические (приборные) погрешности, величину полуширины доверительного интервала следует увеличить согласно формуле: - абсолютная погрешность отдельного измерения. Изложенные выше результаты теории используются для подсчета случайных ошибок измерений, что в данной работа, связано с изготовлением объектов измерения. Для того, чтобы учесть и систематические (приборные) погрешности, величину полуширины доверительного интервала следует увеличить согласно формуле:  (7) (7)где - полушария доверительного интервала без учета приборной ошибки,  - абсолютная погрешность прибора. Если - абсолютная погрешность прибора. Если  окажется существенно больше окажется существенно больше  (в 3 или более число раз), от (в 3 или более число раз), от  (с разностью до 5%). (с разностью до 5%).14. Относительная ошибка прямого измерения - это отношение суммарной полуширины доверительного интервала  к средней арифметической величине: к средней арифметической величине:   (8) (8)Измерение объема цилиндра в данной работе является косвенным измерением. Теория ошибок косвенных измерений достаточно сложна здесь будут приведены только основные её результаты. Измеряемая величина А - есть функция от других величин (Х1, X2, X3). В нашем случае объем цилиндра V есть функция его диаметра d и высоты h. В результате прямых измерений находятся среднеарифметические величины Х1, X2, X3 (в нашем случае  и и  ), полуширина их доверительных интервалов ), полуширина их доверительных интервалов  и относительные погрешности и относительные погрешности  . В том случае, если косвенным образом величина А зависит от: Х1, X2, X3 как степенная функция: . В том случае, если косвенным образом величина А зависит от: Х1, X2, X3 как степенная функция:  (8)то относительная ошибка косвенного измерения находится по формуле: (8)то относительная ошибка косвенного измерения находится по формуле:  (9) Например, если косвенно измеряется мощность, выделенная в цепи электрического тока через измерение напряжения сопротивления (9) Например, если косвенно измеряется мощность, выделенная в цепи электрического тока через измерение напряжения сопротивления  и определены относительные погрешности и определены относительные погрешности  и и  то, относительная, погрешность измерения мощности: то, относительная, погрешность измерения мощности:  В нашем случае: В нашем случае:  Для того, чтобы найти абсолютную погрешность косвенного измерения, находят среднее значение косвенного измерения через средние арифметические значения прямых измерений. B нашем случае: Для того, чтобы найти абсолютную погрешность косвенного измерения, находят среднее значение косвенного измерения через средние арифметические значения прямых измерений. B нашем случае:  При этом возникает необходимость решать вопрос, сколько значащих цифр нужно брать в частности для значения числа. Соответствующий прием изложен в руководстве к работе. Относительный результат измерений представлен в виде: При этом возникает необходимость решать вопрос, сколько значащих цифр нужно брать в частности для значения числа. Соответствующий прием изложен в руководстве к работе. Относительный результат измерений представлен в виде:  где где  поскольку поскольку  . .15. Как следует из вышеизложенного, этот результат свидетельствует о том, что истинное значение объема прямого цилиндра находится в пределе от  до до  с доверительной вероятностью 0,95%. Неточность этого косвенного приема связана как с погрешностями приборов (штангенциркуля и микрометра), так и со случайными погрешностями, имевшими место при изготовлении цилиндра, которые привели к случайным ошибкам измерении диаметра и высоты цилиндра. с доверительной вероятностью 0,95%. Неточность этого косвенного приема связана как с погрешностями приборов (штангенциркуля и микрометра), так и со случайными погрешностями, имевшими место при изготовлении цилиндра, которые привели к случайным ошибкам измерении диаметра и высоты цилиндра.16. Измерение объема, проведенное прямым способом (например по вытеснению жидкости), дали бы меньшее значение случайной ошибки, поскольку при этом погрешности при изготовлении цилиндра не играли бы роли. При той же доверительной вероятности значение доверительного интервала было бы меньшим. Вопросы, связанные с осуществлением приближенных вычислений, с построением графиков и другие вопросы в настоящей краткой теории не обсуждаются, а могут быть изучены самостоятельно по предлагаемой литературе. ИЗМЕРЕНИЕ ШТАНГЕНЦИРКУЛЕМ Для измерения размеров деталей с точностью до десятых долей миллиметра применяют штангенциркуль. Основная часть его - линейка с сантиметровыми и миллиметровыми делениями /цена деления I мм/. На одном из концов линейки закреплена ножка. По линейке скользит рамка с другой ножкой. В рамке сделано окошко, по внутреннему краю которого нанесена шкала - нониус. Десять делений этой шкалы равны 9 мм, а одно деление, следовательно, составляет 0,9 мм. У некоторых штангенциркулей на рамке имеются 20 делений, соответствующих 19 мм шкалы линейки. При соприкосновении ножек штангенциркуля нули обеих шкал совпадают. Для определения размеров детали ее зажимают между ножками штангенциркуля и по положению нулевого штриха нониуса на шкале линейки определяют число целых миллиметров. Затем смотрят, какой из штрихов шкалы нониуса, считая от нулевого совпадает со штрихом шкалы на линейке. Полученное число соответствует числу десятых долей миллиметра. Размер детали получают сложением числа целых миллиметров, отсчитанных по линейке и десятых долей миллиметра, отсчитанных по шкале нониуса. Рассмотрим принцип действия нониуса. Если сомкнуть вплотную ножки циркуля, то нулевой штрих нониуса точно совпадает с нулевым штрихом линейки. Первый штрих нониуса не дойдет до первого штриха линейки на 0,1 мм, так как одно деление нониуса на ОД мм меньше одного деления шкалы линейки; второй штрих нониуса не дойдет до второго штриха линейки на 0,2 мм: третий - на 0,3 мм и т.д. Если сдвинуть движок так, чтобы первый штрих нониуса /не считая нулевого / совпал с первым штрихом линейки, то между ножками штангенциркуля получится зазор 0,1 мм. При совпадении второго штриха нониуса со вторым штрихом линейки зазор между ножками будет 0,2 мм и т.д. Следовательно, тот штрих нониуса, который точно совпадает с каким-либо штрихом линейки, покажет число десятых долей миллиметра между ножками штангенциркуля. Нередко нониус применяют с микроскопом. В этом случае деления нониуса сделаны очень мелкими, что позволяет производить более точные измерения. ПОРЯДОК ВЫПОНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ № 3 ИЗМЕРЕНИЕ ЛИНЕЙНЫХ ВЕЛИЧИН ШТАНГЕНЦИРКУЛЕМ И МИКРОМЕТРОМ. В тетради сделать таблицу следующего вида: Тело 1
h=25,34 d=24.74 Тело 2
h=16,5 d=15.64 Измерить высоту цилиндра hi штангенциркулем, и диаметр цилиндра di микрометром. Данные измерения проделать 5 раз в различных точках цилиндра. Результаты измерений занести в таблицу. Рассчитайте среднее арифметическое значение высоты 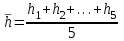 и диаметра и диаметра 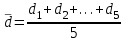 цилиндра. Результаты вычислений записать в таблицу, округлив до 0,01. цилиндра. Результаты вычислений записать в таблицу, округлив до 0,01.Вычислить абсолютные погрешности измерений высоты и диаметра цилиндра: 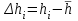 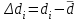 . Результаты занести в таблицу. . Результаты занести в таблицу.Вычислите величины 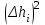 и и 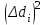 . Результаты занести в таблицу. . Результаты занести в таблицу.Определите среднеквадратичные погрешности произведенных вами измерений по формулам: 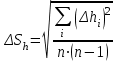 ; ; 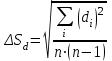 . n –число измерений( в данной работе оно равно 5).При вычислении результат округлите до сотых.. . n –число измерений( в данной работе оно равно 5).При вычислении результат округлите до сотых..Определить погрешность результата измерении (полуширину доверительного интервала): 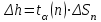 ; ; 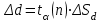 ; ; 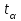 - коэффициент Стьюдента ( для данной работы его принять равным 2,8); - коэффициент Стьюдента ( для данной работы его принять равным 2,8); 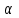 -доверительная вероятность ( -доверительная вероятность (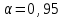 ). Величина погрешности результата измерений окажется сравнимой с величиной погрешности прибора или меньше ее ( для штангенциркуля ). Величина погрешности результата измерений окажется сравнимой с величиной погрешности прибора или меньше ее ( для штангенциркуля 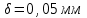 , для микрометра , для микрометра 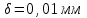 ). В качестве полуширины доверительного интервала следует взять величину ). В качестве полуширины доверительного интервала следует взять величину 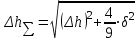 ; ; 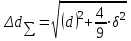 . .Вычислить относительные погрешности измерения высоты 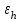 и диаметра и диаметра 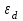 цилиндра с точностью до двух значащих цифр: цилиндра с точностью до двух значащих цифр: 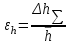 ; ; 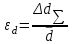 . .Определите относительную ошибку измерения объема цилиндра по формуле: 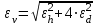 . .Определить необходимое число значащих цифр в числе 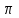 . Для этого вычислить . Для этого вычислить 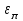 по формуле по формуле 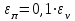 и использовать следующую таблицу: и использовать следующую таблицу: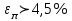 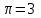 ; ; 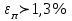 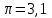 ; ; 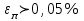 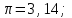 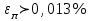 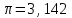 . .Найдите среднее значение объема  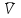 по формуле: по формуле: 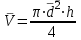 . .Определить абсолютную погрешность измерения объема по формуле: 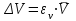 . .Окончательный результат записать в виде 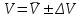 с учетом соответствующего количества значащих цифр. Например: V=(4,39 с учетом соответствующего количества значащих цифр. Например: V=(4,39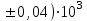 . .14.Измерения и расчеты повторить для второго тела. Контрольные вопросы 1. Какие бывают ошибки измерений? 2. Что принимается в качестве приборной ошибки измерений? 3. Что такое “класс точности” прибора? 4. В чем отличие случайных ошибок от систематических? 5.Каковы систематические (приборные)ошибки в данной работе? 6.Какова причина случайных ошибок в данной работе? 7. Что такое косвенные измерения? 8. Что такое “абсолютная погрешность .прямого измерения”? 9. Что такое “относительная ошибка прямого измерения”? 10. Что такое “доверительный интервал” и “доверительная вероятность”? 11. Как вычисляется “доверительный интервал”? 12. Как изменяется величина доверительного интервала с увеличением доверительной вероятности? 13. Как зависит величина доверительного интервала от числа измерений? 14. В какой величине стремиться величина доверительного интервала для доверительной вероятности? 15. Как угадываются систематические (приборные) погрешности при определении абсолютной ошибки измерений? 16. Как вычисляется среднее значение косвенного измерения? 17. Как вычисляется относительная и абсолютная погрешность косвенного измерения (на конкретных примерах)? 18. Что означает, что определенный вами объем цилиндра имеет погрешность? 19. Что Вы можете сказать об ошибке измерений объема цилиндра другими методами? |