Лабораторная работа 3, Коневец Арсений Б9120-09.03.03пикд. Лабораторная работа 3 1) 2) 3) Решить систему ( ) Изобразим схему множеств
 Скачать 34.51 Kb. Скачать 34.51 Kb.
|
|
Коневец Арсений Лабораторная работа №3 1) 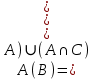 : :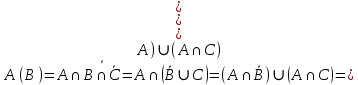 ; ;2) 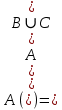 : : ; ;3) Решить систему ( 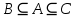 ) ) : :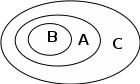 Изобразим схему множеств: Согласно схеме, из первого уравнения в системе вытекает, что 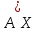 , а из второго - , а из второго - 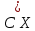 , объединим эти два множества и получим ответ: , объединим эти два множества и получим ответ: 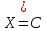 . .4) 5) Найти все подмножества множеств 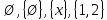 : :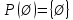 ; ; ; ; ; ; . .6) A и B – конечные множества из m и n элементов соответственно: а) Сколько существует бинарных отношений между А и В: Между А и В существует 2n*m бинарных отношений. б) Сколько существует функций из A в B: Между А и В существует nm функций. в) Сколько существует 1-1-функций из A в B: Между А и В существует  инъективных функций. инъективных функций.г) При каких условиях существует взаимно-однозначное соответствие между A и B: Взаимно-однозначное соответствие между А и В может существовать только в том случае, если их мощности равны: n = m. 7) Доказать, что для того, чтобы отношение  было взаимно-однозначным соответствием между A и B, необходимо и достаточно, чтобы RR-1=iA и R-1R=iB: было взаимно-однозначным соответствием между A и B, необходимо и достаточно, чтобы RR-1=iA и R-1R=iB:Предположим, что R – взаимно-однозначное соответствие, тогда 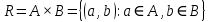 , ,  . .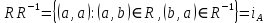 ; ;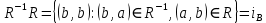 . .8) Доказать, что отношение R на A является эквивалентностью и частичным порядком одновременно тогда и только тогда, когда R = iA: Чтобы отношение являлось эквивалентностью, необходимо чтобы оно было рефлексивным, симметричным и транзитивным; чтобы являлось частичным порядком, оно должно быть рефлексивным, антисимметричным и транзитивным. Рефлексивность и транзитивность требуются и для эквивалентности, и для частичного порядка, их доказательство не требуется. Возникает конфликт: отношение должно быть одновременно симметричным и антисимметричным: 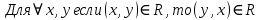 - симметричность; - симметричность; 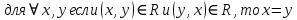 – антисимметричность. – антисимметричность.Оба этих требования будут соблюдаться тогда и только тогда, когда 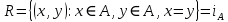 . .9) Доказать, что множество всех подмножеств заданного множества частично упорядочено отношением ⊆: Докажем, что отношение включения является отношением частичного порядка, для этого оно должно обладать свойствами рефлексивности, антисимметричности и транзитивности:  ; ; ; ; . .Следовательно, отношение включения является отношением частичного порядка, а, значит, может частично упорядочить множество всех подмножеств данного множества. 10) а) Доказать, что любое частично упорядоченное множество содержит не более одного наименьшего/наибольшего элемента: По определению, a – наименьший/наибольший элемент множества A, если  . .Докажем от противного: предположим, что в множестве два наименьших элемента: a1 и a2, тогда по определению:  , по свойству антисимметричности имеем: , по свойству антисимметричности имеем:  => наименьший элемент только один. => наименьший элемент только один.б) Доказать, что наименьший/наибольший элемент единственен: Доказано в предыдущем задании. в) Привести пример частично упорядоченного множества, у которого есть один минимальный элемент, но нет максимального: Примером такого частично упорядоченного множества может являться полуинтервал  , у него будет один минимальный элемент (n), однако m не будет являться максимальным, так как оно не входит в промежуток – максимальный элемент отсутствует. , у него будет один минимальный элемент (n), однако m не будет являться максимальным, так как оно не входит в промежуток – максимальный элемент отсутствует.11) Построить линейный порядок на множестве 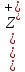 : :Мы можем определить любое отношение частичного порядка на 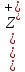 , например, можем сказать, что , например, можем сказать, что  , если , если 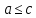 (если (если 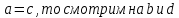 ). Таким образом, этим отношением можно построить линейный порядок на множестве. ). Таким образом, этим отношением можно построить линейный порядок на множестве.12) Доказать, что если некоторое отношение < на A иррефлексивно и транзитивно, то отношение ≤: x ≤ y <=> x < y \/ x = y является частичным порядком: Чтобы отношение являлось частичным порядком, необходимо, чтобы оно обладало свойствами рефлексивности, антисимметричности и транзитивности: Дано, что x ≤ y <=> x < y \/ x = y => a ≤ a => ≤ рефлексивно; Также из условия: если x ≤ y и y ≤ x, то всегда будет истинным второе условие: x = y => ≤ антисимметрично; Транзитивность по условию. Следовательно, такое отношение будет являться частичным порядком. 13) Доказать, что любое непустое конечное частично упорядоченное множество содержит минимальный и максимальный элементы: Докажем по индукции: Если |A| = 1, то его единственный элемент будет являться максимальным и минимальным; Рассмотрим множество A, |A| = k. Предположим, что в нем имеется максимальный элемент m, то есть  . Увеличим размер множества на 1 (|A| = k + 1), добавив элемент x, тогда x может стать максимальным, если . Увеличим размер множества на 1 (|A| = k + 1), добавив элемент x, тогда x может стать максимальным, если  (по транзитивности: если (по транзитивности: если  и и  , то , то  => x - максимальный) => в множестве все еще будет существовать максимальный элемент; если же x не станет максимальным, то в нем максимальным останется m => в множестве существует максимальный элемент. Аналогично для минимального элемента. => x - максимальный) => в множестве все еще будет существовать максимальный элемент; если же x не станет максимальным, то в нем максимальным останется m => в множестве существует максимальный элемент. Аналогично для минимального элемента.14) k - натуральное число. Доказать, что существует натуральное n такое, что k | n и записано с использованием только нулей и троек: Для доказательства воспользуемся принципом голубиных клеток. Зададим множество чисел {3, 33, 333, 3333…} из k + 1 элементов. В этом множестве разность двух любых чисел будет натуральным числом, состоящим из 0 и 3. Согласно принципу голубиных клеток, в этом множестве будет как минимум два числа, остаток от деления которых на k будет одинаковым (так как чисел k + 1, k делителей, значит как минимум одно число будет иметь такой же остаток, как у одного из остальных). Это означает, что их разность будет делиться на k и состоять лишь из 0 и 3. |
