Главная страница
Навигация по странице:

  • ЛАБОРАТОРНАЯ РАБОТА №3 ПО ДИСЦИПЛИНЕ «ОБРАБОТКА СИГНАЛОВ» ДИСКРЕТИЗАЦИЯ И СПЕКТРЫ СИГНАЛОВГруппа

  • Преподаватель

  • Результаты выполнения заданий

  • Выводы по работе

    		•

    ДИСКРЕТИЗАЦИЯ И СПЕКТРЫ СИГНАЛОВ. ОС Л3. Лабораторная работа 3 по дисциплине обработка сигналов дискретизация и спектры сигналов группа авт318


    Скачать 400.02 Kb.
    НазваниеЛабораторная работа 3 по дисциплине обработка сигналов дискретизация и спектры сигналов группа авт318
    АнкорДИСКРЕТИЗАЦИЯ И СПЕКТРЫ СИГНАЛОВ
    Дата22.02.2022
    Размер400.02 Kb.
    Формат файлаdocx
    Имя файлаОС Л3.docx
    ТипЛабораторная работа
    #370339


    Министерство образования и науки РФ

    Федеральное Государственное Бюджетное Образовательное

    Учреждение высшего Образования

    «Новосибирский Государственный Технический Университет»

    фАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

    Кафедра вычислительной техники

    ЛАБОРАТОРНАЯ РАБОТА №3

    ПО ДИСЦИПЛИНЕ «ОБРАБОТКА СИГНАЛОВ»

    ДИСКРЕТИЗАЦИЯ И СПЕКТРЫ СИГНАЛОВ

    Группа: АВТ-318

    Студент: Калытюк И.С. Преподаватель: Рабинович Е.В.

    Новосибирск 2016

    Содержание


    Цель работы 2

    Задание 2

    Результаты выполнения заданий 3

    Выводы по работе 4

    Приложение А 4

    Цель работы

    Целью данной лабораторной работы является ознакомление со свойствами непрерывных, дискретных и цифровых сигналов. Изучение на базе пакета MatLAB спектров периодических и непериодических цифровых сигналов с помощью дискретного преобразования Фурье.

    Задание

    1. Выбрать сигнал s(t) из таблицы согласно варианту I. (I=8)

    s(t)=sinΩt/Ωt, где Ω= 1.

    2. Написать m-функцию lab3, которая, используя быстрое преобразование Фурье, строит модуль и аргумент комплексной спектральной плотности непериодического сигнала s(k).

    3. Выбрать сигнал s(t) из таблицы согласно варианту с номером IТ = 16 + I и построить модуль и аргумент комплексного спектра периодического сигнала sT(k), полученного из сигнала s(k).

    M-функция lab3 должна обладать сигнатурой:

    function [signal,time,amp_spectrum,phase_spectrum,frequency,params] = lab3(SigH,AmpH,PhH)

    end

    Входными параметрами m-функции lab3 являются дескрипторы осей координат, в которых осуществляется вывод сигнала, его амплитудного и фазового этой спектров:

    SigH - дескриптор оси координат для вывода исходного сигнала;

    AmpH - дескриптор оси координат для вывода амплитудного спектра;

    PhH - дескриптор оси координат для вывода фазового спектра.

    Выходными параметрами m-функции lab3 являются:

    signal - сигнал;

    time - время;

    amp_spectrum - амплитудный спектр сигнала;

    phase_spectrum - фазовый спектр сигнала;

    frequency - частота;

    params - дополнительные параметры для пункта 2 располагаются в столбце «Параметры» Таблицы после знака «;». Параметры передаются в том порядке, в котором они указаны (Например, для пятого варианта: params = [L tau]). Для пункта 3 параметры перечисляются, начиная с дополнительного параметра - периода повторения Т.

    4. Проверить правильность построения. Для этого скопировать содержимое папки SP_lab3_Matlab, расположенную в папке «Обработка сигналов», в рабочую папку, содержащую m-функцию lab3. Запустить программу spectrum.p, выбрать в ней вариант и нажать кнопку Проверить.

    Результаты выполнения заданий



    Рис. 1 - Представление единичного сигнала, амплитудного спектра и фазового спектра.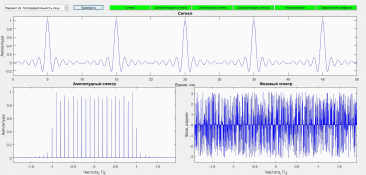



    Рис. 2 - Представление периодического сигнала, амплитудного спектра и фазового спектра.

    На рисунке 1 представлены графики единичного импульса синуса Котельникова, амплитудного и фазового спектров.

    На рисунке 2 представлены графики периодического сигнала с периодом T=10, согласно варианту, амплитудного и фазового спектров.

    Выводы по работе

    Для построения периодических сигналов стоит использовать функцию repmat (pulse, 1, 100).

    Приложение А


    Листинг m-файла lab3.m:

    %% Основная функция, которая вызывается программой spectrum

    function [signal, time, amplitude_spectrum, phase_spectrum, frequency, params] = lab3(SigH, AmpH, PhaseH)

    var = input('Введите вариант: ');

    switch(var)

    case 8

    %% Вариант 8. Синус Котельникова

    omega = 1;

    params = omega;

    Tm = 100;

    Fs = 1024;

    time = -Tm/2:1/Fs:Tm/2;

    signal = sinc(2*omega*time);

    case 24

    %% Вариант 24. Поледовательность синусов Котельникова

    T = 10;

    omega = 1;

    params = [T omega];

    s = 64;

    Tm = 100*T;

    pulse_time = -T/2:1/Fs:(T/2-1/Fs);

    pulse = sinc(2*omega*pulse_time);

    time = 0:1/Fs:(Tm-1/Fs);

    signal = repmat(pulse, 1, 100);

    end

    %% Преобразование Фурье

    NFFT = Fs*Tm;

    FFT_res = fft(signal, NFFT);

    FFT_res = 2*FFT_res./NFFT;

    FFT_res = fftshift(FFT_res);

    frequency=-Fs/2:Fs/NFFT:Fs/2-Fs/NFFT;

    col = 'b';

    %% График исходного сигнала

    axes(SigH);

    plot(time, signal, col);

    if ismember(var, [17:32 0])

    xlim([0 T*5]);

    else

    if ismember(var, [2 4 6 8 11 13 16])

    l_signal = time(find(signal > 0.01, 1, 'first'));

    r_signal = time(find(signal > 0.01, 1, 'last'));

    s_range = r_signal - l_signal;

    xlim([r_signal-s_range*1.1 l_signal+s_range*1.1]);

    else

    l_signal = time(find(signal = 0, 1, 'first'));

    r_signal = time(find(signal = 0, 1, 'last'));

    s_range = r_signal - l_signal;

    xlim([r_signal-s_range*1.1 l_signal+s_range*1.1]);

    end

    end

    ylim(y_lims(signal));

    xlabel('Время, сек');

    ylabel('Амплитуда');

    title('Сигнал');

    %% График амплитудного спектра

    axes(AmpH);

    amplitude_spectrum = abs(FFT_res);

    amplitude_spectrum = amplitude_spectrum./max(amplitude_spectrum);

    if(ismember(var, 0:32) && isnan(max(amplitude_spectrum)))

    end

    if(max(amplitude_spectrum) = 0)

    plot(frequency, amplitude_spectrum./max(amplitude_spectrum), col);

    else

    plot(frequency, amplitude_spectrum, col);

    end

    if ismember(var, [0 17])

    xlim([-maxFrequency*1.1 maxFrequency*1.1]);

    else

    l_signal = frequency(find(amplitude_spectrum > 0.01, 1, 'first'));

    r_signal = frequency(find(amplitude_spectrum > 0.01, 1, 'last'));

    s_range = r_signal - l_signal;

    xrange = [r_signal-s_range*1.1 l_signal+s_range*1.1];

    xlim(xrange);

    end

    ylim(y_lims(amplitude_spectrum./max(amplitude_spectrum)));

    xlabel('Частота, Гц');

    ylabel('Амплитуда');

    title('Амплитудный спектр');

    %% График фазового спектра

    axes(PhaseH);

    phase_spectrum = angle(FFT_res);

    plot(frequency, phase_spectrum, col);

    if ismember(var, [0 17])

    xlim([-maxFrequency*1.1 maxFrequency*1.1]);

    else

    xlim(xrange);

    end

    ylim(y_lims(phase_spectrum));

    xlabel('Частота, Гц');

    ylabel('Фаза, радиан');

    title('Фазовыйспектр');

    set(SigH, 'NextPlot', 'replace');

    set(AmpH, 'NextPlot', 'replace');

    set(PhaseH, 'NextPlot', 'replace');

    end

    %% Корректное отображение графиков по оси ординат

    function ylims = y_lims(signal)

    s_max = max(signal);

    s_min = min(signal);

    range = s_max-s_min;

    middle = (s_max+s_min)/2;

    if(range == 0)

    y_min = s_max-s_max;

    y_max = s_max+s_max;

    else

    y_min = middle-1.15*range/2;

    y_max = middle+1.15*range/2;

    end

    ylims = [y_min y_max];

    end

    написать администратору сайта