Вопросы к защите Лаб. 261 (практическая часть)
 Скачать 45.16 Kb. Скачать 45.16 Kb.
|
|
ВОПРОСЫ к защите Лаб. 26-1 (практическая часть) ____________________________________________________________________ Запишите выражения для прямого и обратного Z-преобразованиий. _______________________________________________________________________ Чему равно Z-преобразование единичного импульса и Z-преобразование задержанного на 3 отсчета единичного импульса? _______________________________________________________________________ Как называется отклик ЦФ на воздействие в виде единичного импульса, привести график этого импульса и его математическое описание? _____________________________________________________________________ Поясните свойства Z-преобразования и запишите их математически (всего четыре свойства). Записать выражение Y(z) для Z-преобразования сигнала {yi} на выходе нерекурсивного ЦФ 3-го порядка, если Z-преобразование X(z) входного сигнала {xi} известно. Записать выражение Y(z) для Z-преобразования сигнала {yi} на выходе нерекурсивного ЦФ 5-го порядка, если Z-преобразование X(z) входного сигнала {xi} известно. ______________________________________________________________________ Как определяется порядок ЦФ и записать общий вид разностного уравнения для ЦФ 3-го порядка ? _______________________________________________________________________ При каком воздействии отклик ЦФ называется переходной функцией, привести график этого воздействия и его математическое описание? _______________________________________________________________________ Коэффициенты разностного уравнения нерекурсивного ЦФ-1 равны b0=1, b1=0.5. Вычислить значение импульсной реакции при n=0 и n=1. _______________________________________________________________________ Параметры нерекурсивного ЦФ-2 равны b0=1, b1=0.5, b2=0.8. Запишите численное значение переходной функции при n = 1. _______________________________________________________________________ Требуется ли проверять на устойчивость нерекурсивный ЦФ и почему (ответ пояснить через рекуррентное уравнение такого фильтра)? _______________________________________________________________________ На нерекурсивный ЦФ 2 порядка с коэффициентами b0=b1=b2=1 действует сигнал  , состоящий из трех ненулевых временных отсчетов: , состоящий из трех ненулевых временных отсчетов:  , , . Записать уравнение такого фильтра и найти каково значение его отсчета отклика . Записать уравнение такого фильтра и найти каково значение его отсчета отклика  ? ?_______________________________________________________________________ Как называется ЦФ, если все его коэффициенты ai=0, и записать его разностное уравнение применительно к ЦФ n-го порядка? _______________________________________________________________________ Как определяется системная функция ЦФ и записать ее выражение применительно к нерекурсивному ЦФ n-го порядка? _________________________________________________________________ Записать разностное уравнение и системную функцию для нерекурсивного ЦФ 4-го порядка с коэффициентами b0=b1=0, b2≠0, b3≠0, b4≠0 ______________________________________________________________________ На нерекурсивный ЦФ 2 порядка с коэффициентами b0=b1=b2=1 действует сигнал 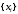 , состоящий из четырех ненулевых временных отсчетов. , состоящий из четырех ненулевых временных отсчетов. 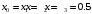 , ,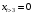 . Записать уравнение такого фильтра и найти каково максимальное значение отсчета отклика фильтра . Записать уравнение такого фильтра и найти каково максимальное значение отсчета отклика фильтра 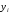 ? ?________________________________________________________________ Осуществляет ли нерекурсивный ЦФ 1 порядка полосовую фильтрацию (ответ обосновать через общее выражение для АЧХ этого фильтра)? ________________________________________________________________ На нерекурсивный ЦФ 2 порядка с коэффициентами b0=b1=b2=1 действует сигнал 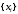 , состоящий из пяти временных отсчетов: , состоящий из пяти временных отсчетов: 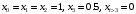 . Сколько не нулевых отсчетов содержит отклик фильтра . Сколько не нулевых отсчетов содержит отклик фильтра 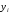 ? ?__________________________________________________________________ Как называется модуль комплексного коэффициента передачи 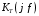 ЦФ и запишите его выражение применительно к нерекурсивному фильтру 3-го порядка? ЦФ и запишите его выражение применительно к нерекурсивному фильтру 3-го порядка?______________________________________________________________________ Как называется отклик ЦФ на воздействие в виде единичной функции включения (скачка) 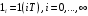 привести график этого воздействия и его математическое описание? привести график этого воздействия и его математическое описание?____________________________________________________________________ Запишите разностное уравнение для нерекурсивного ЦФ n-го порядка и выражение для его комплексного коэффициента передачи. ____________________________________________________________________ Что такое дискретная свертка двух сигналов и чему равно ее Z-преобразование (ответ пояснить соответствующими формулами)? _____________________________________________________________________ Нарисовать структурную схему нерекурсивного ЦФ 4-го порядка и c записать его разностное уравнение (все коэффициенты b0,..,b4 не нулевые). Вывести выражение для АЧХ нерекурсивного ЦФ 1-го порядка с произвольными коэффициентами b0, b1 (ответ преобразовать к максимально простому виду). ___________________________________________________________________ При каких ограничениях на коэффициенты b0, b1получается ЦФ-1 верхних частот (ответ обосновать анализом соответствующего выражения для АЧХ ЦФ-1) _________________________________________________________________ При каких ограничениях на коэффициенты b0, b1 получается ЦФ-1 нижних частот (ответ обосновать анализом соответствующего выражения для АЧХ ЦФ-1) ________________________________________________________________ Вывести выражение для ИХ нерекурсивного ЦФ 1-го порядка с произвольными коэффициентами b0, b1 (непосредственно воспользоваться определением ИХ, разностным уравнением и ответ преобразовать к максимально простому виду). __________________________________________________________________ Вывести выражение для ИХ нерекурсивного ЦФ 2-го порядка с произвольными коэффициентами b0, b1, b2 (непосредственно воспользоваться определением ИХ, разностным уравнением и ответ преобразовать к максимально простому виду). _______________________________________________________________ Нарисовать структурную схему нерекурсивного ЦФ 3-го порядка и c записать его разностное уравнение, если коэффициенты b0 =b2=0, b1≠0, b3≠0. ____________________________________________________________________ Нарисовать структурную схему нерекурсивного ЦФ 3-го порядка и c записать его разностное уравнение, если коэффициенты b0≠0, b1=0, b2≠0, b3≠0. ____________________________________________________________________ Нарисовать структурную схему нерекурсивного ЦФ 3-го порядка и c записать его разностное уравнение, если коэффициенты b0= b1 =b2=0, b3≠0 ____________________________________________________________________ |
