Лабораторная работа 3 Расчёт распределения токов в электрической цепи. Постановка задачи Задана электрическая цепь
 Скачать 370.73 Kb. Скачать 370.73 Kb.
|
|
Лабораторная работа №3 Расчёт распределения токов в электрической цепи. 1. Постановка задачи Задана электрическая цепь. 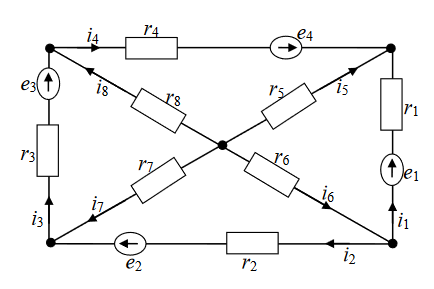 Сопротивления элементов электрической цепи на равны r_k=p+q+k , k=1, 8. Э.д.с. в ветвях цепи равны: e1=2(p+q)+20 ; e2=2(p+q)+3; e3=3(p+q)+8; e4=8(p+q)+39. Числа q, p задаются числовым вариантом студента . Найти распределение токов i_k, k=1,8 ветвях цепи с использованием балансовой модели Кирхгофа. Пусть в качестве источников э.д.с. используются аккумуляторы, причем при их полной зарядке напряжения на них равны e1, e2, e3, e4. Предположим, что в результате эксплуатации аккумуляторы частично разряжаются. При этом напряжения на первых трех доступно для изменения и составляет 80 % от первоначальных значений, т.е 0,8e_k, k=1,3. Напряжение на четвертом аккумуляторе недоступно для измерения. Пусть амперметром измерен ток i1, величина которого оказалась равной 80 % от значения этого тока при полной зарядке всех аккумуляторов. Чему равно напряжение на частично разряженном четвертом аккумуляторе. Можно ли, измеряя ток i1 и напряжение на первых трех аккумуляторах во всех случаях, находить напряжение на четвертом. 2. Ход работы: 3.1 Задача 1 Рассмотрим процесс решения задачи для случая p=0 и q=3. Будем решать систему уравнений , которая для нашего случая имеет вид: I1+i4+i5=0 I1-5i5+6i6=24 -i1-i2+i6=0 2i2+6i6-7i7=7 I2-i3+i7=0 i3+7i7-8i8=14 I3-i4+i8=0 i4-5i5+8i8=55 Систему будем решать матричным методом. Организуем вычислительную область на листе Excel. 3.2 Решение В ячейках А1:J5 запишем исходные данные задачи. Для этого организуем таблицу значений сопротивлений и э.д.с. электрической схемы: 1) строка с номерами «k» вводится как автоматизированный список; 2) строка «r_k» содержит значения сопротивлений. Для рассматриваемой задачи (p=0 и q=3) при вводе сопротивлений можно воспользоваться формулой В4=В3, которую распространяем на диапазон В4:I4; 3) строка «е_k» содержит значения э.д.с. Для рассматриваемой задачи вводим значения: В5>20, С5>3, D5>8, E>39. Далее зададим коэффициенты системы уравнений. Для обеспечения наглядности и упрощения ввода исходных данных оформим матрицу коэффициентов как таблицу, обозначив строки номерами уравнений (А8:А15), а столбцы – указав неизвестные, которые им соответствуют (В7:I7). Далее, зададим значения коэффициентов. Для первых четырех строк, в которых присутствуют токи, расставим на соответствующие места числа 0, 1 и (–1). Для пятого – восьмого уравнений укажем нулевые элементы и ненулевые. 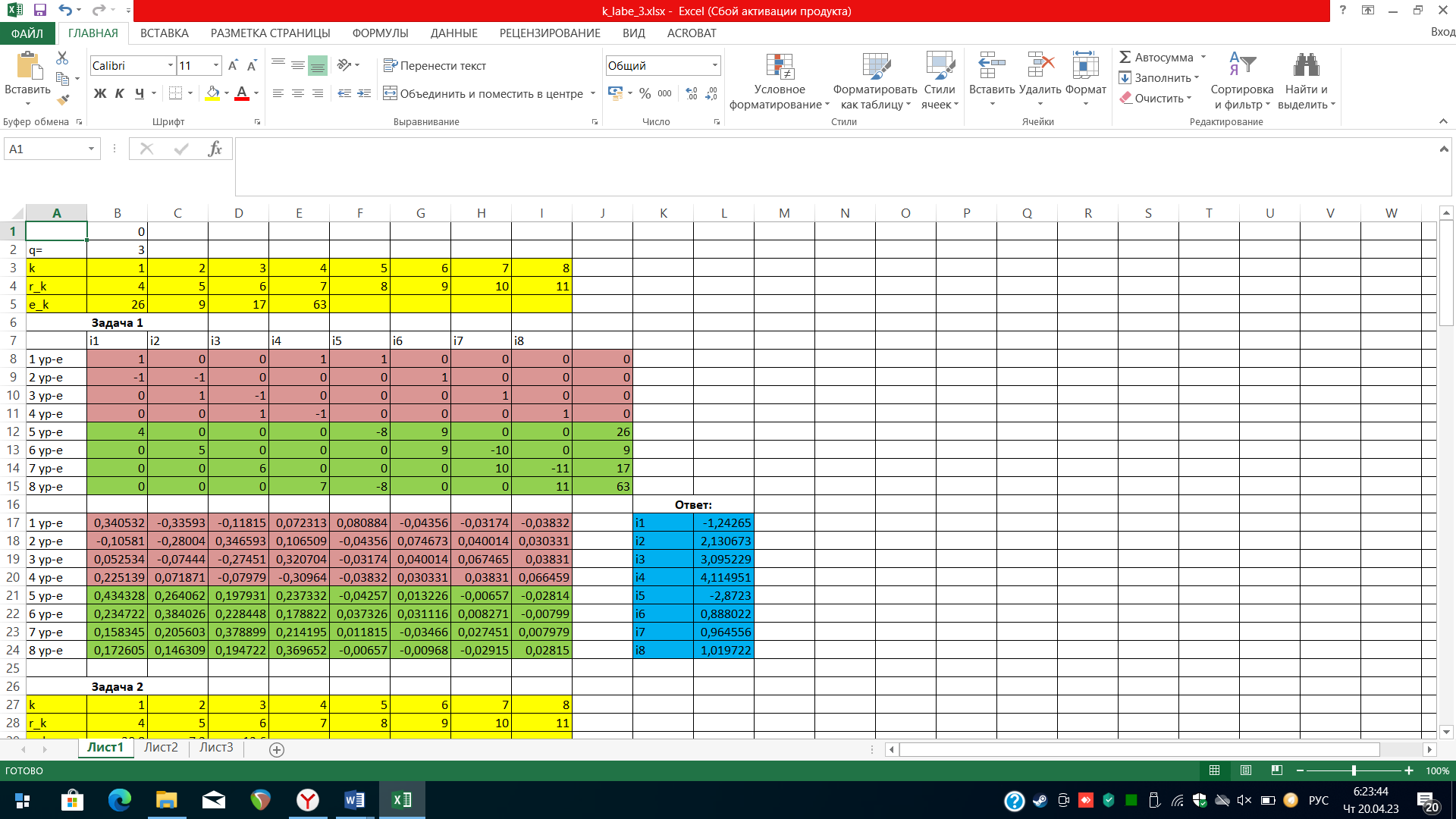 Для последних воспользуемся формулами: В12 > =В4; F12 > =-F4; G6 > =G4; J12 > =B5; C13 >=C4; G13> =G4; H13> =-H4; J13>=C5; D14 > =D4; H14> =H4; I14>=-I4; J14>=D5; E15>=E4; F15>=-F4; I15> =I4; J1>=E5. Для решения системы матричным методом потребуется найти обратную матрицу, поэтому: 1) скопируем диапазон А8:А15 в область А17:А24; 2) запишем формулу в ячейку В17=ОБР(B8:I15); 3) выделим диапазон В17:I24, в котором будем размещать обратную матрицу, поместим курсор в строку формул и одновременно нажмем кнопки Ctrl, Shift, Enter. Теперь вычислим искомые токи: 1) укажем номера вычисляемых токов. Для этого в ячейку K17> i1 и, используя маркер автозаполнения, заполним диапазон K17:K24; 2) теперь умножим полученную обратную матрицу на столбец свободных членов исходной системы уравнений. Запишем формулу в ячейку L17> =УМНОЖ(B17:I24;J8:J15), выделим диапазон L17:L24, поместим курсор в строку формул и одновременно нажмем кнопки Ctrl, Shift, Enter. Вывод: Среди получившихся значений токов оказались как отрицательные, так и положительные. При этом отрицательные значения соответствуют случаю, когда при указании токов в цепи не угадали направление «течения» тока. 4.Задача 2 Напряжения на первых трех источниках составляет 80 % от первоначальных значений и ток i1 оказался равным 80 % от значения этого тока при полной зарядке всех аккумуляторов. Требуется найти напряжение на частично разряженном четвертом аккумуляторе. Преобразуем прошлую систему уравнений так, чтобы неизвестными были токи ik, k 2-8 и э.д.с. e4 : I4+i5=-i1 -5i5+6i6=24*0.8-i1*0.8 -i2+i6=i1 2i2+6i6-7i7=7*0.8 I2-i3+i7=0 3i3+7i7-8i8=14*0.8 I3-i4+i8=0 4i4-5i5+8i8-e4=0 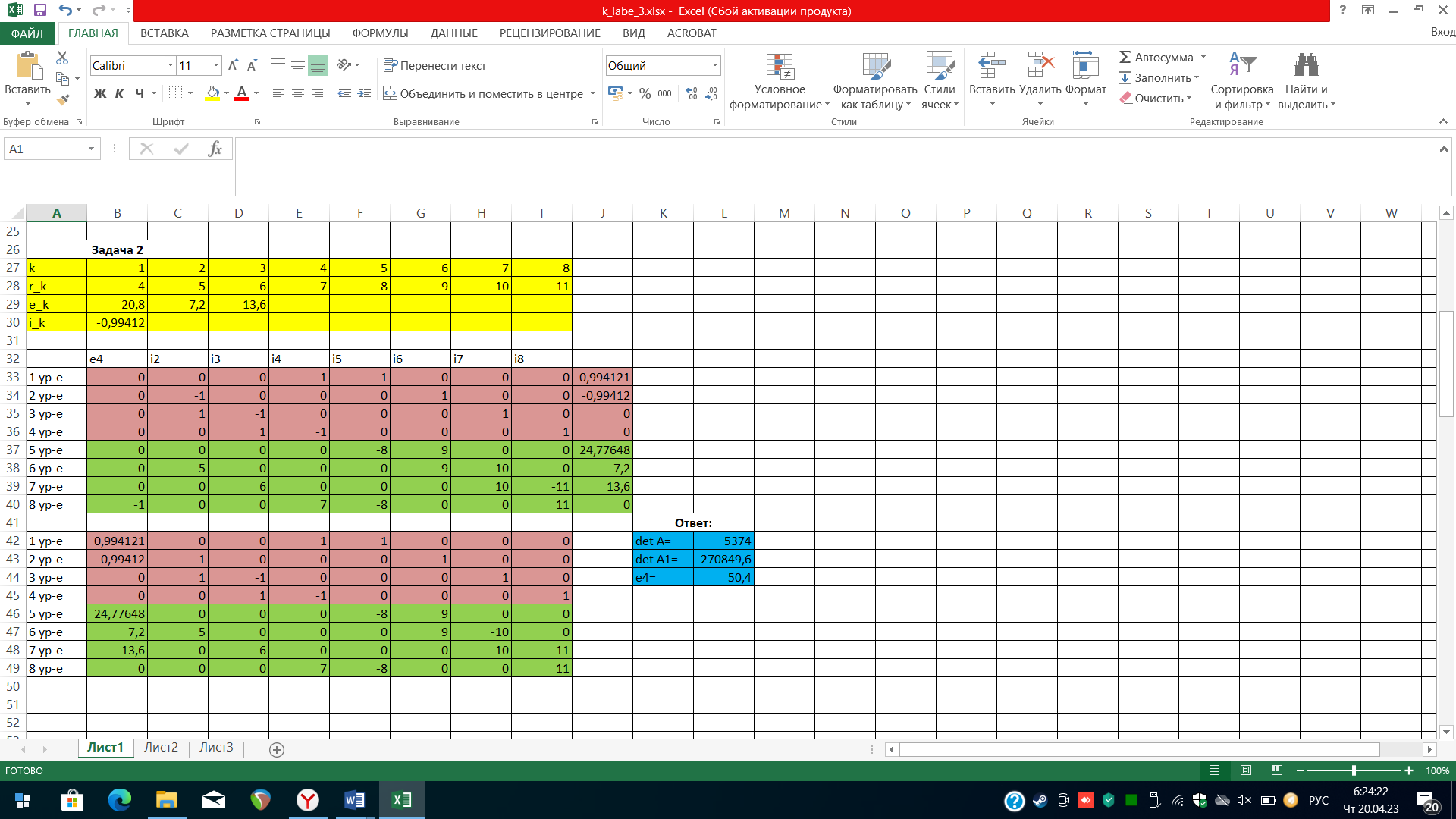 Копируем диапазон А3:I4 в область А27:I28. Значения э.д.с. посчитаем с учетом условий: В29=0,8*B5. Формулу распространим на ячейки С29 и D29. Посчитаем также ток i1 : В30 =0,8*L17. Теперь введем коэффициенты матрицы системы уравнений (3.7). Заметим, что столбцы матрицы соответствующие неизвестным токам ik , k 2-8 не изменятся, тогда можно скопировать диапазон С8:I15 в диапазон С33:I40 с помощью формулы. Выполним это следующим образом: 1) С33=C8; 2) используя маркер автозаполнения, распространим формулу на диапазон С33:I40. Первый столбец формируемой матрицы будет соответствовать неизвестной 4 e , которая встречается только в восьмом уравнении, поэтому введем коэффициенты в диапазон В33:В40. Далее сформируем столбец свободных членов в соответствии с системой (3.7): J33 =-B30; J34 =B30; J35 0; J36 0; J37 =B29-B28*B30; J38 =C29; J39 =D29; J40 0. Решим систему, используя метод Крамера. Учитывая, что требуется найти только e4 , сформируем вспомогательную матрицу для определения e4 , то есть скопируем диапазон С33:I40 в область С42:I49, скопируем диапазон J33:J40 в область В42:В49. Теперь воспользуемся функцией нахождения определителя: L42 =МОПРЕД(B33:I40); L43=МОПРЕД(B42:I49). 5.Вывод: Согласно методу Крамера получаем значение e4 : L44 =L43/L42. Убедимся, что оно составляет 80 % от заданного по условиям задачи. Умножая исходное значение э.д.с. для четвертого источника на 80 %, получаем: 50.4
|
