электротехника. Отчет лабораторной работы 3 (5 вариант). Лабораторная работа 3 Резонанс в электрической цепи синусоидального тока

• Название: Лабораторная работа 3 Резонанс в электрической цепи синусоидального тока
• Анкор: электротехника
• Дата: 13.11.2022
• Размер: 0.77 Mb.
• Имя файла: Отчет лабораторной работы 3 (5 вариант).docx
• Тип: Лабораторная работа; #786168

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

РОССИЙСКИЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

ИМЕНИ Д.И.МЕНДЕЛЕЕВА

Кафедра электротехники и электроники

Лабораторная работа №3

Резонанс в электрической цепи синусоидального тока.

Вариант №5

Выполнили: Канашина Софья, Дурягина Полина, Папугина Алина

Группа: Н-27

Проверил: Илья Алексеевич Ситников

Москва

2022

Лабораторная работа №3

Цель работы: Исследование явления резонанса при последовательном и параллельном соединении элементов R, L, C, определение параметров электрической цепи, установление условий возникновения резонанса напряжений и токов двумя методами:

1. 
   Экспериментальный – имитационное моделирование в среде MultiSim.
   
2. 
   Расчетный – математическое моделирование в любой среде, например: приложения MathCad, Excel и другие, включая расчет на калькуляторе.
   

Начальные данные:

RНом, Ом 25

LНом, мГн 97

CНом, мкФ 88

Ход работы.

Построили цепь, с последовательным соединением элементов R, L, C.

Установили номинальные значения параметров ЭЦ в соответствии с заданным вариантом. Для всех вариантов параметры ЭДС источника: E = 220 В, f = 50 Гц. Выполнили исследование последовательного колебательного контура при изменении емкости конденсатора С и заполнить табл. 3.2. Измерения выполнили в MultiSim.

С_РН=1/(4п²*L*f²)=1/(4*3.14²*97*10^-3*50²)=104,455 мкФ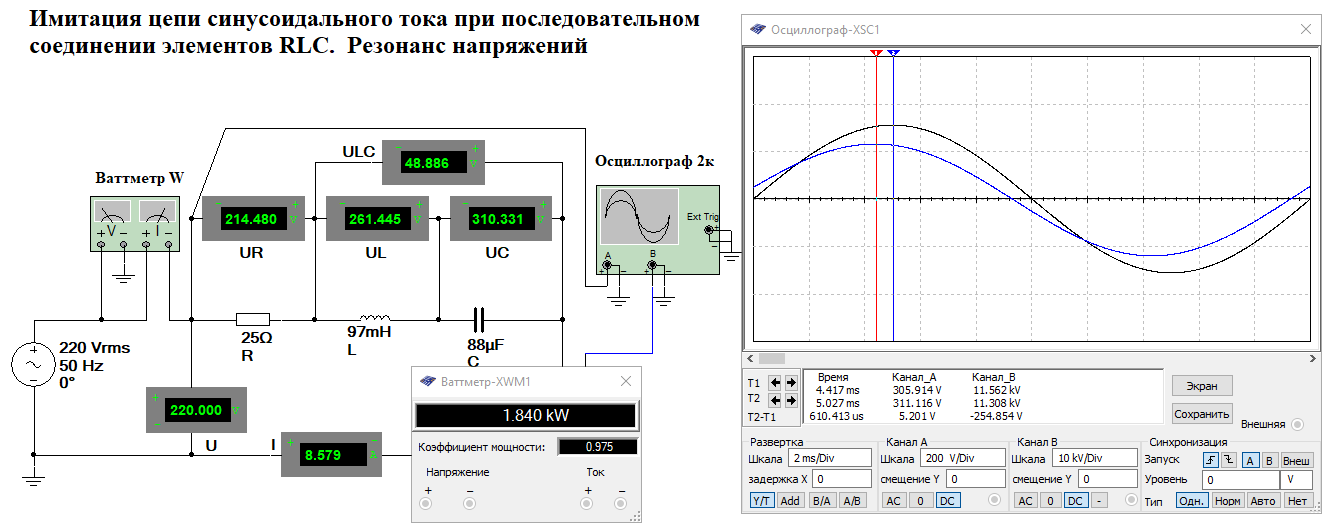

XL

XC

Z

S

Q

cosφ

Расчитать

и заполнить табл. 3.2

Xl=Ul/I Xc=Uc/I Z=U/I S=U*I Q=I^2*(Xl-Xc) cosφ=P/S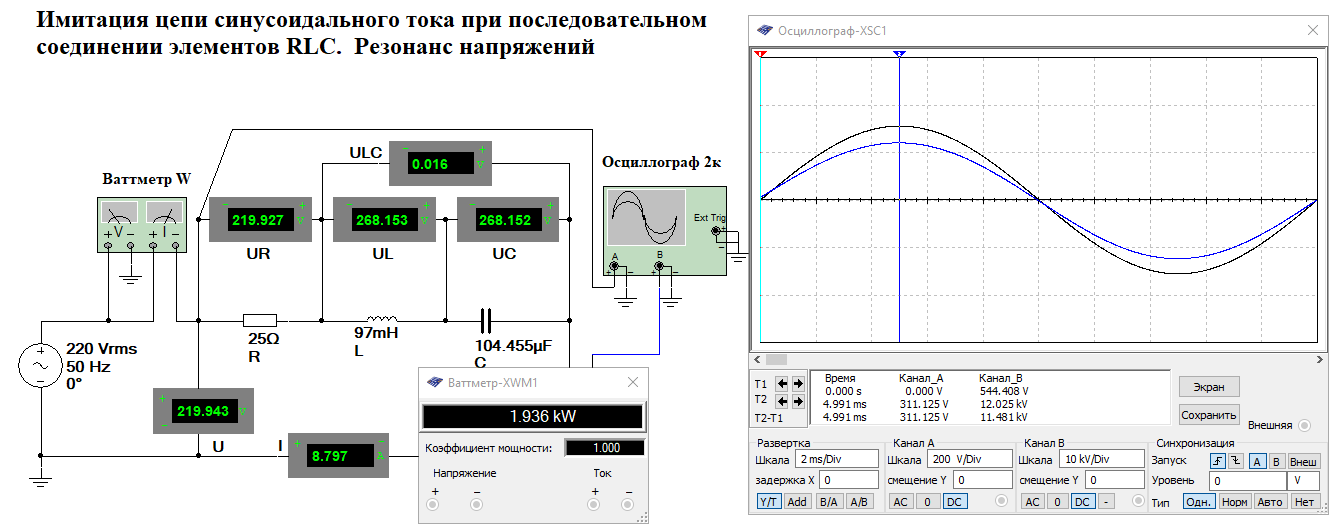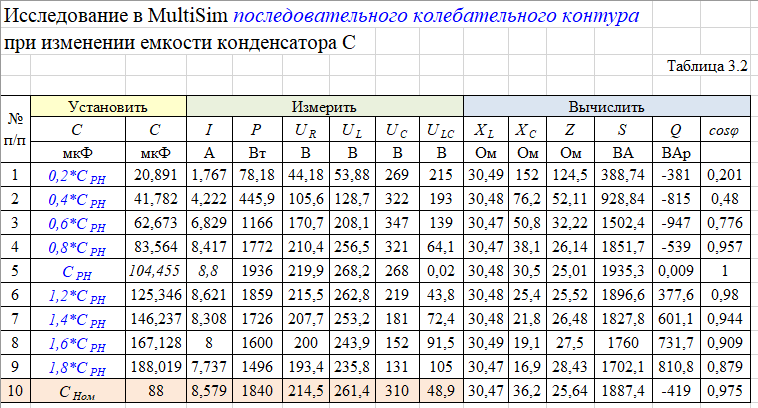





По результатам измерений построили на одном поле графики U_R(С), U_L(С), U_C(С), U_LC(С) и отдельно – I(С).По результатам вычислений построили на одном поле графики X_L(С), X_C(С), Z(С) и на одном полеφ(С) иcosφ(С). Построили на одном поле графики P(С), Q(С), S(С).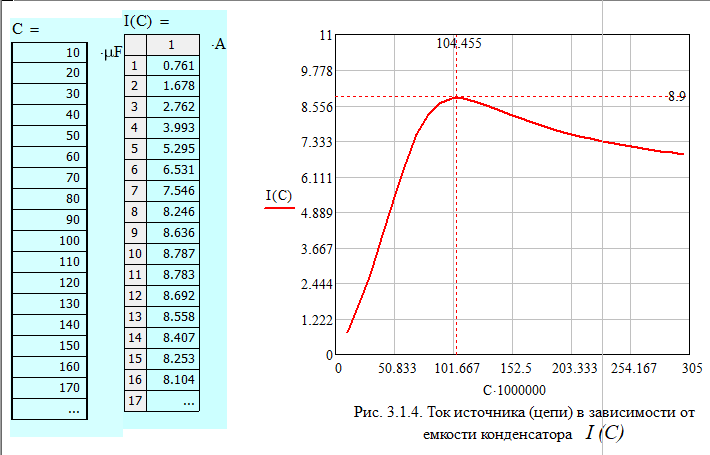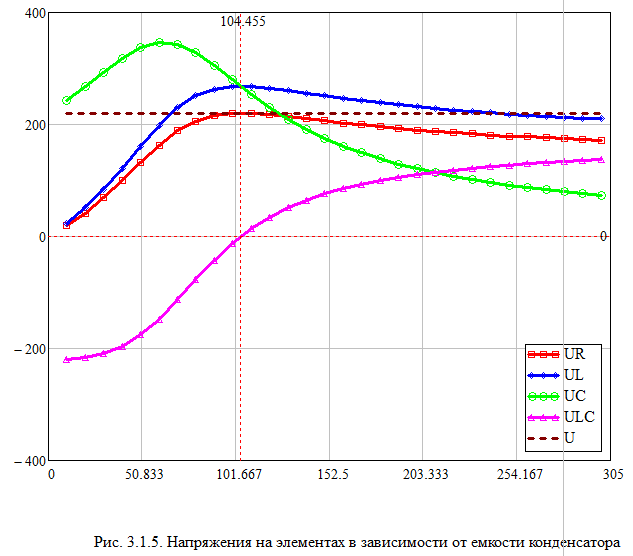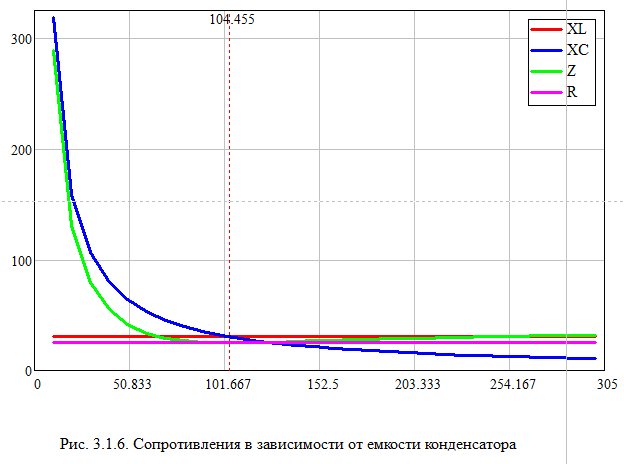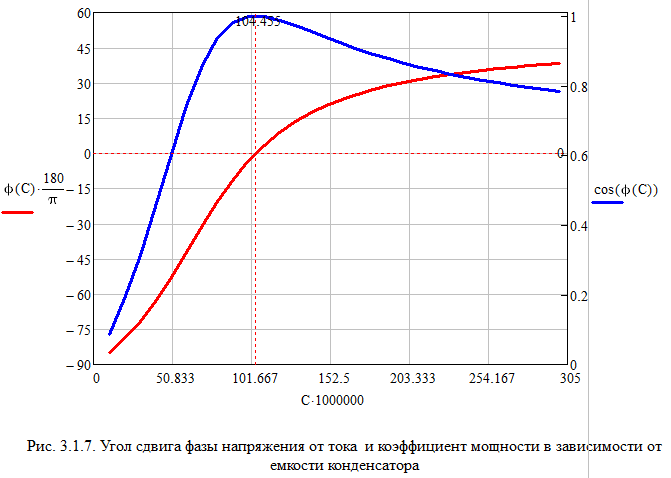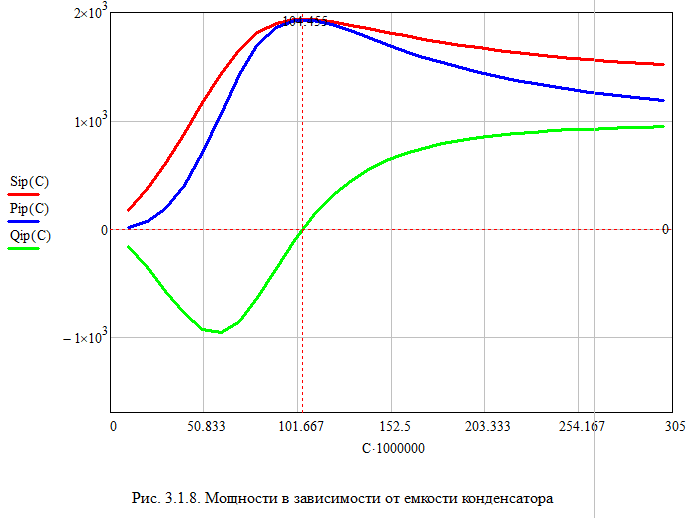









Определили графически резонансную ёмкость конденсатора С^*_РН=104,5 мкФ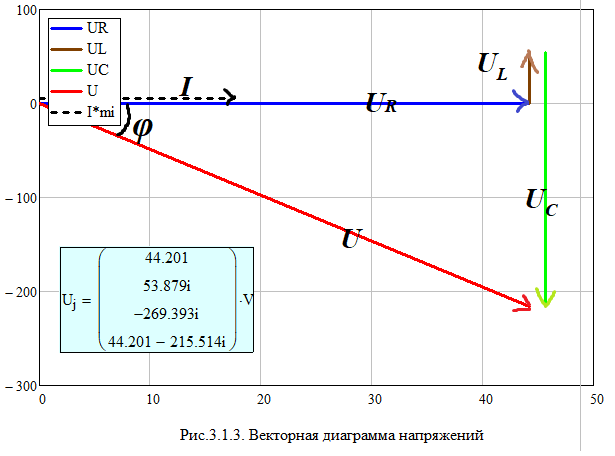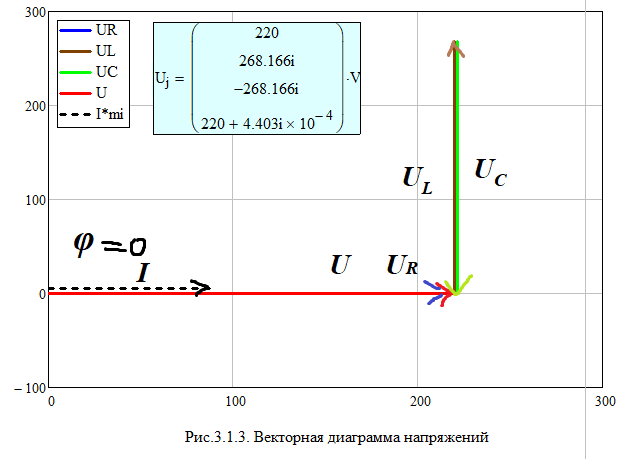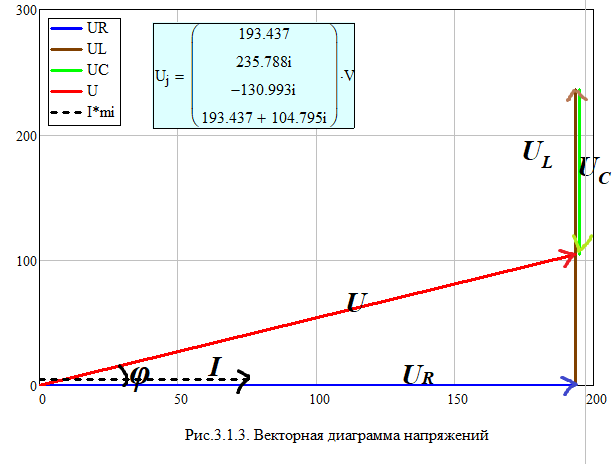







Вычислили добротность контура Q=1,219. Вычислили полосу пропускания контура ΔC=85,693 мкФ

Начальные данные:

RНом, Ом 105

LНом, мГн 97

CНом, мкФ 88

Собрали в MultiSim схему электрической цепи с параллельным соединением элементов R, L,C.Выполнить исследование параллельного колебательного контура при изменении емкости конденсатора С и заполнить табл. 3.4. Измерения выполнить в MultiSim. Cрн=104,455 мкФ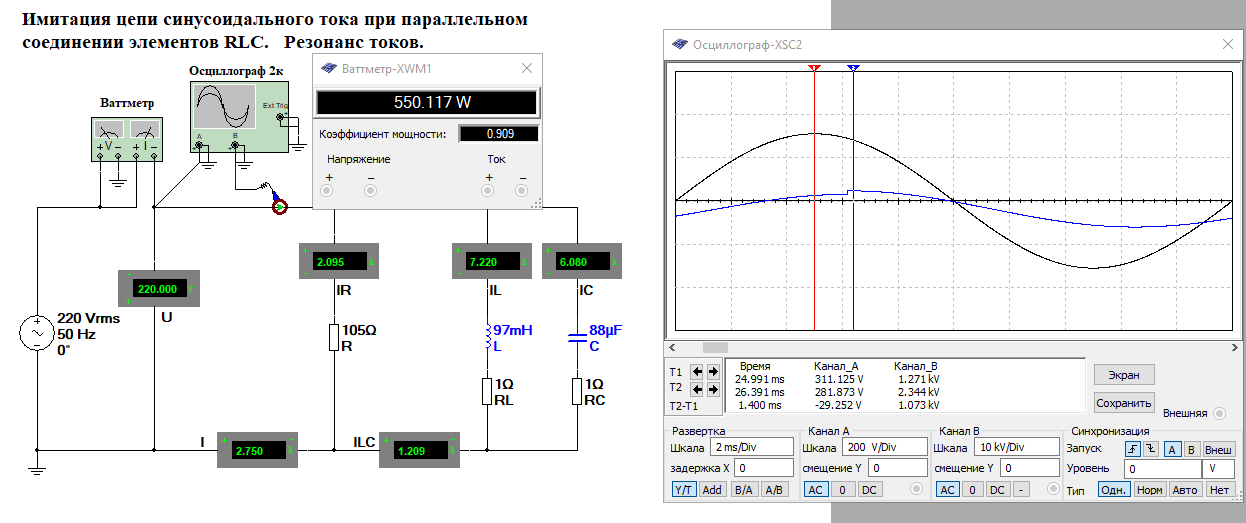



Расчитать Bl, Bc, Y, S, Q, cos(fi) и заполнить табл. 3.5

Bl=1/Xl Bc=1/Xc Y=1/R+(Bc-Bl) S=I*U Q=I^2*(Bc-Bl)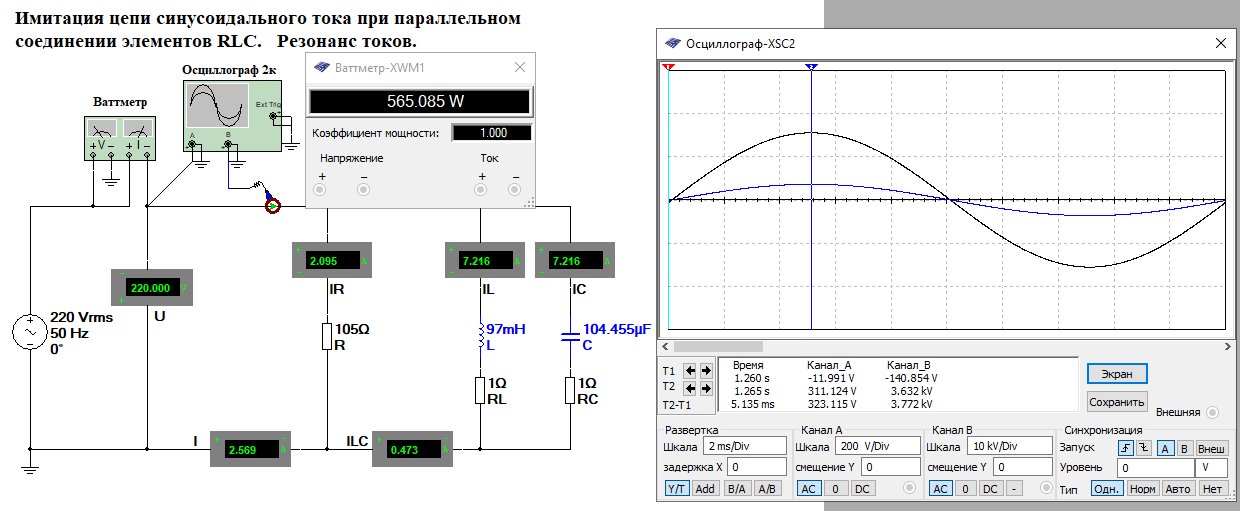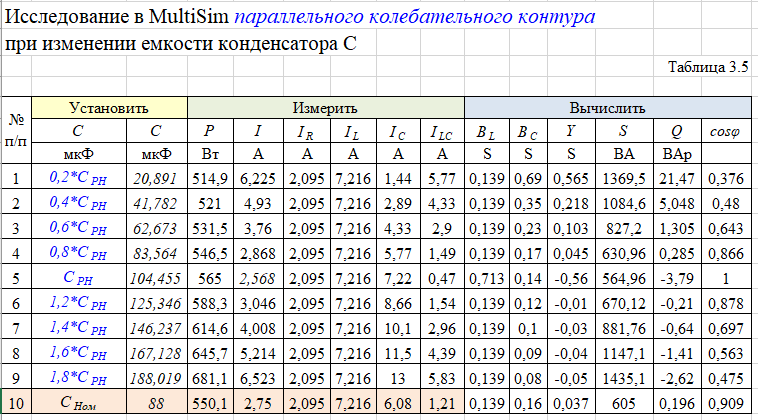





По результатам измерений построили на одном поле графикиI(С), I_R(С), I_L(С), I_C(С), I_LC(С). По результатам вычислений построили на одном поле графики B_L(C), B_C(C), Y(С) и на одном полеφ(С) иcosφ(С). Построили на одном поле графики P(С), Q(С), S(С).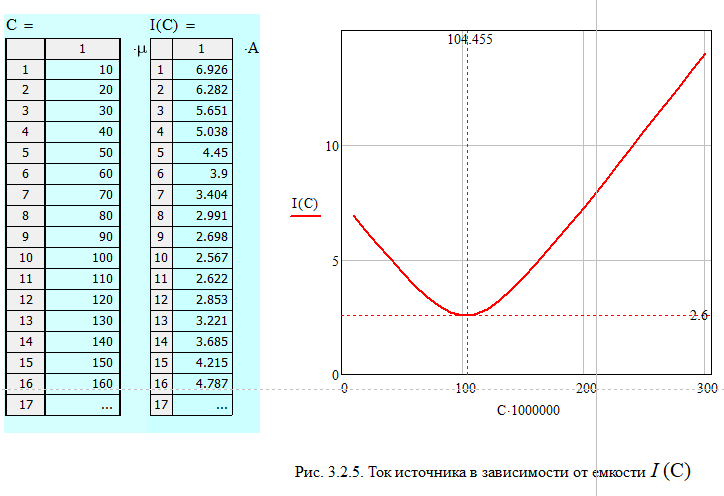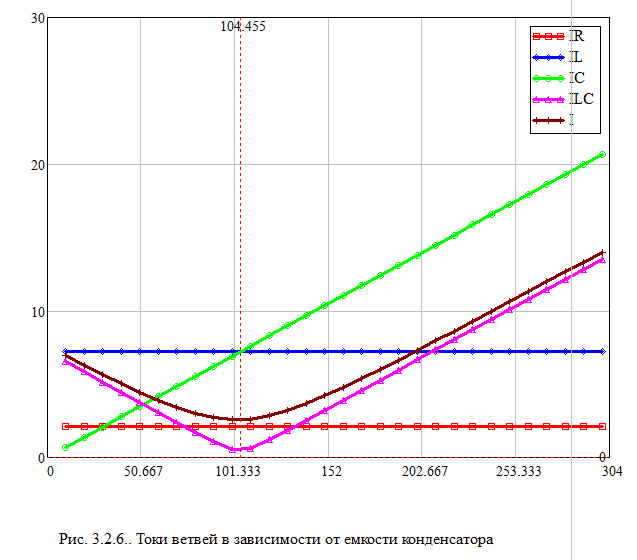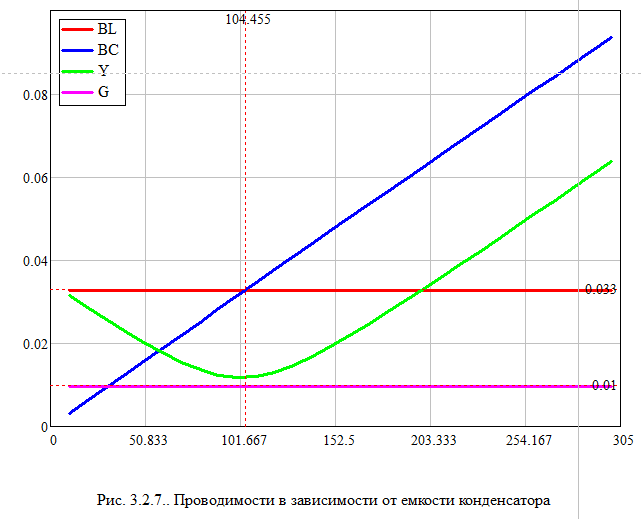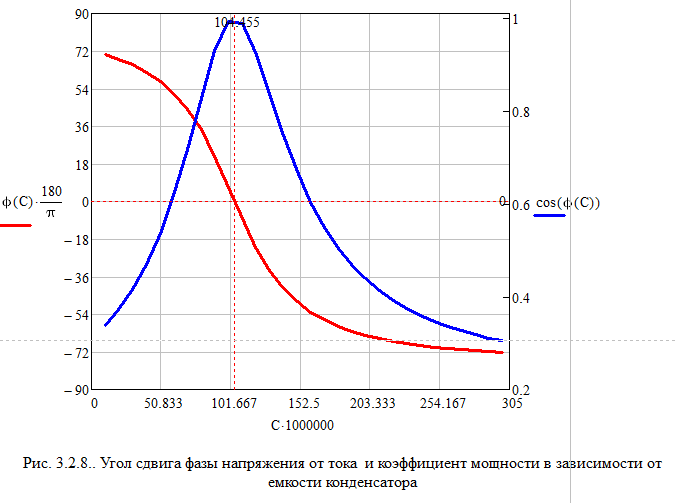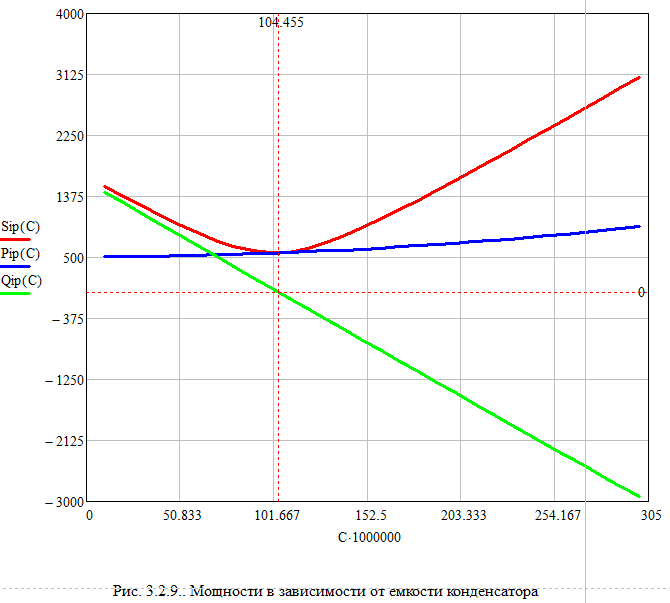







Определили графически резонансную ёмкость конденсатора С^*_РТ=104,5 мкФ

Вычислили резонансную ёмкость конденсатора С_РТ=104,455 мкФ. Вычислили добротность контура Q=2,808. Вычислили полосу пропускания контура ΔC=37,203 мкФ_.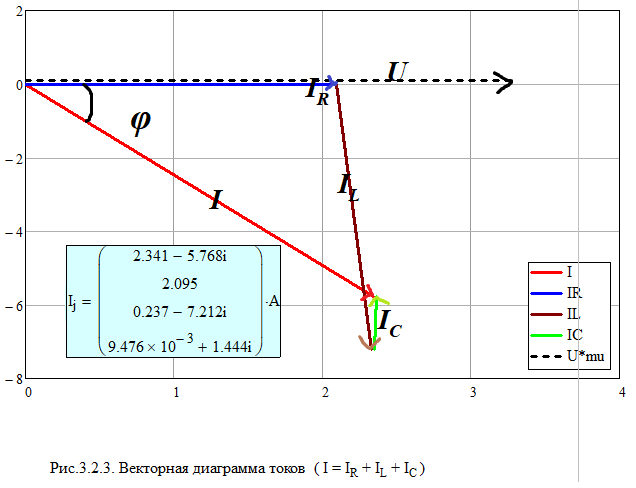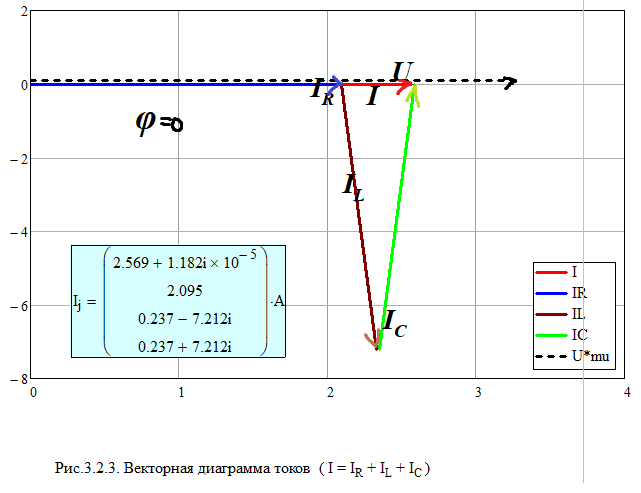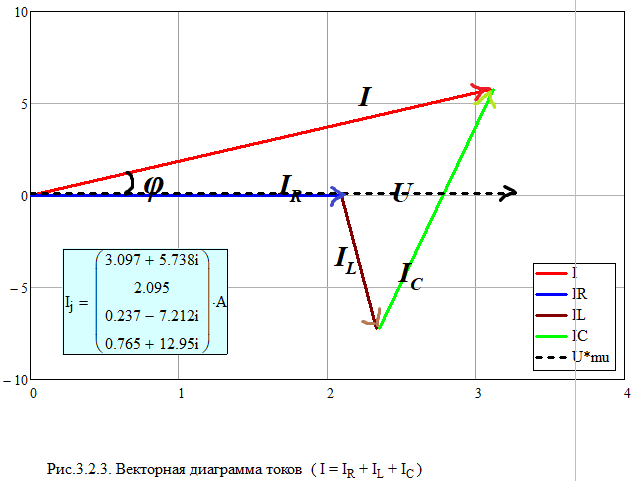





Выводы:

• 
  В программе Multisim мы собрали электрическую цепь, установили значения всех токов, падения напряжений и мощности потребителей. Для исследования резонанса использовали последовательный и параллельный способы соединения R, L и С элементов. Также была использована программа MathCad математического моделирования тех же изменений.
  
• 
  При резонансе сопротивление на катушке XL равно сопротивлению на конденсаторе XC, реактивная мощность Q равна нулю, поэтому, проводимость на катушке индуктивности равна проводимости на конденсаторе, полную мощность S составляет лишь активная P. При параллельном соединении общая реактивная мощность равна нулю.
  
• 
  Проанализировав зависимости сопротивлений, напряжений, тока в ветвях, проводимости, угла сдвига фазы и мощности при изменении емкости конденсатора, можно сказать, что:
  

1) При последовательном соединении R, L, C элементов параметры цепи нелинейно возрастают до максимума (до значения резонанса), и после убывают;

2) При параллельном соединении R, L, C элементов параметры цепи нелинейно убывают, достигая минимума при резонансе, и затем нелинейно возрастают.

В результате данных операций не получится изучить зависимость значений параметров цепи от способа соединения, так как при проведении экспериментов в программе Multisim использовались различные значения сопротивлений.

При резонансной емкости угол сдвига фаз равен нулю, цепь носит чисто активный характер.

В последовательном соединении:

• 
  При уменьшении резонансной ёмкости: угол сдвига фаз меньше нуля, сила тока опережает напряжение, активно-емкостной характер;
  
• 
  При увеличении резонансной ёмкости: угол сдвига фаз больше нуля, напряжение опережает силу тока, активно-индуктивный характер.
  

В параллельном соединении:

• 
  При увеличении резонансной ёмкости: угол сдвига фаз меньше нуля, сила тока опережает напряжение, активно-емкостной характер;
  
• 
  При уменьшении резонансной ёмкости: угол сдвига фаз больше нуля, напряжение опережает силу тока, активно-индуктивный характер.