Системный анализ 3. Задание_3. Лабораторная работа 3. "Сложность и связность систем" Пример Система соединенных проводников с сопротивлениями x 1, x x n
 Скачать 23.31 Kb. Скачать 23.31 Kb.
|
|
Лабораторная работа №3. "Сложность и связность систем" Пример 1. Система соединенных проводников с сопротивлениями x1, x2,..., xn (или химических соединений с концентрациями x1, x2,...,xn реагентов). Поведение этой системы описывается системой линейных алгебраических уравнений:  Заполненность матрицы А (связность) будет отражать сложность системы. Если, например, А - верхнетреугольная матрица, то независимо от n (размерности системы) она легко исследуется на разрешимость. Для этого достаточно выполнить обратный ход метода Гаусса. Если А - общего вида (ни симметрична, ни ленточна и т.д.), то систему сложнее исследовать (необходимо выполнить вычислительно и динамически сложный прямой ход метода Гаусса). Следовательно, система будет обладать структурной сложностью (которая уже может повлечь за собой и вычислительную сложность, например, при нахождении решения). Если число n достаточно велико, то неразрешимость задачи хра-нения матрицы А верхнетреугольного вида в ОЗУ компьютера может стать причиной вычислительной и динамической сложности исходной задачи. Попытка использовать эти данные путём считывания с диска приведет к многократному увеличению времени счета. Пример 2. Упрощение технических средств для работы в сетях, например, достижения, позволяющие подключать компьютер непосредственно "к розетке электрической сети" наблюдается с усложнением самих сетей. Увеличением количества абонентов и информационных потоков в Интернет. Наряду с усложнением Интернет упрощаются (для пользователя!) средства доступа, увеличиваются вычислительные возможности. Пример 3. Рассмотрим множество друзей X={Иванов, Петров, Сидоров} и городов Y={Москва, Париж, Нальчик}. Тогда можно построить 3D-структуру в R3 (в пространстве трёх измерений - высота, ширина, длина), образуемую связыванием элементов X и Y, например, по принципу "кто где был" (рис.). В этой структуре использованы сетевые 2D-структуры X, Y (в которых, в свою очередь использованы 1D-структуры). При этом элементы X и Y можно брать как точки - элементы пространства нулевого измерения - R0. 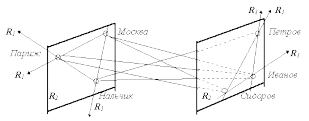 Рис. Геометрическая иллюстрация сложных связных структур. Пример 4. Плохо структурируемы будут проблемы описания многих исторических эпох, проблем микромира, общественных и экономических явлений, например, динамики курса валют на рынке, поведения толпы и др. Пример 5. Аналитичность человеческого знания проявляется и в существовании различных наук, и в дифференциации наук, и в более глубоком изучении все более узких вопросов, каждый из которых сам по себе и интересен, и важен, и необходим. Вместе с тем, столь же необходим и обратный процесс синтеза знаний. Так возникают "пограничные" науки - бионика, биохимия, синергетика и другие. Пример 6. Компьютеризация без постановки новых проблем, т.е. "навешивание компьютеров на старые методы и технологии обработки информации" - это функционирование, а не развитие. Упадок моральных и этических ценностей в обществе могут привести к "функционированию" не только отдельных людей, но и социальных слоев общества. Пример 7. Если на рынке труда будет повышен спрос на квалифицированный труд, появится стремление к росту квалификации, образования, что приведет к появлению новых образовательных услуг, качественно новых форм повышения квалификации. Развитие фирмы, появление сети филиалов может привести к новым организационным формам, в частности, к компьютеризованному офису, виртуальному офису или виртуальной корпорации. Пример 8. В системе ООН для оценки социально - экономического развития стран используют индекс HDI (Human Devolopment Index - индекс развития человечества, человеческого потенциала), который учитывает 4 основных параметра, изменяемых от минимальных до максимальных значений: ожидаемая продолжительность жизни (25-85 лет); уровень неграмотности взрослого населения (0-100 %); средняя продолжительность обучения в школе (0-15 лет); годовой доход на душу населения (200-40000 $). Эти сведения приводятся к общему значению HDI. По HDI все страны делятся на высокоразвитые, среднеразвитые и низкоразвитые. Изменение HDI (параметров, влияющих на него) влияет на экономические и другие параметры. Уровень HDI, наоборот, также может привести к переходу страны из одной категории (развитости по данному критерию) в другую, в частности, если в 1994 году Россия стояла на 34 месте в мире (из 200 стран), то в 1996 году - уже на 57 месте; это приводит к изменениям и во взаимоотношениях с окружающей средой, в том числе, - в политике. Пример 9. Определим сложность иерархической системы как число уровней иерархии. Увеличение сложности при этом требует больших ресурсов для достижения цели. Определим сложность линейной структуры как количество подсистем системы. Определим сложность сетевой структуры как максимальную из сложностей всех линейных структур соответствующих различным стратегиям достижения цели (путей ведущих от начальной подсистемы к конечной). Сложность системы с матричной структурой можно определить количеством подсистем системы. Пример 10. В эколого-экономических системах сложность системы может часто пониматься как сложность эволюции системы, в частности, мера сложности - как мера, функция изменений, происходящих в системе в результате контакта с окружающей средой, её управляемости. Задачи для самостоятельного решения Привести пример одной-двух систем, пояснить причины и тип её сложности, взаимосвязь сложностей различного типа. Указать меры (приемы, процедуры) оценки сложности. Проверить аксиомы сложности. Построить 3D-, 2D-, 1D-структуры сложных систем (комплексов). Сделать рисунки. Привести и описать примеры плохо структурируемых и плохо формализуемых систем, анализа и синтеза таких систем. |
