кпкапк. Лабораторная_работа2_1Эконометрика — копия. Лабораторная работа 2. Корреляционный и регрессионный анализ математический метод оценки взаимосвязей экономических явлений
 Скачать 194.5 Kb. Скачать 194.5 Kb.
|
Лабораторная работа №2. «Корреляционный и регрессионный анализ – математический метод оценки взаимосвязей экономических явлений» Нелинейная регрессия2.1. Методические указанияЧаще всего для оценки взаимосвязей экономических явлений используется линейная функция 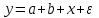 . .В случае, когда между экономическими явлениями существует нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных эконометрических моделей. Линеаризуемы и широко применяются следующие нелинейные уравнения парной регрессии:  - полином 2-й степени; - полином 2-й степени;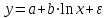 - полулогарифмическая - полулогарифмическая - гипербола; - гипербола;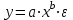 - степенная; - степенная;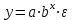 - показательная; - показательная; - экспоненциальная и др. виды функций. - экспоненциальная и др. виды функций. Первые три уравнения (относящиеся к первой группе нелинейных моделей) могут быть легко линеаризованы, путем замены соответствующей нелинейной переменной на линейную. 1. Для полинома 2-й степени  производя замену: производя замену: , ,  получим линейную модель вида  . .2. Для полулогарифмической функции 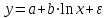 производя замену: производя замену: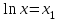 получим линейную модель вида  . .3. 2. Для функции гиперболического вида  производя замену: производя замену:  получим линейную модель вида  . .Аналогично могут быть линеаризованы и другие виды нелинейных функций первой группы (нелинейных по объясняющим переменным, но линейных по параметрам), производя соответствующие замены. Для оценки параметров нелинейных функций первой группы можно использовать, обычный МНК, аналогично, как и в случае линейных функций. Для оценки параметров нелинейных уравнений 4,5,6, которые относятся ко второй группе нелинейных регрессионных моделей (нелинейных по оцениваемым параметрам), также может быть использован метод наименьших квадратов. Для этого нелинейные уравнения второй группы также могут быть приведены к линейному виду. 4. Степенная функция 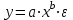 не линейна относительно параметров не линейна относительно параметров 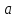 и и 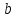 . .Прологарифмировав данную функцию, получим:  или, производя обозначения: или, производя обозначения: , где , где  ; ;  ; ; 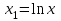 ; ;  . .Применив МНК к полученному уравнению:  , или , или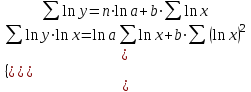 Параметр b определяется непосредственно из системы, а параметр а – косвенным путем: 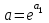 5. Показательная функция  не линейна относительно параметров не линейна относительно параметров 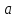 и и 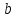 . .Прологарифмировав данную функцию, получим:  или, производя обозначения: или, производя обозначения: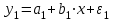 , где , где  ; ;  ; ;  ; ;  . .Применив МНК к полученному уравнению: 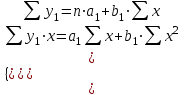 , или , или Параметры 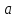 и и 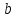 определяются косвенным путем: определяются косвенным путем: 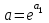 , , 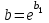 . .6. Экспоненциальная функция  - не линейна относительно параметров - не линейна относительно параметров 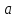 и и 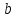 . .Прологарифмировав данную функцию, получим: 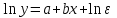 или, производя обозначения: или, производя обозначения: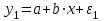 , где , где ; ;  . .Применив МНК к полученному уравнению:  , или , или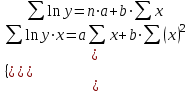 Параметры 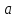 и и 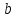 определяются непосредственно из системы. определяются непосредственно из системы.Оценка тесноты корреляционной зависимости в случае нелинейной регрессии производится с помощью индекса корреляции (R)  . .Величина R2 называется индексом детерминации. Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:  , , где R2- индекс детерминации; n - число наблюдений; m - число параметров при переменных х. Чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации: 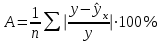 Существует и другая формула определения средней ошибки аппроксимации:  , где , где  . .1.2 Реализация типовых задач на компьютере. Формулировка задачи: По 13 регионам России известны данные за 2014г. (табл. 1): Таблица 1 Основные социально-экономические показатели регионов России
Задание Рассчитайте параметры уравнений линейной, полиномиальной 2-й степени, полулогарифмической, гиперболической, степенной, показательной и экспоненциальной регрессии. Оцените тесноту связи с помощью показателей корреляции и детерминации. Оцените с помощью средней ошибки аппроксимации качество уравнений. Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в п. 3 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование. Оцените полученные результаты, выводы оформите в аналитической записке. Решение с помощью ППП Excel Для оценки параметров приведенных моделей регрессии можно воспользоваться встроенной статистической функцией ЛИНЕЙН, которая определяет параметры линейной регрессии y=a+bx. Порядок вычисления следующий: Введите исходные данные или откройте существующий файл, содержащий анализируемые данные. Выделите область пустых ячеек 5х2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики. Активизируйте Мастер функций любым из способов: а) в главном меню выберите Формулы/Вставить функцию; б) Shift+F3; В окне Категория (рис. 1.1) выберите Статистические, в окне Выберите функцию - ЛИНЕЙН. Щелкните по кнопке ОК; 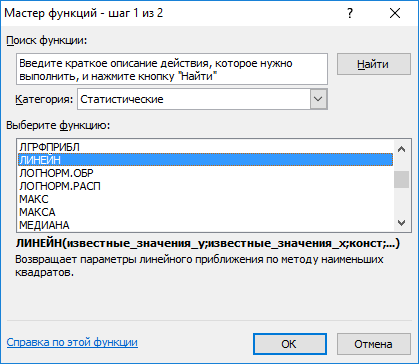 Рис. 1.1. Диалоговое окно «Мастер функций» Заполните аргументы функции (рис. 1.2): Известные_значения_у - диапазон, содержащий данные результативного признака; Известные_значения_х - диапазон, содержащий данные факторов независимого признака; Константа - логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0; Статистика - логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения. Щелкните по кнопке ОК; 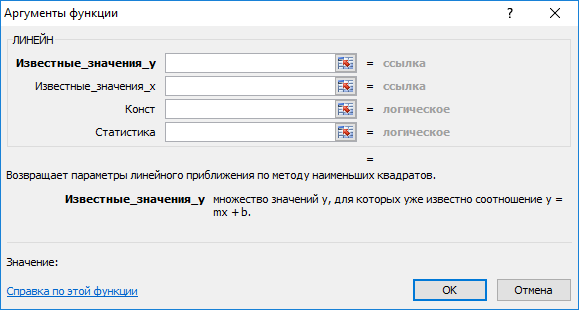 Рис. 1.2. Диалоговое окно ввода аргументов функции ЛИНЕЙН В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
Для вычисления параметров показательной функции 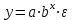 в MS Excel применяется встроенная статистическая функция ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН. в MS Excel применяется встроенная статистическая функция ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН.Для того, чтобы воспользоваться встроенными функциями Excel для оценки параметров и статистических характеристик моделей парной регрессии, необходимо сначала подготовить таблицы с данными. Шаблон для размещения исходных переменных для оценки параметров линейной регрессии и преобразованных переменных для оценки параметров нелинейных регрессий можно представить в виде таблицы 1. Таблица 2 Таблица-шаблон размещения исходных и преобразованных переменных для оценки параметров линейной и нелинейных моделей парной регрессии.
продолжение таблицы 2
Далее необходимо провести расчеты с помощью встроенных статистических функций Excel - ЛИНЕЙН и ЛГРФПРИБЛ. Эти расчеты удобно разместить в виде следующего шаблона (табл. 3). Таблица 3 Таблица-шаблон промежуточных расчетов для оценки параметров и статистических характеристик моделей парной регрессии с помощью встроенных статистических функций Excel - ЛИНЕЙН и ЛГРФПРИБЛ.  В полученных расчетных данных недостаточно информации для расчета индекса корреляции (R) и детерминации (R^2), средней ошибки аппроксимации (Aср) и F -критерия Фишера для степенной, показательной и экспоненциальной моделей. Поэтому необходимы дополнительные расчеты для оценки остаточной и регрессионной суммы квадратов, которые можно представить в виде шаблона (табл.4) Таблица 4 Таблица-шаблон промежуточных расчетов для оценки статистических характеристик второй группы нелинейных моделей парной регрессии.
Результативную таблицу можно представить в виде таблицы 5. Параметры и статистические характеристики для линейной, полиномиальной, полулогарифмической и гиперболической моделей (первая группа нелинейных моделей) в таблицу 5 переносим из соответствующих ячеек таблицы 3, Аср рассчитывается по формуле 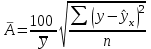 , где , где  , берем из таблицы 3 (среднеквадратическое отклонение Y). , берем из таблицы 3 (среднеквадратическое отклонение Y).Таблица 5 Таблица-шаблон для вывода конечных результатов корреляционно-регрессионного анализа нелинейной регрессии
Для нелинейных моделей второй группы (степенная, показательная и экспоненциальная параметры и характеристики переносим из таблицы 3, или рассчитываем по соответствующим формулам, на основе данных промежуточных расчетов в таблице 3 и 4. При расчете Ryx 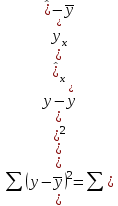 рассчитываем на основе данных таблицы 4. рассчитываем на основе данных таблицы 4. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||