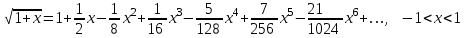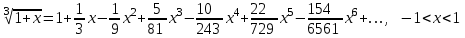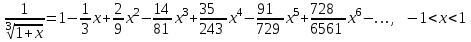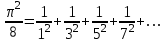лабороторная. Лабороторная 3. Лабораторная работа 3 Тема Оператор цикла for Цели работы
 Скачать 304 Kb. Скачать 304 Kb.
|
|
Лабораторная работа №3 Тема: Оператор цикла for Цели работы: Получение навыков составления алгоритмов и программ обработки последовательностей с помощью оператора цикла for (на примере задачи вычисления суммы ряда с заданным чиcлом слагаемых). Реализация элементарных математических вычислений с использованием операторов языка программирования С#. Организация ввода/вывода и осуществление контроля вводимых данных средствами языка С#. Краткие теоретические сведения. Под циклом понимается многократное выполнение одних и тех же операторов при различных значениях промежуточных данных. Число повторений может быть задано в явной или неявной формах. Для организации повторений в языке C++ используются три различных оператора цикла. Цикл for | for (выражение1; выражение2; выражение3) { Операторы (тело цикла); } | выражение1 (инициализирующее). Задает начальное значение переменной, управляющей циклом (инициализация счётчика цикла); выражение2 задает условие продолжения цикла (как правило, это операция отношения). Если оно возвращает не ноль (истина), то выполняется тело цикла, если возвращает ноль (ложь), то выполняется первый оператор, стоящий за закрывающей цикл фигурной скобкой; выражение3 обеспечивает изменение цикловой переменной (счетчика цикла). Оператор (операторы), стоящий после закрывающей скобки, задает тело цикла. В большинстве случаев телом цикла является блок, т.е. набор операторов, заключенных в {}. Сколько раз будет выполняться тело цикла, зависит от трех управляющих элементов, заданных в круглых скобках. Принцип работы for-цикла: Вычисляется выражение1. Вычисляется выражение2. Если оно истинно (true или не ноль), то выполняется тело цикла (Операторы), после чего вычисляется выражение 3 и см. п.2 сначала. Если ложно – цикл прерывается и управление передается на следующий за циклом оператор. Например:
В указанном примере: i = 0; это инициализация счетчика, i < 10; это условие цикла, i++ это изменение счётчика (добавление 1). Счетчики цикла зачастую объявляются непосредственно в инициализаторе и соответственно являются переменными, локализованными в цикле, так что после завершения цикла они перестают существовать. В тех случаях, когда предусматривается возможность преждевременного завершения цикла с помощью одного из операторов перехода, счетчики объявляются до цикла, что позволяет анализировать их значения при выходе из цикла. ПРИМЕРЫ Пример 1. Найти сумму всех целых чисел от 100 до 200. Фрагмент программы, которая решает данную задачу с использованием цикла for следующий: // вычислить сумму int sum; int i; sum = 0; for (i = 100; i <= 200; i++) sum += i; // sum = 15150 Пример 2. Дано натуральное число n. Разработать программу, которая находит следующую сумму 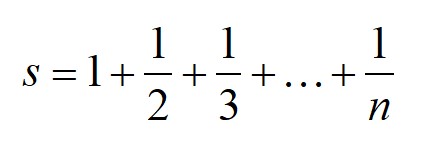 Фрагмент кода, решающий данную задачу / вычислить сумму double sum; int i; int n; n = 10; sum = 0; for (i = 1; i <= n; i++) sum = sum + 1.0 / i; // sum = 2.92896825396825 Пример 3. Рекуррентные соотношения (теорию см. ниже). Последовательность чисел a0, a1, a2, … получается по закону: Дано натуральное число n. Получить a1, a2, …, an. Фрагмент программы, которая решает данную задачу, следующий: { // вычислить a1, a2, ..., an double a0, ak; int k; int n; n = 10; a0 = 1; k = 0; // Вывод на форму или на консоль("a[{0}] = {1}", k, a0); for (k = 1; k <= n; k++) { ak = k * a0 + 1.0 / k; // Вывод на форму или на консоль ("a[{0}] = {1}", k, ak); a0 = ak; } } В результате выполнения вышеприведенного кода, будет выведен следующий результат: a[0] = 1 a[1] = 2 a[2] = 4.5 a[3] = 13.8333333333333 a[4] = 55.5833333333333 a[5] = 278.116666666667 a[6] = 1668.86666666667 a[7] = 11682.2095238095 a[8] = 93457.8011904762 a[9] = 841120.321825397 a[10] = 8411203.31825397 Пример 4. Следующая программа находит произведение цифр от 1 до N (факториал). (здесь – вывод на консоль, вывод на форму не меняет значимой части программы)
Вот один из возможных результатов работы данной программы: Вывод нашей программы N = 7 5040 Process returned 0 (0x0) execution time : 2.723 s Press any key to continue. Теперь приступим к разбору кода: Строка 6: мы создаем переменную n. В будущем ее мы будем использовать в условии выполнения цикла. Строка 10: нам нужна переменная, в которой будет храниться результат работы цикла. Поэтому мы создаем переменную res. Строка 11: добрались до цикла for. Здесь давайте разберемся поподробнее: в качестве счетчика выступает переменная i. Мы сразу ей задаем значение 1 (собственно можно было начать и с двух, поскольку умножение на 1 не имеет смысла); условием выполнения цикла является нестрогое неравенство. Цикл будет выполнятся до тех пор, пока i меньше или равно n; после каждой итерации мы увеличиваем значение счетчика на единицу (операция инкремента). Это равносильно следующей записи: i = i + 1. Строка 14: выводим результат работы программы на экран пользователя. Внимание! При вычислении суммы ряда рекомендуется задавать начальное значение S0=0, тогда это не будет влиять на итоговый результат; а при вычислении произведения начальное значение res = 1 (иначе произведение обнулится). Пример 5. Используя оператор цикла с параметром for найти сумму ряда: 1. Создание проектаЗагрузить MS Visual Studio. Создать проект по шаблону «Windows Forms Application». 2. Размещение элементов управления В соответствии с условием задачи, в программе фигурирует переменная n, которую нужно ввести с клавиатуры. Поэтому, форма программы будет иметь вид, как изображено на рисунке 1. На форме размещаются следующие элементы управления: два элемента управления типа Label с именами label1 и label2; элемент управления типа Button с именем button1; элемент управления типа TextBox с именем textBox1. 3. Настройка свойств элементов управления В элементах управления настроить следующие свойства: в элементе управления label1 свойство Text = «n =»; в button1 свойство Text = «Вычислить»; в Form1 свойство Text = «Сумма ряда«; в label2 свойство Text = «Сумма ряда =». После настройки, форма программы примет вид как показано на рисунке 1. 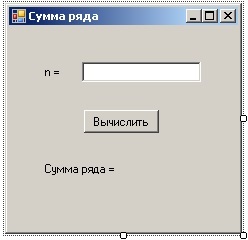 Рисунок 1. Главная форма программы 4. Программирование события клика на кнопке «Вычислить«При клике на кнопке «Вычислить» будет проводиться расчет суммы ряда. В этом случае нужно запрограммировать событие Click элемента управления button1. Подробный пример программирования события Click описывается здесь. Листинг (фрагмент) следующий: { double summa; int i, n; // ввод значения n n = Convert.Toint32(textBox1.Text); // вычисление суммы summa = 0; for (i=1; i<=n; i++) summa = summa + 1.0/i; // вывод результата на экран label2.Text = "Сумма ряда = " + summa.ToString(); } Возможные ошибкиЦикл — это одновременно очень удобный инструмент для работы, но в тоже время он таит немало скрытых угроз. Неопытные программисты могут совершать ошибки, которые не просто выявить, поскольку программа успешно компилируется и начинает работу. СегфолтУ данной ошибки довольно много причин. В случае работы с циклами она может возникнуть следующим образом:
Вы могли заметь, что здесь переменной i не задали значение. Изначально переменная содержит «мусор» (можете вывести такой мусор на экран для того, чтобы понять о чем говорится). Естественно, к мусору прибавлять ничего нельзя — программа может вылететь. Постарайтесь выработать привычку всегда обнулять созданные переменные. Это избавит вас от огромного количества проблем при написании программ. Некоторые компиляторы обнуляют переменные при их создании. Например, это делает компилятор gcc. Бесконечный циклДанная ошибка часто возникает из-за неправильного условия или изменение значения счетчика внутри цикла. Посмотрим на простой пример:
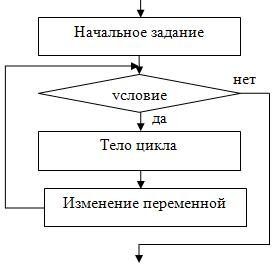
Данный цикл никогда не завершится, поскольку внутри значение i уменьшается на единицу, а после опять увеличивается. Таким образом, условие i < 10 всегда будет истинным. Программа «зависнет». Рекуррентная формула При суммировании ряда необходимо, как правило, решить следующие задачи: свести вычисления к простейшим арифметическим операциям; уменьшить число этих операций и время расчета; уменьшить погрешность округления. Рассмотрим вычисление функции sin x. Разложение этой функции в ряд Тейлора имеет следующий вид Область сходимости ряда определяется неравенством Величина n! называется «n-факториал» и вычисляется по формуле: n! = 1×2×3×…×(n– 1)× n = (n– 1)!×n или Принято считать, что 0! = 1. Суммирование ряда последовательным вычислением слагаемых и добавлением их к сумме, как в приведенном выше примере, сводит вычисления к простейшим арифметическим операциям, то есть первая задача при этом решается. Что касается второй задачи – уменьшения количества этих операций, – то многократное перемножение чисел в числителе (степени x) и в знаменателе (n!) вряд ли можно считать рациональным. При этом (третья задача) погрешность вычислений возрастает с увеличением номера члена ряда – слишком велики становятся и числитель, и знаменатель. Задачи сокращения количества операций и уменьшения погрешности вычислений решает рекуррентная формула, позволяющая вычислить значение очередного члена ряда, используя уже найденное значение предыдущего. Рекуррентная формула имеет вид: an+1 = an × Tn, где Tn – коэффициент рекурсии. В нашем примере произвольный член ряда определяется формулой: Номер начального члена ряда n = 0, его значение a0 = x. Для расчета коэффициента рекурсии определим значение следующего (n+1)-го члена ряда. В формулу общего члена ряда вместо n подставим (n+1), получим 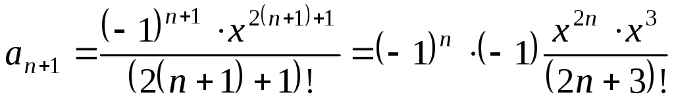 Вычисляя коэффициент рекурсии, сокращаем дробь: Чтобы сократить факториалы, рассмотрим числитель и знаменатель отдельно: (2n + 1)! = 1 × 2 × 3 × … × (2n + 1) (2n + 3)! = 1 × 2 × 3 × … × (2n + 1) × (2n + 2) × (2n + 3) Окончательная формула коэффициента рекурсии Отсюда получаем рекуррентную формулу для вычисления членов ряда Проверка полученной формулы убережет Вас от ошибок в алгоритме и, возможно, сэкономит усилия при отладке программы. Подставив n = 0 в формулу общего члена ряда Далее определим по рекуррентной формуле a1 и a2, сверяя результаты с соответствующими членами ряда: при n = 0 при n = 1 Совпадение полученных значений с членами ряда показывает, что коэффициент рекурсии рассчитан правильно. ЗАДАНИЕ. ВЫЧИСЛЕНИЕ СУММЫ РЯДА Даны действительное число x, (x≠0), целое число n. Составить программу и вычислить сумму ряда S (вариант задания выбирается по номеру в списке группы – см. ниже). Ход работы Провести анализ элемента ряда. Составить рекуррентную формулу для вычисления элемента ряда. Составить алгоритм решения задачи. Запрограммировать алгоритм на языке С#. Провести тестирование программы на нескольких примерах (для n = 10 и n =20; х= 0,1; х= 9,9; х= 99,1) – всего 6 тестов. Если в варианте задания указаны ограничения для х, то самостоятельно подобрать 3 значения х. Внимание! При некоторых значениях входных данных возможно отсутствие решения (например, при переполнении памяти). В этих случаях привести в отчете скриншот с сообщением (диагностикой). Содержание отчета Задание. Постановка задачи Формулировка задачи (с учетом варианта задания); Входные данные - указать имена переменных и их типы; Ограничения на входные данные; Выходные данные (результаты) - указать имена переменных и их типы; Дополнительные данные (промежуточные переменные) - указать имена переменных и их типы, а также комментарии относительно назначения переменных. Метод решения задачи (математическая модель, рекуррентная формула). Листинг программы на языке С# (можно - скриншот), обязательно – с подробными комментариями. 6 тестовых примеров, демонстрирующих результаты работы программы (можно – в табличной форме). Cкриншот 1 варианта формы с результатами. Выводы (влияние входных данных на результат) Варианты заданий:  Варианты заданий (в заданиях К – очередной член ряда)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

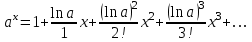
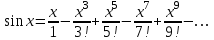
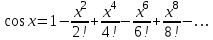
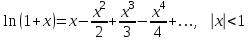
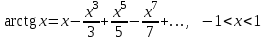
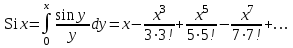
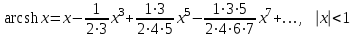
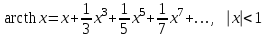
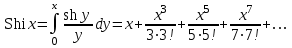
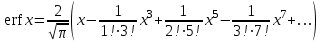 Интеграл вероятностей
Интеграл вероятностей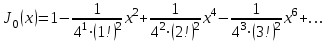 Функция Бесселя
Функция Бесселя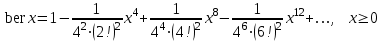 Функция Кельвина
Функция Кельвина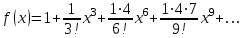 Функция Эйри
Функция Эйри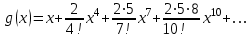 Функция Эйри
Функция Эйри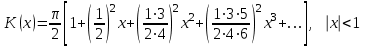 Эллиптич.интеграл
Эллиптич.интеграл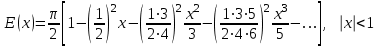 Эллиптич.интеграл
Эллиптич.интеграл