Лаба 31. Лабораторная работа 31 Исследование электростатического поля методом электролитической ванны Выполнила студентка группы о23

• Название: Лабораторная работа 31 Исследование электростатического поля методом электролитической ванны Выполнила студентка группы о23
• Дата: 10.05.2022
• Размер: 312.5 Kb.
• Имя файла: Лаба 31.doc
• Тип: Лабораторная работа; #520643

Лабораторная работа № 31

«Исследование электростатического поля

методом электролитической ванны»
Выполнила студентка группы О-23 Бакулина Мария
Цель работы – экспериментальное изучение электростатического поля цилиндрического конденсатора на модели; подтверждение теоремы Остроградского-Гаусса.
Приборы и принадлежности: источник питания – звуковой генератор, измерительный прибор – ламповый вольтметр с зондом, электролитическая ванна, два металлических электрода, стеклянная платина, соединительные провода.
С
ламповый вольтметр

звуковой генератор

ванна

электроды

шкалы

зонд
хема установки – см. рисунок.

Таблица результатов измерений потенциалов (таблица 1):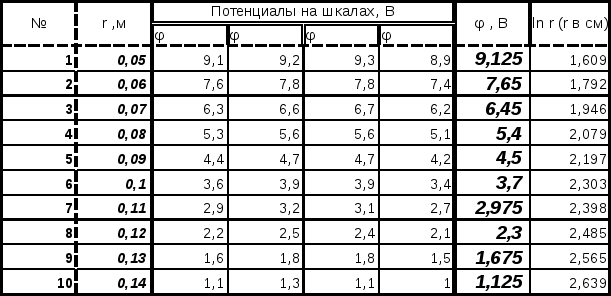




Обработка результатов измерений:

1. 
   Средние значения φ_i:
   

φ_i=1/n∙∑φ_ik

См. 7-й столбец таблицы 1.

2. 
   Абсолютная погрешность Δφ_ik каждого измерения:
   

Δφ_ik= φ_i - φ_ik

Δφ₁₁= φ₁ – φ₁₁ = -0.025

Δφ₁₂= φ₁ – φ₁₂ = 0.075

Δφ₁₃= φ₁ – φ₁₃ = 0.175

Δφ₁₄= φ₁ – φ₁₄ = -0.225

Δφ₂₁= φ₂ – φ₂₁ = -0.05

Δφ₂₂= φ₂ – φ₂₂ = 0.15

Δφ₂₃= φ₂ – φ₂₃ = 0.15

Δφ₂₄= φ₂ – φ₂₄ = -0.25

Δφ₃₁= φ₃ – φ₃₁ = -0.15

Δφ₃₂= φ₃ – φ₃₂ = 0.15

Δφ₃₃= φ₃ – φ₃₃ = 0.25

Δφ₃₄= φ₃ – φ₃₄ = -0.25

Δφ₄₁= φ₄ – φ₄₁ = -0.1

Δφ₄₂= φ₄ – φ₄₂ = 0.2

Δφ₄₃= φ₄ – φ₄₃ = 0.2

Δφ₄₄= φ₄ – φ₄₄ = -0.3

Δφ₅₁= φ₅ – φ₅₁ = -0.1

Δφ₅₂= φ₅ – φ₅₂ = 0.2

Δφ₅₃= φ₅ – φ₅₃ = 0.2

Δφ₅₄= φ₅ – φ₅₄ = -0.3

Δφ₆₁= φ₆ – φ₆₁ = -0.1

Δφ₆₂= φ₆ – φ₆₂ = 0.2

Δφ₆₃= φ₆ – φ₆₃ = 0.2

Δφ₆₄= φ₆ – φ₆₄ = -0.3

Δφ₇₁= φ₇ – φ₇₁ = -0.075

Δφ₇₂= φ₇ – φ₇₂ = 0.225

Δφ₇₃= φ₇ – φ₇₃ = 0.125

Δφ₇₄= φ₇ – φ₇₄ = -0.275

Δφ₈₁= φ₈ – φ₈₁ = -0.1

Δφ₈₂= φ₈ – φ₈₂ = 0.2

Δφ₈₃= φ₈ – φ₈₃ = 0.1

Δφ₈₄= φ₈ – φ₈₄ = -0.2

Δφ₉₁= φ₉ – φ₉₁ = -0.075

Δφ₉₂= φ₉ – φ₉₂ = 0.125

Δφ₉₃= φ₉ – φ₉₃ = 0.125

Δφ₉₄= φ₉ – φ₉₄ = -0.175

Δφ_10-1= φ₁₀ – φ_10-1 = -0.025

Δφ_10-2= φ₁₀ – φ_10-2 = 0.175

Δφ_10-3= φ₁₀ – φ_10-3 = -0.025

Δφ_10-4= φ₁₀ – φ_10-4 = -0.125

3. 
   Среднеквадратичная погрешность среднего:
   

S_φi =√(∑{Δφ_ik²}/(n{n-1}))

S_φ1= 0.03118

S_φ2= 0.03496

S_φ3= 0,04346

S_φ4= 0,04472

S_φ5= 0,04472

S_φ6i= 0,04472

S_φ7= 0,04048

S_φ8= 0,03333

S_φ9= 0,02739

S_φ10= 0,02297

4. 
   Границы доверительного интервала:
   

Δφ_i=t_α(n)∙ S_φi ; t_α(n)=2.4.

Δφ₁=0,07483

Δφ₂=0,0839

Δφ₃=0,10431

Δφ₄=0,10733

Δφ₅=0,10733

Δφ₆=0,10733

Δφ₇=0,09716

Δφ₈=0,08

Δφ₉=0,06573

Δφ₁₀=0,05514

В среднем: Δφ= 0,088.

5. 
   Логарифм r для каждого значения r: см. 8-й столбец таблицы 1.
   

Графики зависимостей φ(r) и φ(lnr):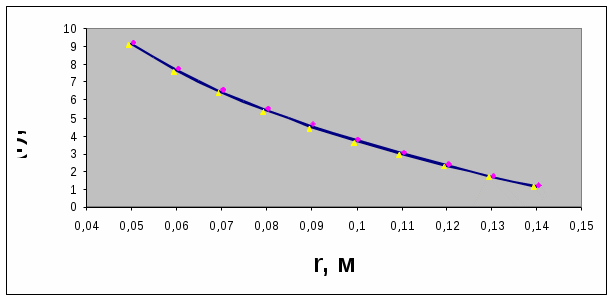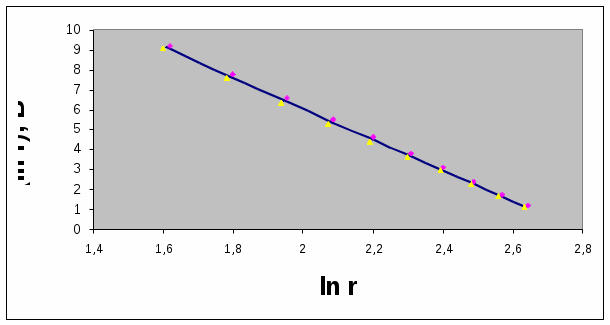





Точки вокруг графиков – координаты случайных погрешностей измерений r и φ.

Δr_i= Δr_i+1=0,5 мм.
Исследование электростатического поля (таблица 2):

№	r =(r +r )/2, м	1/r ,м	Е ,В\м	С ,В
1	0,055	18,18182	147,5	8,1125
2	0,065	15,38462	120	7,8
3	0,075	13,33333	105	7,875
4	0,085	11,76471	90	7,65
5	0,095	10,52632	80	7,6
6	0,105	9,52381	72,5	7,6125
7	0,115	8,695652	67,5	7,7625
8	0,125	8	62,5	7,8125
9	0,135	7,407407	55	7,425

6. 
   Средние значения E_m:
   

E_m=(φ_i- φ_i+1)/(r_i+1-r_i)=U/L

См. 4-й столбец таблицы 2.

7. 
   Относительная погрешность δ_Е:
   

δ_Еm=√{(ΔU/U)²+(ΔL/L)²},

где

U= φ_i- φ_i+1; ΔU=√{(Δφ_i)²+(Δφ_i+1)²};

L= r_i+1-r_i; ΔL=√{(Δr_i)²+(Δr_i+1)²}.

δ_Еm1 =0,103

δ_Еm2 =0,132

δ_Еm3 = 0,159

δ_Еm4 =0,183

δ_Еm5 =0,202

δ_Еm6 =0,212

δ_Еm7 =0,199

δ_Еm8 =0,180

δ_Еm9 =0,171

8. 
   Границы доверительного интервала ΔE_m:
   

ΔE_m=│E_m│∙ δ_E

ΔE_m1= 15,335

ΔE_m2 =15,849

ΔE_m3 =16,707

ΔE_m4 =16,459

ΔE_m5 =16,199

ΔE_m6 =15,358

ΔE_m7 =13,460

ΔE_m8 =11,258

ΔE_m9 = 9,420

В среднем ΔE_m= 14,45.

9. 
   Зависимости E(r) и E(1/r) с указанием погрешностей: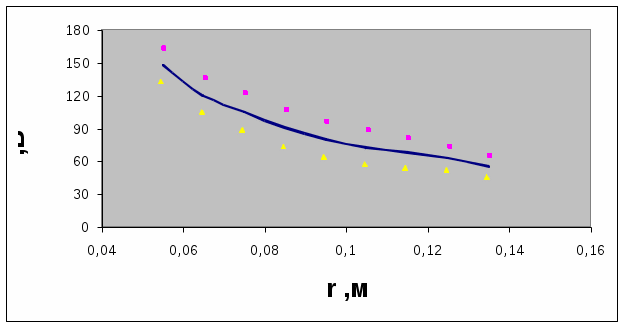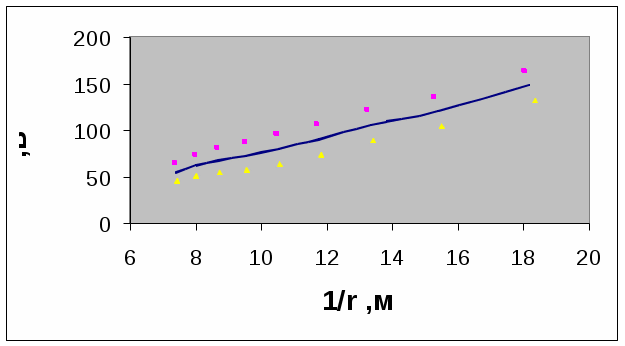
   

10. 
    Константы С_m:
    

С_m=│E_m(r_m)│∙ r_m

См. 5-й столбец таблицы 2.

11. 
    Относительная погрешность δ_­­_Cm:
    

δ_­­_Cm=√{(ΔE_m/E_m)²+(Δr_m/r_m)²}

δ_­­_Cm1 =0,104

δ_­­_Cm2 =0,132

δ_­­_Cm3 =0,159

δ_­­_Cm4 =0,183

δ_­­_Cm5 =0,203

δ_­­_Cm6 =0,212

δ_­­_Cm7 =0,199

δ_­­_Cm8 =0,180

δ_­­_Cm9 =0,171

12. 
    Границы доверительного интервала С_m:
    

ΔС_m=С_m ∙δ_Cm
ΔС_m1 =0,847

ΔС_m2 =1,032

ΔС_m3 =1,254

ΔС_m4 =1,4

ΔС_m5 =1,539

ΔС_m6 =1,613

ΔС_m7 =1,548

ΔС_m8 =1,408

ΔС_m9 =1,272

В среднем ΔС_m=1,324.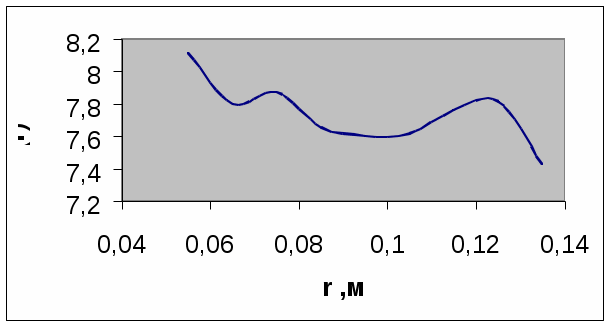




График зависимости C(r) не похож на график постоянной величины; следовательно, велика погрешность расчётов.