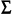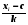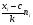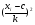математика 4. Работа 2 Случайные величины. 19 вариант. Задача 1
 Скачать 201.17 Kb. Скачать 201.17 Kb.
|
            Работа №2 Случайные величины. 19 - вариант. Задача 2.1. В каждом из n независимых испытаний событие А происходит с постоянной вероятностью 0,36. Вычислить все вероятности рk, k = 0, 1, 2, ..., 11, где k частота события А. Построить график вероятностей рk. Найти наивероятнейшую частоту. Задано: n = 10, p = 0,49, q = 1 - p = 0,51. Найти: р0, р1, р2 , ..., р10 и k. Используя формулу Бернулли. Значение р0 вычисляем по первой из формул, а остальные вероятности рk - по второй. Для формулы вычисляем постоянный множитель р/q = 0,49/ 0,51 = 0,96780, р0 = 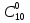 *0,490 * 0,5110 = 0,00119042. *0,490 * 0,5110 = 0,00119042.Результаты вычислений запишем в таблице 1. Если вычисления верны, то должно выполняться равенство 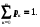 По найденным значениям вероятностей построим их график (рис. 1). Найдем наивероятнейшую частоту по заданным условиям: np - q 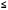 k k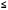 np + p, np + p,np - q = 10 * 0,49 - 0,51 = 4,39. np + p= 10 * 0,49+0,49= 5,39 Значит, наивероятнейшая частота k = 5 и, было получено ранее, значение 5 является максимальным. Таблица 1
0,10 0,5 1,0 1,5 2,0 2,5 3,0 1 2 3 4 5 6 7 8 9 10 Рисунок 1 График вероятностей рk Задача 2.2. В каждом из n независимых испытаний событие А происходит с постоянной вероятностью 0,47. Найти вероятность того, что событие А происходит: а) точно 330 раз; б) меньше чем 330 и больше чем 284 раз; в) больше чем 330 раз. а) Задано: п = 760, р = 0,47, М = 330. Найти: Р760(330). Используем локальную теорему Муавра - Лапласа . Находим: 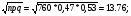 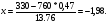 Значение функции (x) найдем из таблицы : (1,98) = 0,0562, P760(330) = 0,0562/ 13,76 = 0,00408. б) Найти: Р760(284 Используем интегральную теорему Муавра - Лапласа . Находим:  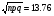 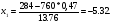 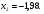 Значение функции Ф(х) найдем из таблицы : Р760(284 Имеем: 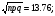 х1 = -1,98, х1 = -1,98, 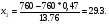 Р760(330 а) точно 2 неправильных соединений; б) меньше чем 3 неправильных соединений; в) больше чем 8 неправильных соединений. а) Задано: n = 5600, p = 1/800, k = 2. Найти: Р800(2). Получаем: = 5600 * 1/800 = 7. Р800(2) = 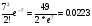 . .б) Задано k<3. Найти: Р200(k<3). Имеем: = 7. Р800(k<3) = Р800(0) + Р800(1) + Р800(2) = 0,0223 + 0,0009 + 0,0064 = 0,0296. в) Задано k > 8. Найти: Р800(k > 8). Находим = 7. Эту задачу можно решить проще, найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Принимая во внимание предыдущий случай, имеем Р800(k>8) = 1 – Р800(k 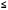 8) = 1 - Р800(k<9) = 1 - 0,7291 = 0,2709. 8) = 1 - Р800(k<9) = 1 - 0,7291 = 0,2709.Задача 2.6. Случайная величина Х задана рядом распределения.
Найти функцию распределения F(x) случайной величины Х и построить ее график. Вычислить для Х ее среднее значение ЕХ, дисперсию DX и моду Мо. R = 4 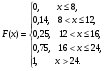 Построим график функции распределения F(x) . Среднее значение ЕХ вычисляем по формуле: ЕХ = 8*0,11 + 12*0,14 + 16*0,5 + 24*0,25 = 16,56. Дисперсия: Е(Х2) = 82*0,11 + 122*0,14 + 162*0,5 + 242*0,25 = 299,2 DX = 299,2 – 16,522 = 26,2896. 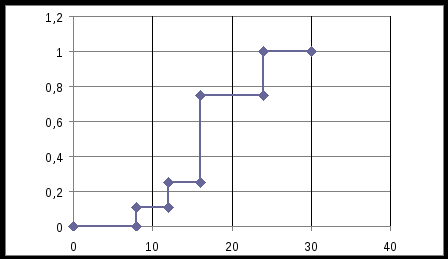 График функции распределения Задача 2.7. Случайная величина Х задана функцией плотности вероятности f(x) = 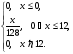 Найти функцию распределения F(x) случайной величины Х. Построить график функции f(x) и F(x). Вычислить для Х ее среднее значение ЕХ, дисперсию DX, моду Мо и медиану Ме. К = 8, R = 12. Функцию распределения F(х) непрерывной случайной величины найдем по формуле: 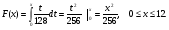 Поэтому 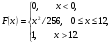 Построить графики функций f(x) и F(x). Среднее значение Х вычисляем по формуле: ЕХ = 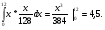 Для нахождения дисперсии Х воспользуемся формулами: Е(Х2) = 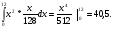 DX = 40,5 – (4,5)2. Из графика видно, что f(x) достигает максимума в точке х = 1/2 и, значит, Мо = 12. Для нахождения медианы Ме нужно решить уравнение х2/ 256 = 1/2, или х2 = 128. Имеем х = 11,31, Ме = 11,31. 6 3 6 12 х График функции плотности вероятности f(x). 6 3 6 12 х График функции распределения F(х). Работа №3. Задача 3.1 По выборкам А и В
среднее арифметическое 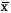 , ,дисперсию 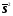 , ,стандартное отклонение 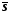 , ,моду Мо, медиану Ме. Задача 3.2. Вычислить несмещенные оценки параметров генеральной совокупности 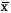 ,S2, S по ,S2, S по выборкам А и В (используя результаты, полученные в задаче 3.1.), а также по первому столбцу выборки В. Выборка А6
N = 73 Начало первого интервала: 0 Длина интервала: 1 Выборка В6
N = 237 Начало первого интервала: 285 Длина интервала: 7 Решение задач. Задача 3.1. Сначала решим задачу по выборке А. Находим: хmin = 0 и хmax = 11. Размах (11 - 0 + 1 = 12) довольно мал, поэтому составим вариационный ряд по значениям (табл. 1). Таблица 1
Все относительные частоты вычисляем с одинаковой точностью. При построении графиков изображаем на оси х значения с 0 по 11 и на оси ni/n - значения с 0 по 0,25 (рис.1 и 2). 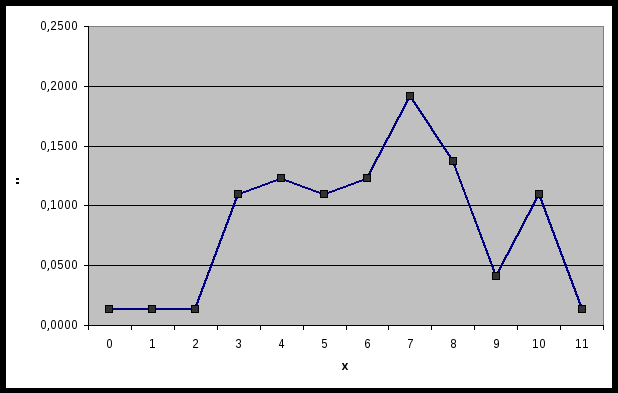 Рис. 1. Полигон вариационного ряда выборки А 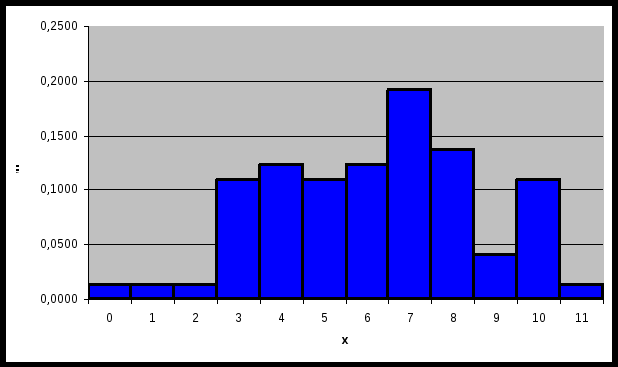 Рис. 2. Гистограмма вариационного ряда выборки А. Эмпирическую функцию распределения F*(x) находим, используя формулу и накопленные частости, из табл. 1. Имеем: 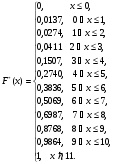 При построении графика F*(x) откладываем значения функции в интервале от 0 до 1,2 (рис. 3). Рис.3. График эмпирической функции распределения выборки А. Вычисление сумм для среднего арифметического и дисперсии по формулам и по вариационному ряду (см. табл. 1) оформляем в табл. 2. По максимальной частоте определяем с = 7, а шаг таблицы k = 1. Далее по формуле вычисляем среднее арифметическое 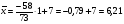 и дисперсию и дисперсию 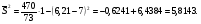 Таблица 2
Стандартное отклонение 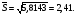 Модой Мо является значение с максимальной частотой, т.е. Мо = 7. Медианой Ме служит 37-е значение вариационного ряда: Ме = 7. Модой Мо является значение с максимальной частотой, т.е. Мо = 7. Медианой Ме служит 37-е значение вариационного ряда: Ме = 7.Теперь по выборке В найдем хmin = 288 и хmax = 350. Размах (350 - 288 + 1 = 63) достаточно большой, поэтому составим вариационный ряд по интервалам значений, используя при выборке заданные начало первого интервала и длину интервала (табл.3). Таблица 3
Рис. 4. Полигон вариационного ряда выборки В. Рис. 5. Гистограмма вариационного ряда выборки В. При построении графиков откладываем по оси х значения с 285 по 355 и по оси ni/n - значения с 0 по 0,3(рис. 4 и 5). Далее учитываем, что в качестве представителя каждого интервала взят его конец. Принимая за координаты точек концы интервалов и соответствующие накопленные частости (см. табл. 3) и соединяя эти точки прямыми, построим график эмпирической функции распределения (рис. 6). Рис. 6. График эмпирической функции распределения выборки В. Для вычисления среднего арифметического и дисперсии по формулам и по табл. 3 определим с = 316 и k = 7. Суммы вычислим с помощью табл. 4 (табл. 4). По формулам вычисляем среднее арифметическое 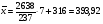 и дисперсию и дисперсию 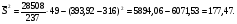 Стандартное отклонение 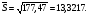 Моду находим по формуле: Моду находим по формуле:Мо = 313 + 7 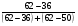 = 317,8. = 317,8.Таблица 4
Медиану находим по формуле: Ме =. Задача 3.2. По формуле находим несмещенные оценки дисперсии и стандартного отклонения: n = 73, S-2 = 5,8143, S2 = 73/72 5,8143 = 5,8951, S = 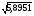 = 2,43. = 2,43.Для выборки В имеем 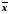 = 393,92, = 393,92, 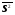 = 177,47, n = 237, S2 = 237/236 177,47 = 178,222, S = 13,35. = 177,47, n = 237, S2 = 237/236 177,47 = 178,222, S = 13,35.Несмещенные оценки для первого столбца выборки В получаются аналогично (если эта выборка содержит мало повторяющихся элементов, вариационный ряд можно не составлять). |