LAB36 Антон. Лабораторная работа 36 эффективное кодирование на примере кода хаффмана выполнил студент группы рт0701 Ольхин Антон Владимирович
 Скачать 169.5 Kb. Скачать 169.5 Kb.
|
|
Кафедра передачи дискретных сообщений и телеграфии Лабораторная работа №36 ЭФФЕКТИВНОЕ КОДИРОВАНИЕ НА ПРИМЕРЕ КОДА ХАФФМАНА Выполнил студент группы РТ0701 Ольхин Антон Владимирович Москва 2011 Цель работы: Изучение принципов эффективного кодирования источников дискретных сообщений. Схема лабораторного макета. 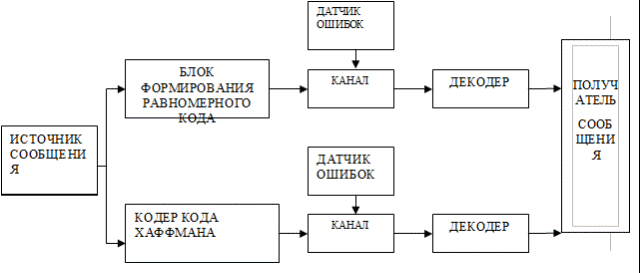 Индивидуальное задание.Изучить принцип эффективного кодирования алфавита источника дискретных сообщений (ИДС) по методу Хаффмана. Сформировать кодовые комбинации для передачи заданной последовательности знаков алфавита при кодировании алфавита ИДС равномерным кодом; при кодировании алфавита ИДС кодом Хаффмана. Определить значения Нmax , Нреал и nсред для анализируемого варианта. Оценить значение Коэ и Ксж. p(z1)=0.18 p(z2)=0.14 p(z3)=0.03 p(z4)=0.24 p(z5)=0.05 p(z6)=0.36 Закодируем этот алфавит равномерным кодом. N=6 , нам потребуются 3-х разрядные кодовые комбинации. Допустим: z1->001 z2->010 z3->011 z4->100 z5->101 z6->110 Слово алфавита z1z2z3z4z5z6 будет кодировано следующим образом: 001010011100101110 Найдем значение энтропии.  Найдем значение максимальной энтропии (при вероятности появления символа 1/N)  Избыточность источника равна: Найдем кодовые комбинации для того же алфавита по методу Хаффмана. Построим таблицу перехода вероятностей. Д 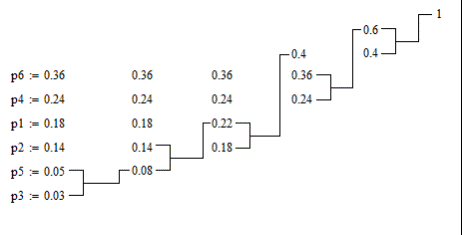 алее построим дерево кодовых слов. 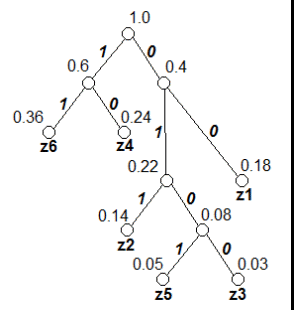 В соответствии с ним находим кодовые комбинации для каждого символа алфавита. z1->00 n1=2 z2->011 n2=3 z3->0100 n3=4 z4->10 n4=2 z5->0101 n5=4 z6->11 n6=2 Выбранный код обладает свойством префиксности. Комбинация z1z2z3z4z5z6 кодируется: 00011010010010111 Найдем среднее число двоичных символов на знак алфавита.  Очевидно, неравномерный код Хаффмана более компактен, чем равномерный код. Найдем коэффициенты относительной эффективности и сжатия. Пункт 1.2 Наблюдение и анализ статистики сообщения и процесса кодирования и декодирования (приотсутствии ошибок).  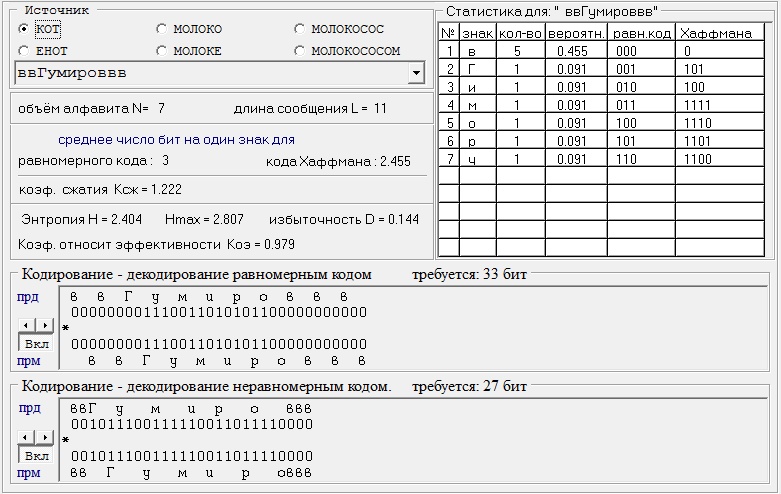  Код Хаффмана: Таблица переходных вероятностей 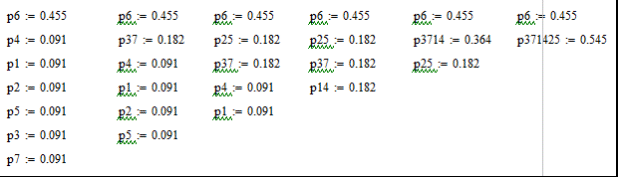 Дерево кодовых слов. 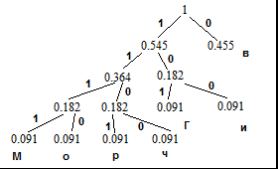  П 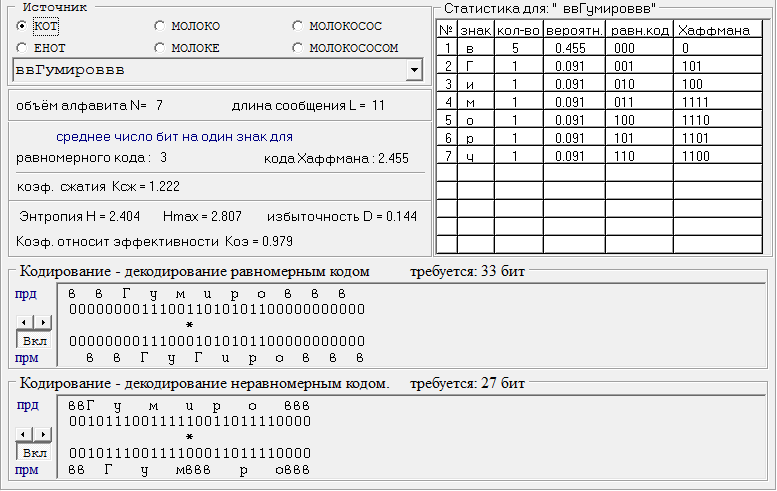 ункт 1.3 Наблюдение и анализ процесса декодирования при наличии ошибок. Вывод: Исходя из результатов лабораторной работы, можно сделать вывод, что неравномерный код Хаффмана более компактный, но равномерный код более устойчив к помехам. Контрольные вопросы: 2) Принцип построение кодовой комбинации при кодировании неравномерным кодом. Построение кода Хаффмана начинается с упорядочивания указанных знаков по убыванию значений Рi. Затем по результатам таблицы строится кодовое дерево. 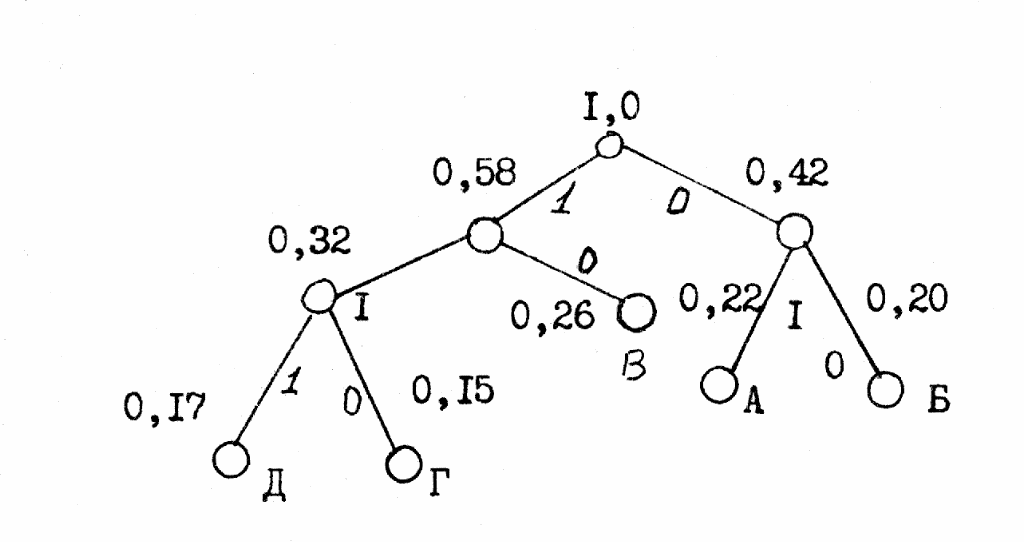 Из точки Рi=1,0 направляем две ветви, и той, у которой в соответствии с колонкой 5 таблицы 1 вероятность больше (Рi =0,58), присваиваем символ 1, другой — 0. Код висячей вершины и будет кодом при последовательном прохождении от начала дерева к ней. 4) Показатели количественной оценки эффективности неравномерного кодирования, Эффективность неравномерных кодов оценивается коэффициентом относительной эффективности который показывает степень использования статистической избыточности. Для оптимальных кодов Коэ=1. Отношение среднего числа двоичных символов, приходящихся на один знак алфавита, при кодировании заданного источника неравномерным кодом к длине кодовой комбинации в случае кодирования источника равномерным кодом называется коэффициентом сжатия Ксж. 6) Принцип декодирования последовательности префиксного кода. При декодировании последовательности комбинаций префиксного кода определение кода каждого знака производится однозначно. В противном случае, т.е. для комбинаций непрефиксного кода характерна неоднозначность декодирования. Пусть, например, некоторый код удовлетворяет требованию префиксности, т.е. знакам алфавита соответствуют кодовые комбинации вида: А-00 Б-01 B-101 Г-100. Составим произвольно комбинацию передаваемых знаков алфавита и соответствующую ей кодовую последовательность: БАБВГВГЕГААБ. 01000110110010101100000001.() Эта последовательность декодируется однозначно: 01 00 01 101 100 101 01 100 00 00 01 Б А Б В Г В Б Г А А Б Рассмотрим другой случай, когда кодирование ансамбля знаков проведено по кодовой таблице вида А-00; Б-01; В-001; Г-010. Тогда последовательность кодовых комбинаций того же сообщения будет иметь вид 01000100101000101010000001. В этом случае возможны различные варианты декодирования: 01 00 01 001 01 00 01 01 010 00 00 01 Б А Б В Б А Б Б Г А А Б или 010 001 001 010 001 01 010 00 00 01 Г В В Г В Б Г А А Б |
