Лаба По Физике. Лаба №36. Лабораторная работа 36 I. Название работы
 Скачать 163.5 Kb. Скачать 163.5 Kb.
|
|
Дата Фамилия Группа Лабораторная работа №36 I.Название работы: Измерение магнитного момента полосового постоянного магнита при использовании компаса, линейки и секундомера. Цель работы: Измерение магнитного момента полосового постоянного магнита II.Краткое теоретическое обоснование: П одвесим полосовой постоянный магнит на очень тонкой нити в некотором магнитном поле. Поле создается каким – либо устройством или Землей, (в лабораторной установке используется магнитное поле Земли с индукцией B0). Направление вектора индукции магнитного поля B0 определяем по компасу. Числовое значение его модуля нам может быть неизвестным. Ориентируем полосовой магнит вектора индукции магнитного поля B0 (в условиях эксперимента ориентируем его северным концом к N). Дождемся, пока магнит перестанет колебаться. Затем осторожно отклоним его на малый угол γ, не более нескольких градусов. На магнит станет действовать возвращающий момент M. где pm – магнитный момент полосового магнита. При малых углах γ sin γ = γ. Поэтому из (6.1) получим: Запишем основное уравнение динамики вращательного движения где ε – угловое ускорение магнита. I – момент инерции магнита относительно центра масс где m – масса магнита (определяется взвешиванием), a – длина магнита, b – ширина магнита (определяется измерениями) Из уравнений (6.2) и (6.3) получим 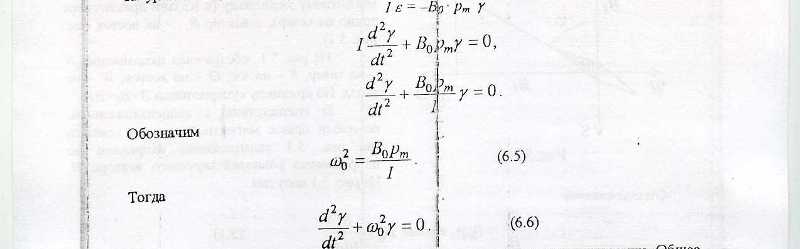 Получено линейное однородное дифференциальное уравнение второго порядка. Общее решение уравнения имеет вид γ = Acos (ωt + α) Следовательно, движение магнита представляет собой гармоническое колебание с периодом 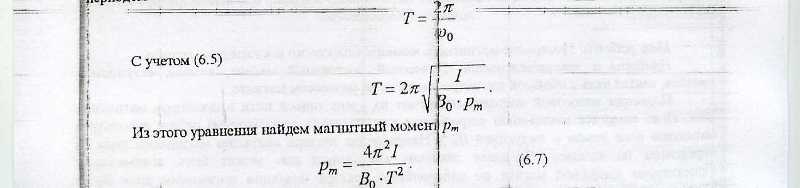 Момент инерции I определяется по уравнению (6.4), период колебаний магнита можно получить экспериментально. Числовое значение индукции B0 нам неизвестно. Поэтому, для определения магнитного момента pm нужно еще одно уравнение. Найдем его. Если дополнительное магнитное поле с индукцией B1 создать полосовым магнитом с магнитным моментом pm. где x – расстояние от центра полосового магнита до оси стрелки компаса. Подставив это выражение в уравнение (6.8), получим Из этого уравнения следует, что Подставив уравнение (6.9) в уравнение (6.7), получим искомый магнитный момент pm. Из уравнения (6.10) следует, что для определения магнитного момента pm полосового постоянного магнита необходимо вычислить по уравнению (6.4) момент инерции I магнита, период T качания магнита в магнитном поле Земли, угол φ отклонения стрелки компаса от магнитного меридиана. III.Рабочие формулы и единицы измерения.  IV.Измерительные приборы и принадлежности. Полосовой постоянный магнит Компас Секундомер Линейка Тонкая нить с обоймой для закрепления ее на полосовом магните V.Результаты измерения.
VI. Черновые записи и вычисления. Tср = (4,1 + 4,13 + 4,25 + 4,25 + 4,37) / 5 = 4,234 [c] T = 41 / 10 = 4,1 [c] ΔТi = | 4,234 − 4,1 | = 0,134 [c] T = 62 / 15 = 4,13 [c] ΔТi = | 4,234 − 4,13 | = 0,101 [c] T = 85 / 20 = 4,25 [c] ΔТi = | 4,234 − 4,25 | = 0,016 [c] T = 108 / 25 = 4,32 [c] ΔТi = | 4,234 − 4,32 | = 0,086 [c] T = 131 / 30 = 4,37 [c] ΔТi = | 4,234 − 4,37 | = 0,133 [c] ΔТср = 0,134 / 5 = 0,0268 [c] δТср = ( 0,0268 / 4,234 ) • 100 % = 0,63297 ΔТср = 0,101 / 5 = 0,0201 [c] δТср = ( 0,0201 / 4,234 ) • 100 % = 0,47552 ΔТср = 0,016 / 5 = 0,0032 [c] δТср = ( 0,0032 / 4,234 ) • 100 % = 0,07558 ΔТср = 0,086 / 5 = 0,0172 [c] δТср = ( 0,0172 / 4,234 ) • 100 % = 0,40642 ΔТср = 0,133 / 5 = 0,0265 [c] δТср = ( 0,0265 / 4,234 ) • 100 % = 0,62667 φср = ( 2 + 3 + 3 + 2 + 3 + 2 ) = 2,5 [град] Δφ ср = ( 0,5 • 6 ) / 6 = 0,5 [град] δφср = ( 0,5 / 2,5 ) • 100% = 20 [%] Δφ = | 2 − 2,5 | = 0,5 [град] δφср = ( 0,5 / 2,5 ) • 100% = 20 [%] Δφ = | 3 − 2,5 | = 0,5 [град] δφср = ( 0,5 / 2,5 ) • 100% = 20 [%] Δφ = | 3 − 2,5 | = 0,5 [град] δφср = ( 0,5 / 2,5 ) • 100% = 20 [%] Δφ = | 2 − 2,5 | = 0,5 [град] δφср = ( 0,5 / 2,5 ) • 100% = 20 [%] Δφ = | 3 − 2,5 | = 0,5 [град] δφср = ( 0,5 / 2,5 ) • 100% = 20 [%] Δφ = | 2 − 2,5 | = 0,5 [град] VII. Основные выводы. Мы измерили магнитный момент полосового постоянного магнита |
