анализ коррект. Лабораторная работа 4. использование Корреляционного анализа в задачах статистического исследования результатов научного эксперимента

• Название: Лабораторная работа 4. использование Корреляционного анализа в задачах статистического исследования результатов научного эксперимента
• Анкор: анализ коррект
• Дата: 20.04.2022
• Размер: 335.5 Kb.
• Имя файла: Korr_analiz.doc
• Тип: Лабораторная работа; #486727

Лабораторная работа №4. использование Корреляционного анализа в задачах статистического исследования результатов научного эксперимента
Цель работы: Приобретение навыков корреляционного анализа в задачах статистического исследования с применением программного продукта MSExcel.
Теоретический материал и инструкции по применению программного средства
Параметрический корреляционный анализ
Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками. Обычно связь между выборками носит не функциональный, а вероятностный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей разли­чают корреляцию и регрессию.

Корреляционный анализ состоит в определении степени связи между двумя случайными величинами Xи Y. В качестве меры такой связи используется коэффи­циент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (x_i, y_i) из совместной генеральной совокупности Xи Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от измерения (способа шкалирования) величин Xи Y.

Для оценки степени взаимосвязи величин Xи Y, измеренных в количественных шкалах, используется коэффициент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки Xи Y распределены по нормальному закону. При таком распределении большая часть значений группируется около некоторого среднего значения, по обе стороны от которого частота наблюдений равномерно снижается.

1. Линейный коэффициент корреляции — параметр, который характеризует степень линейной взаимосвязи между двумя выборками, рассчитывается по формуле 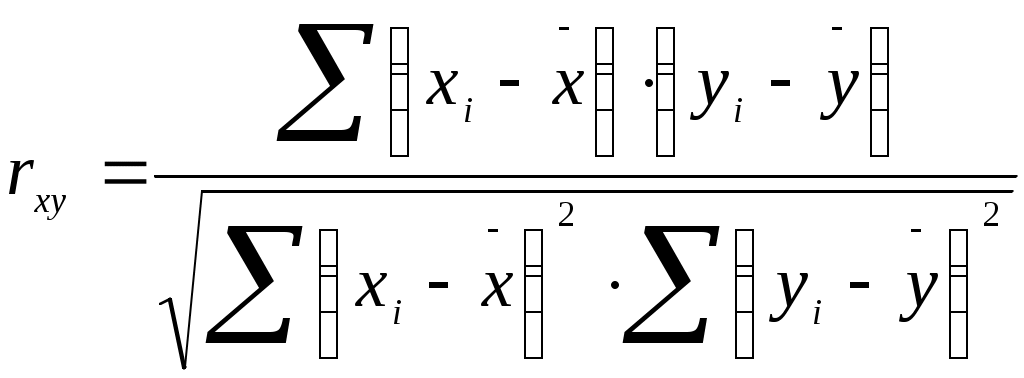(4.1):

(4.1)

где х_i — значения, принимаемые в выборке X,

y_i — значения, принимаемые в выборке Y;

— средняя по X, — средняя по Y.

Коэффициент корреляции изменяется от -1 до 1. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно, произошла ошибка в вычислениях. При значении 0 линейной зависимости между двумя выборками нет.

Знак коэффициента корреляции очень важен для интерпре­тации полученной связи. Если знак коэффициента линейной корреляции — плюс, то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости.

Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости. (см. таблицу 4.1):

Таблица 4.1 Теснота связи и величина коэффициента корреляции.

Коэффициент корреляции rxy	Теснота связи
+ 0,91-1,0	Очень сильная
+ 0,81-0,9	Весьма сильная
+ 0,65-0,8	Сильная
+ 0,45-0,64	Умеренная
+ 0,25-0,44	Слабая
До + 0,25	Очень слабая
«+» - прямая зависимость «-» - обратная зависимость

Для того чтобы оценить наличие связи между двумя переменными, также можно использовать t-статистику Стьюдента, которая оценивает отношение величины линейного коэффициента корреляции к среднему квадратичному отклонению и рассчитывается по формуле 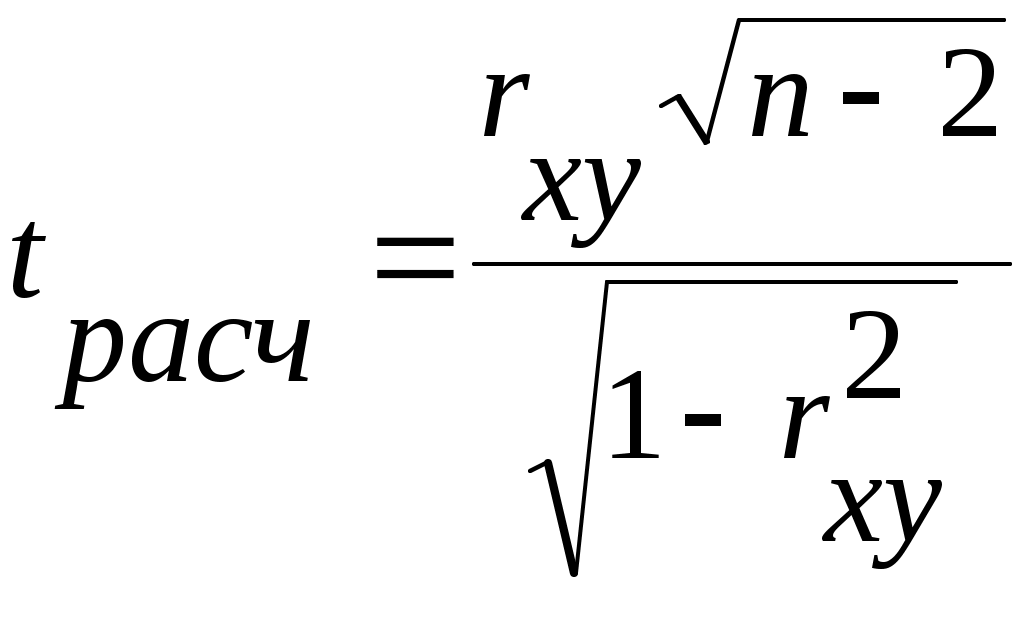(4.2)

(4.2)

Полученную величину t_расч сравнивают с табличным значением t-критерия Стьюдента с n-2 степенями свободы. Если t_расч > t_табл, то практически невероятно, что найденное значение обусловлено только случайными совпадениями величин X и Y в выборке из генеральной совокупности, т.е. существует зависимость между X и Y. И наоборот, если t_расч < t_табл, то величины X и Y независимы.

Проведение параметрического корреляционного анализа

Условие задачи: По 20 заводам производителям нефтеперекачивающих насосов были установлены затраты на рекламную кампанию и количество проданных насосов, после ее проведения каждым заводом. Необходимо определить коэффициент корреляции между исследуемыми признаками, используя:

1. 
   Формулу линейного коэффициента корреляции.
   
2. 
   Статистическую функцию КОРРЕЛ.
   

Расчет коэффициента корреляции Пирсона с использованием формулы (4.1).

Откройте новую книгу MS Excel и создайте таблицу согласно рис. 4.1, сохраните в своей папке под именем Параметрический_Анализ.xls.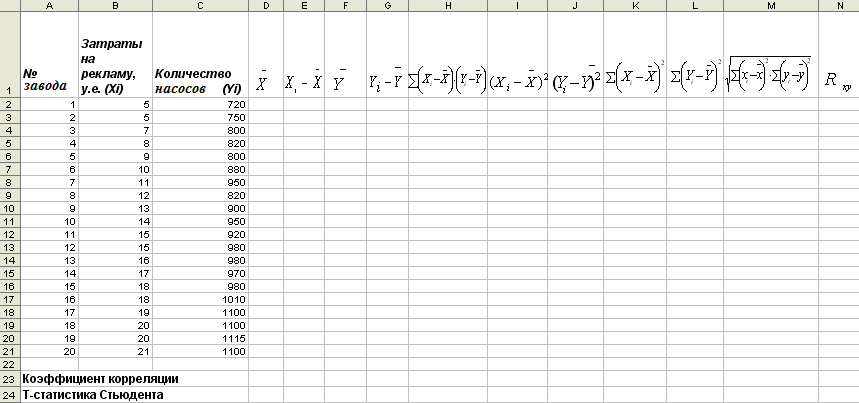



Рис.4.1 - Данные для задачи.

1. 
   В ячейке D2 рассчитайте (среднее значение переменной ).
   
2. 
   В диапазоне ячеек E2:E21 рассчитайте (отклонение значений переменной от среднего значения ).
   
3. 
   В ячейке F2 рассчитайте (среднее значение переменной ).
   
4. 
   В диапазоне ячеек G2:G21 рассчитайте (отклонение значений переменной от среднего значения ).
   
5. 
   В ячейке H2 рассчитайте сумму произведений , воспользовавшись математической функцией СУММПРОИЗВ.
   
6. 
   В диапазоне ячеек I2:I21 рассчитайте (квадраты отклонений значений переменной от среднего значения ).
   
7. 
   В диапазоне ячеек J2:J21 рассчитайте (квадраты отклонений значений переменной от среднего значения ).
   
8. 
   В ячейке K2 рассчитайте .
   
9. 
   В ячейке L2 рассчитайте .
   
10. 
    В ячейке M2 рассчитайте .
    
11. 
    В ячейке N2 рассчитайте коэффициент линейной корреляции .
    
12. 
    Сделайте вывод о тесноте связи между затратами на рекламу и количеством привлеченных туристов и направлении этой связи.
    

Расчет коэффициента корреляции с использованием функции КОРРЕЛ.

1. 
   В ячейке D23 рассчитайте коэффициент корреляции, используя функцию КОРРЕЛ из категории Статистические.
   

Синтаксис функции КОРРЕЛ:

КОРРЕЛ (массив 1; массив 2):

где массив 1 – ссылка на диапазон ячеек первой выборки (X);

массив 2 – ссылка на диапазон ячеек второй выборки (Y).

2. 
   Оцените значимость коэффициента корреляции. С этой целью рассматриваются две гипотезы. Основная Н₀: _xy=0 и альтернативная Н₁: _xy≠0. Для проверки гипотезы Н₀ рассчитайте t-статистику Стьюдента по формуле (4.2) в ячейке D24. В нашем случае число степеней свободы ν = n-2=20-2 = 18 (количество наблюдений минус два).
   
3. 
   Сравните полученное значение с критическим значением t_ν,α распределения Стьюдента. (При ν =18 и вероятности α = 0,05, t_{ν,α,табл} = 1,734). Сделайте вывод о значимости коэффициента корреляции.
   

Расчет коэффициента корреляции с использованием Пакета анализа MS Excel.

1. 
   (Для версии XP) Сначала убедитесь, что был активизирован Пакет анализа, т.е. в меню Сервис есть команда Анализ данных. Если нет, то выполните команду Сервис/Надстройки. В диалоговом окне Надстройки установите флажок Пакет анализа и щелкните по кнопке ОК.
   
2. 
   (Для версии 2007 и выше) Сначала убедитесь, что был активизирован Пакет анализа, т.е. в меню Данные есть команда Анализ данных. Если нет, то выполните команду Сервис/Надстройки. В диалоговом окне Надстройки установите флажок Пакет анализа и щелкните по кнопке ОК.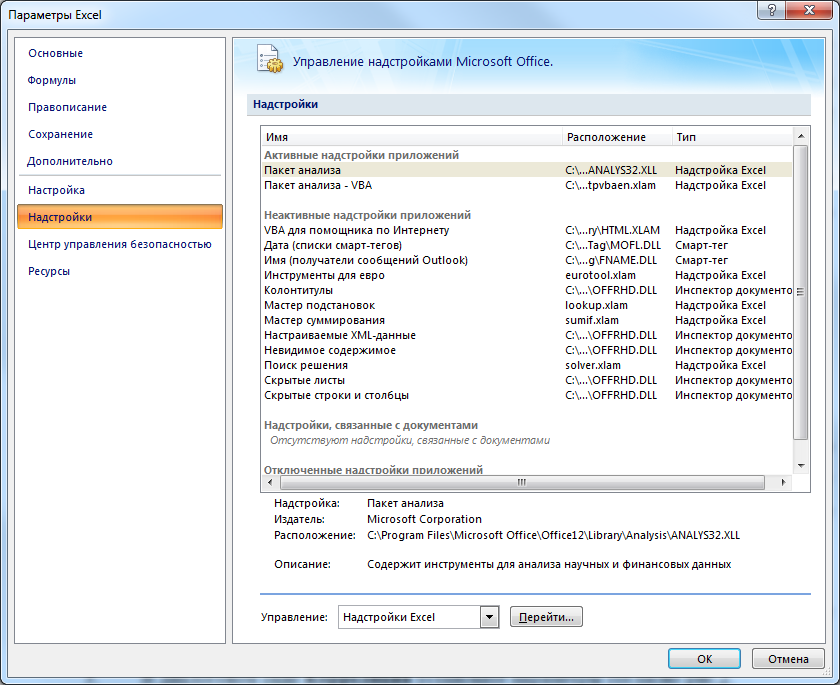
   

3. 
   Далее выполните команду Анализ данных. Выберите инструмент анализа Корреляции.
   
4. 
   В диалоговом окне Корреляция установите параметры согласно рис.4.2.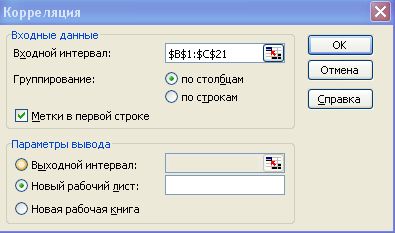
   

Рис.4.2 - Окно Корреляция.

5. 
   На новом рабочем листе получите значение коэффициента корреляции. Сравните с ранее полученными результатами.
   
6. 
   Сохраните изменения в книге.
   
7. 
   Далее выберите инструмент Описательная статистика и проанализируйте данные с установленными параметрами согласно рис. 4.3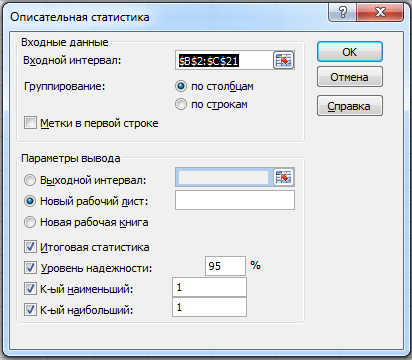
   

Рис.4.3 - Описательная Статистика.
ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ

1. 
   Получить у преподавателя два номера заданий.
   
2. 
   Используя программный продукт MS Excel и рассмотренный пример необходимо определить коэффициент корреляции между исследуемыми признаками, используя:
   

• 
  Формулу линейного коэффициента корреляции.
  
• 
  Статистическую функцию КОРРЕЛ.
  

3. 
   Продемонстрировать преподавателю электронный вариант решения поставленной задачи.
   

СОДЕРЖАНИЕ ОТЧЕТА

1. 
   Титульный лист.
   
2. 
   Тема, цель и основное содержание работы.
   
3. 
   Описание процесса решения задачи.
   
4. 
   Промежуточные и итоговые результаты.
   
5. 
   Выводы по работе.
   

ВАРИАНТЫ ЗАДАНИЙ

Номер завода	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	№ варианта
Затраты у.е.	1	1	2	3	3	3	4	5	6	7	8	10	12	12	12	15	15	16	18	19	1
Затраты у.е.	1	1	1	2	3	3	4	5	6	8	8	10	11	12	12	15	16	16	17	19	2
Затраты у.е.	1	2	2	3	5	4	4	6	7	7	8	9	10	10	10	11	15	17	18	20	3
Затраты у.е.	1	2	3	3	4	4	4	6	6	9	9	10	12	11	15	15	15	16	17	19	4
Затраты у.е.	1	2	2	3	3	3	4	6	6	7	8	10	12	13	14	15	15	16	18	19	5
Затраты у.е.	1	1	2	3	4	4	4	6	6	7	8	10	12	12	13	15	15	16	17	20	6
Затраты у.е.	1	1	2	2	2	2	4	6	6	7	8	10	12	12	12	15	15	16	18	19	7
Затраты у.е.	1	1	2	3	3	3	4	7	7	7	8	10	12	12	12	15	15	16	18	19	8
Затраты у.е.	1	2	3	4	4	4	4	6	6	7	8	10	12	12	14	15	15	16	18	21	9
Затраты у.е.	1	2	2	3	3	3	4	6	6	7	8	10	12	13	14	15	15	16	18	22	10
Затраты у.е.	2	2	3	3	5	3	4	6	6	7	8	10	12	12	12	15	15	16	18	19	11
Затраты у.е.	1	1	2	3	3	4	5	6	6	7	8	10	12	12	12	14	15	16	18	19	12
Затраты у.е.	1	1	2	3	3	5	5	6	6	7	8	10	11	12	12	15	15	16	18	19	13
Затраты у.е.	1	1	2	2	4	3	4	5	6	7	8	10	12	12	10	15	15	16	18	18	14
Затраты у.е.	1	1	2	3	3	3	4	6	6	7	8	10	11	12	14	15	16	16	18	18	15
Затраты у.е.	2	1	2	3	3	3	4	6	7	7	9	9	12	12	12	15	15	16	17	19	16
Затраты у.е.	1	1	2	3	3	3	4	6	6	7	8	9	9	9	12	15	15	16	18	19	17
Затраты у.е.	1	1	2	3	3	3	4	6	6	7	8	8	12	13	12	15	15	16	18	19	18
Затраты у.е.	1	1	2	3	3	3	4	6	6	6	8	11	12	12	14	15	15	16	18	19	19
Затраты у.е.	3	1	2	3	3	3	5	6	6	7	8	10	12	13	12	15	15	19	19	19	20

ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ:

1. 
   В чем заключается суть корреляционного анализа?
   
2. 
   Что называется линейным коэффициентом корреляции?
   
3. 
   Какими функциями реализован корреляционный анализ в MSExcel?