Лабораторная работа 4 Изучение изотермического процесса. Цель работы

• Название: Лабораторная работа 4 Изучение изотермического процесса. Цель работы
• Дата: 08.02.2021
• Размер: 145.46 Kb.
• Имя файла: mf-01-1.docx
• Тип: Лабораторная работа; #174891

ЛАБОРАТОРНАЯ РАБОТА № 4
Изучение изотермического процесса.
Цель работы: изучить параметры изотермического процесса, экспериментально проверить справедливость закона Бойля-Мариотта.
1.1. Теоретическое введение.

Системы, состоящие из большого числа тел (молекул), называются мак- росистемами. К таким системам относятся, например, газы, жидкости, твердые тела. Системы, между которыми возможен обмен энергией, без учета микро- скопического строения тел, составляющих систему, называется термодинами- ческой системой. Простейшим примером термодинамической системы является идеальный газ.

Идеальным называется газ, молекулы которого приняты за материальные точки и находятся в постоянном хаотическом движении. Между молекулами идеального газа отсутствуют силы притяжения, а отталкивание при соударени- ях происходит по закону упругого удара.

Состояние термодинамической системы однозначно описывается конеч- ным числом параметров, которые называются термодинамическими парамет- рами. Термодинамические параметры (параметры состояния) – физические величины, характеризующие состояние термодинамической системы, например, температура T, давление P, объём V , масса газа m (количество вещества или

число молей

ν  ^m , где μ – молярная масса).

μ

Равновесным состоянием системы называют такое состояние, при кото- ром все ее термодинамические параметры сколь угодно долго остаются неиз- менными в отсутствие внешнего воздействия, при этом давление и температура имеют одинаковые значения во всех частях объема. Всякое изменение состоя- ния системы, характеризующееся изменением ее термодинамических парамет- ров, называется термодинамическим процессом. Термодинамический процесс называется равновесным, если при его протекании система проходит непре- рывный ряд бесконечно близких равновесных состояний. Очевидно, что реаль- ный процесс изменения состояния системы всегда протекает с конечной скоро- стью и поэтому не является равновесным. Однако реальный процесс будет тем ближе к равновесному, чем медленней он протекает. Поэтому равновесные процессы называют квазистатическими. Квазистатический (квазиравновесный) процесс – бесконечно медленный переход термодинамической системы из од- ного равновесного состояния в другое, при котором термодинамическое состо- яние в любой момент времени бесконечно мало отличается от равновесного, и его можно рассматривать как состояние термодинамического равновесия. Тер- модинамический процесс, при протекании которого один из термодинамиче- ских параметров остаётся постоянным, называется изопроцессом (при посто-

янной массе m  const )

В термодинамике часто встречаются квазистатические изопроцессы: изо- хорный – процесс, происходящий при постоянном объеме ( m  const , V=const); изобарный процесс – процесс, в котором давление остается постоянным ( m  const , P=const); изотермический процесс – процесс, происходящий при постоянной температуре ( m  const , T=const) и т.д. Все квазистатические про- цессы можно изобразить в виде графика. Соответствующие кривые называются изохорой (V=const), изобарой (P=const) и изотермой (T=const) и т.д.

Уравнение, выражающее связь между термодинамическими параметрами макросистемы, называется уравнением состояния. Уравнение состояния в об-

щем виде для термодинамической системы может быть записано:

f(P,V,T)  0 .

Конкретный вид функции f предполагается известным из эксперимента. Изу- чая свойства идеального газа, установили ряд законов, определяющих связь термодинамических параметров идеального газа.

Уравнение Клапейрона–Менделеева – уравнение состояния идеального

газа массы m:

PV  ^m RT  vRT , где v  ^m 

количество вещества (количество

μ μ

молей вещества), μ – молярная масса газа (масса 1 моля газа), R- универсаль- ная газовая постоянная.

Для одного моля идеального газа, взятого при нормальных условиях:


0

0
P  1,01310⁵ Па, T  273,15K , V₀=0,0224 м³/моль, (согласно закону Авогадро объ-

ём одного моля равен V₀=22,4 л) по уравнению Клапейрона-Менделеева можно

определить универсальную газовую постоянную

^P0^Vмоля T₀

 const  R

( R  8,31

Дж _).

моль  К

Из уравнения состояния легко получить уравнения изопроцессов, происхо- дящих в идеальном газе, например изохорного, изобарного и изотермического.

Название изопро- цесса	Характеристики изопроцесса	Уравнение изопро- цесса	График
Изотерми- ческий	m  const, T  const. коэффициент все- стороннего сжатия χ   1  V V  P  T	Закон Бойля – Мари- отта: PV  const или P  const V Для данной массы га- за при постоянной температуре (Т = const) произведение давления на объем – величина постоянная.	T1< T2 <T3 P 0 V График процесса – изотерма

Изобари- ческий	m  const, P  const коэффициент объ- емного расшире- ния идеального газа: α  1  dV р V  dТ 0   р	Закон Гей-Люссака: V  V0 (1+ αp t) или V= const T Для данной массы га- за при постоянном давлении P=const объем газа изменяет- ся линейно с темпе- ратурой	V P1> P2 P2 P1 0 T График процесса - изобара
Изохори- ческий	m  const, V  const термический ко- эффициент дав- ления α  1  dP V P  dT 0  V	Закон Шарля: P P0 (1+αVt) P  const T Давление данной массы газа при по- стоянном объёме ме- няется линейно с температурой.	P V1> V2 V2 V1 0 T График процесса - изохора

Связь коэффициентов теплового расширения, термического коэффи- циента давления и коэффициента всестороннего сжатия

Если величинами, определяющими состояние газа, являются: давление P, температура газа T, объём газа V, то их называют макропараметрами состояния. Уравнение, связывающее все три величины для данной массы газа, называется

уравнением состояния и может быть записано в общем виде так: f(P,V,T)=0.

Это означает, что состояние идеального газа определяется только двумя пара- метрами (например, давлением и объёмом, давлением и температурой или объ- ёмом и температурой), третий параметр однозначно определяется двумя други- ми. Следовательно, параметры состояния не являются независимыми. Каждый из этих параметров является функцией двух других. Если термодинамическая система характеризуется параметрами: давление P, температура газа T, объём газа V, то объём V по уравнению состояния можно представить в виде функции остальных двух переменных P и T, т.е. V  V(P,T) .

При термодинамическом равновесии изменения параметров системы свя- заны определенным соотношением. Если T=const , а давление изменяется на бесконечно малую величину dP, то объём получит также бесконечно малое

приращение, определяемое выражением: dV

_ V_



 _P 

dP . Знак T у производной

означает, что T=const.

 _T

Производные, получаемые дифференцированием какой-либо функции двух (или нескольких) аргументов по одному из них в предположении, что все остальные аргументы остаются постоянными, называются частными производ- ными.

Если объём газа изменяется при изменении температуры при P=const.

Тогда бесконечно малое приращение dV при изменении температуры dTвыра-

зится формулой: dV

_ V_



 _T

dT .

 _P

Если изменяется и давление и температура, то приращение объёма равно

сумме: dV

_ V _



 _P

dP+^{ V}


 
T

dT .

 _T  _P

Так как давление и температура связаны уравнением состояния идеально- го газа, то dP и dT не являются независимыми.

При изохорическом процессе dV=0, тогда можно записать:

0 
_ V_

 _P

dP+^{ V}


 
T

dT . Решим это уравнение относительно ^{ dP }


 
dT

_ P _



 _T ^.

 _T

 _P

 _V  _V

Тогда

_ P_

 _T

_ V_


 
 _T

_ V_


/
 _P 

или, учитывая, что

_ V_

 _P

 1/^{ P}


 
V

получим

 _V

 _P  _T

 _T

 _T

_ P_

 _T

_ P _


 
 _V 

_ V_

 _T

или ^{ P }


 
V

_ V_

 _T

_ T_

 _P

 1.

 _V

 _T _P

 _T

_P _V

Полученные формулы позволяют установить связь между коэффициен- том теплового расширения α_P, термическим коэффициентом давления α_Vи мо- дулем всестороннего сжатия (изотермический коэффициент сжимаемости) χ.

₀  _V

P_{0 } dT _V

Изотермический модуль всестороннего сжатия χ определяет отно- сительное изменение объема, вызванного изменением давления на единицу при

постоянной температуре:

_{χ  } 1 _ V _


 
V P

, где dV – изменение объема газа, вы-

 _T

зывающее изменение давления на величину dP; V – первоначальный объем (от- носительным изменением какой-либо величины называется отношение измене- ния этой величины к ее первоначальному значению). Индекс Т у производной показывает, что она берется при Т =const.

Ввиду тождества

_ P_

 _V

_ V_

 _T

_ T_

 _P

 1

между коэффициентами α_P ,

 _T _P _V

P0V	αV χ	 1
V0	αP

α_Vи χ существует, подтвержденное опытом соотношение: , где P₀,
V₀ – давление и объём газа при 0°С, а V - конечный объём газа при изотермиче- ском процессе.

Воспользуемся уравнением Клапейрона – Менделеева и графиками изо- процессов для нахождения величин α_P , α_Vи χ

1. 
   Изотермический процесс (Т =const,
   

m  const )

Для данной массы газа при постоянной температуре Т = const произведе-

ние давления на объем – величина постоянная

PV =const

или давление газа

изменяется обратно пропорционально объему:

_{P } const

V

, при

m  const, T  const.

График изотермического процесса в координатах (P, ¹ ) - прямая, прохо-

V

дящая через начало координат. Тангенс уг-

ла наклона графика tgγ 

P

ΔP _.


Δ
 ¹ 

 _V

P_с^{ }

Из уравнения состояния идеального га-

P за PV  ^mRT  νRT , имеем для изотерми-

μ

⁰ 1 1 ¹




₁ ческого процесса

P  ^{ 1 }νRT


 
V

, или

^V1 ^Vср ^{V2 V}

 

_ 1 _ dP

dP d_{ }νRT

V

, тогда

 νRT  tgγ .

_ 1 _

  _{d }

R 	tgγ
	νT

Универсальная газовая постоянная равна .

 ^V 

Определим коэффициент всестороннего сжатия

_{χ  } 1 _ V _


 
V P
. Из уравне-

ния состояния имеем
PV  const :
PdV+VdP 0
или



dV _{ } V dP P

_T

. Из уравнения

Клапейрона – Менделеева:

dP  

νRT^dV

_V2

, отсюда

dV _{ }

dP

_V 2


νRT

 χV

. Найдем

коэффициент всестороннего сжатия

χ  

V



P

χ   ¹
νRT

или

χV   ^V , тогда

P

при

Т = const, m  const .

Знак минус в выражении

χ   ¹

P

указывает на то, что увеличение объема

приводит к уменьшению давления. Изотермический коэффициент сжимаемости идеального газа равен, таким образом, обратной величине его давления. С ро- стом давления величина  уменьшается.

графика

Из уравнения состояния идеального газа

PV  ^m RT  νRT , имеем для изо-

μ

барного процесса

PdV  νRdT

или ^dV

R 	Ptgβ
	ν

dT

 ^νR  tgβ , отсюда универсальная газовая

P

постоянная

, где

ν  ^{V V}мол

, а V_мол=22,414 л.

Найдем коэффициент теплового расширения

α_р  <sub>V

</sub> dV_

 _dТ

. Так как

1
₀   _р

^dV  α V

 tgβ , то, учитывая уравнение процесса коэффициент теплового

α  T  tgβ  V V  T 0	1
	T0

_dT P0

V
расширения будет равен α  ^tgβ  ^{T  tgβ} . Так как tgβ  ^νR

, то

при

V₀ VT₀ P

P=const,

m  const ; (T₀=273,15 K).

Описание экспериментальной установки

Экспериментальная установка для исследования экспериментальных газовых законов приведена на рисунке 1.

Рисунок 1. Схема установки для исследования газовых законов.

1. 
   – стеклянный корпус;
   
2. 
   – подвижный поршень (шприц находится внутри стеклянного корпуса);
   
3. 
   – плитка;
   
4. 
   – датчик давления;
   
5. 
   – устройство Cobra;
   
6. 
   – резиновая трубка-переходник;
   

7. 
   ,8 – отверстия в стеклянном корпусе;
   

9. 
   – магнит;
   
10. 
    – термодатчик.
    

В стеклянном корпусе (1) находится шприц с подвижным поршнем (2). Под стеклянным корпусом, не касаясь его, расположена плитка (3). Датчик давления (4), подключают к входу S1 устройства Cobra (5). Короткая резиновая трубка- переходник (6) соединяет датчик давления со шприцом. Этот датчик позволяет ав- томатически производить измерение давления во внутренней камере шприца. Стеклянную емкость через отверстие (7) заполняют водой. В воду помещают маг- нитную мешалку. Можно перемешивать воду, обеспечивая равномерный прогрев воздуха во внутренней камере шприца, поднося магнит (9) к стеклянному корпусу (1). В отверстие (8), закрытое специальной пробкой с отверстием, помещают тер- модатчик (10), также подключив его к разъему S2 устройства Cobra (5).

Осуществить изотермический процесс можно при постоянной температуре, изменяя объем воздуха в шприце, перемещая поршень (2). Давление при этом бу- дет меняться, что автоматически зафиксирует датчик давления (4). Температуру при этом будет фиксировать термодатчик (10).

Изобарический и изохорический процессы можно изучать одновременно. Температуру воздуха в шприце можно увеличить при нагревании воды, находя- щейся в стеклянном корпусе. Для этого используют плитку (3). Нагревание возду- ха в шприце приведет к его расширению, поршень будет перемещаться таким об- разом, чтобы давление оставалось равным атмосферному (р = const). Фиксируя изменение объема воздуха вручную и соответствующую температуру по показа- ниям термодатчика (10), можно получить данные о зависимости V(T) для изоба- рического процесса.

В то же время, можно получить данные о зависимости р(Т) для изохориче- ского процесса, возвращая поршень (2) в исходное положение (к начальному объ- ему, то есть поддерживая V = const) после повышения температуры на определен- ную величину Т (например, 5К). Давление автоматически будет фиксировать датчик давления (4).

Во всех случаях количество воздуха в шприце остается неизменным, то есть  = const.

Порядок выполнения работы

При выполнении работы необходимо строго выполнять требования тех- ники безопасности и охраны труда, установленные на рабочем месте студента в лаборатории.

Лабораторная работа имеет компьютерное сопровождение. Прежде чем приступить к измерениям, изучите правила пользования компьютерной про- граммой.

Внимание! Лабораторная работа состоит из двух частей:

• 
  проверка закона Бойля-Мариотта при комнатной температуре,
  
• 
  проверка законов Гей-Люссака и Шарля при нагревании газа,
  

Подготовка к работе

1. 
   Убедитесь, что установка собрана в соответствии с рис. 1. Не подключайте пока трубку-переходник (6) к датчику давления (4).
   
2. 
   Убедитесь, что, стеклянная емкость заполнена дистиллированной водой и отверстие закрыто крышкой.
   
3. 
   Резиновую трубку, закрепленную на «отростке» отверстия (7), опустите в стеклянный стакан для стекания жидкости при последующем нагревании.
   
4. 
   Перемещая поршень (2), установите начальный объем шприца V_o = 50 мл.
   
5. 
   Подключите трубку (6) к датчику давления (4).
   
6. 
   Устройство Cobra подключено к USB – порту компьютера.
   
7. 
   Включите компьютер.
   
8. 
   Запустите программу для проведения измерений. Для этого на рабочем столе компьютера выберите ярлык программы Phywe Measure 4. В открыв- шемся окне в пункте меню Прибор>Кобра3 Идеальный газ. В появившемся диалоговом окне в закладке Каналы установите настройки измерений в соот- ветствие с рис. 2. Необходимо пройти все вкладки и нажать все нужные флажки.
   

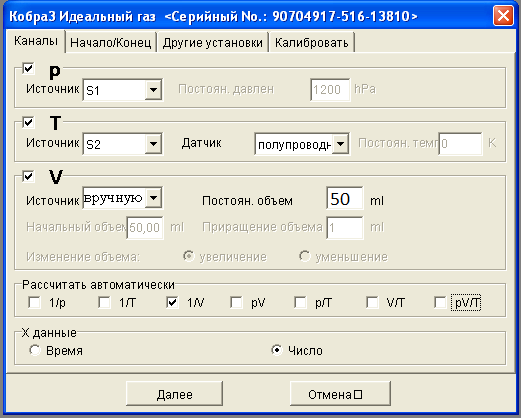
Рисунок 2 Окно настроек работы по изучению изотермического процесса.
В закладке Начало/Конец выберите «по нажатию клавиши».

9. 
   В закладке Другие установки поставьте флажки в поле Цифр. дисплей 1. В появившемся диалоговом окне в разделе Канал выберите Давление р в соот- ветствии с рис. 3а, 3б. Поставьте флажок в поле Цифр. дисплей 2. В появившемся диалоговом окне в разделе Канал выберите Температура Т.
   
10. 
    Поставьте флажок в поле Диаграмма 1, затем в появившемся диалоговом окне Параметры дисплея заполните поля в соответствии с рис. 4. В разделе Ка- нал в поле давление р задается диапазон возможных значений давления. В разде-
    

ле ось х в полях задается число возможных измерений. Рекомендуется в качестве максимального значения выбрать

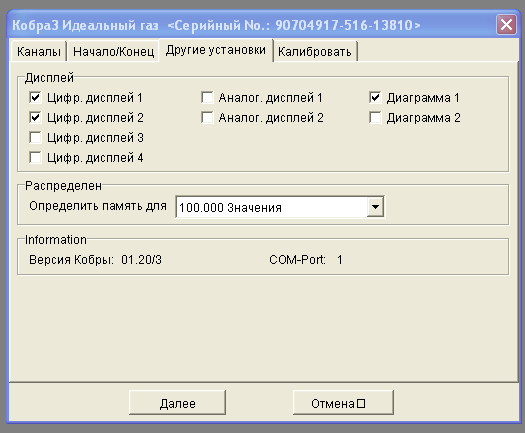Рисунок 3а. Закладке Другие установки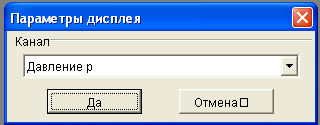

Рисунок 3б. Окно параметры дисплея

11. 
    В поле режим установите не автодиапазон.
    

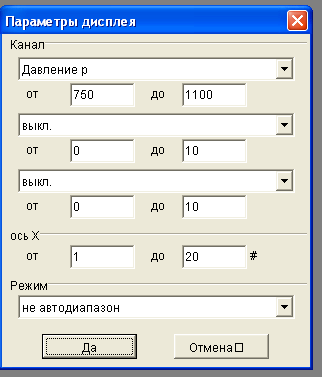Рисунок 4 Окно Параметры дисплея.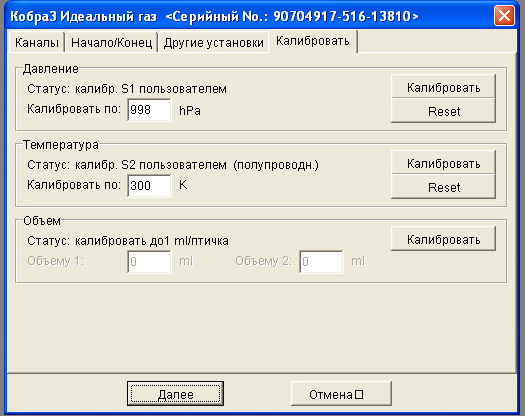

Рисунок 5 Закладка Калибровать

12. 
    Откалибруйте датчик. Для этого в закладке Калибровать введите в соот- ветствующие поля значения комнатной температуры и давления, измеренные термометром и барометром соответственно.
    
13. 
    Нажмите Далее в закладке Калибровать. На экране появится четыре ок- на: температура Т, давление P, Измерение, окно для построения графика зависи- мости давления от числа измерений. Расположите дисплеи, появившиеся на экране, в удобном порядке.
    
14. 
    Сохраните исходные данные измерения температуры Т_о, давления P_о, нажав на кнопку Сохранить значения в окне Измерения (рис. 6) или Enter.
    

15. 
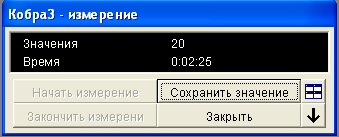
    Рисунок 6 Окно Измерения.
    

Упражнение 1. Проверка закона Бойля – Мариотта при комнатной тем-

пературе

1. 
   Рассчитайте число молей воздуха в шприце (V₁ – начальный объем воздуха, равный 50 мл)
   
2. 
   Перемещая вращательным движением поршень (2) шприца вправо, уве- личьте объем на 1 мл. Давление воздуха в шприце изменится.
   
3. 
   Постепенно увеличивайте объем воздуха с шагом в 1 мл до объема при- близительно в 60 мл. Результаты измерений занести в таблицу №1.
   
4. 
   Постройте график зависимости P=f(V)
   
5. 
   Убедитесь, что график зависимости P=f(V) действительно является ги- перболой. Для этого линеаризируйте его, построив график зависимости P=f(1/V).
   
6. 
   Рассчитайте тангенс угла наклона  полученного графика. Определите универсальную газовую постоянную R и модуль всестороннего сжатия χ.
   

Упражнение 2. Проверка законов Гей-Люссака и Шарля при нагрева-

нии газа

1. 
   Перемещая поршень (2), установите начальный объем шприца V₁ = 50 мл. и установите начальное давление, для этого отсоедините датчик давления и потом подсоедините его обратно.
   
2. 
   Запишите исходные данные измерения температуры Т₁, давления P₁ в от-
   

чет.

3. 
   Рассчитайте число молей воздуха в шприце.
   

4. Включите нагреватель.

Примечание: В процессе измерений не забывайте перемешивать воду в

стеклянном корпусе, поднося к нему магнитную мешалку

Внимание: пп. 5, 6 выполняются одновременно.

5. 
   После каждого увеличения температуры примерно на Т = 5 К, перемещая поршень шприца вращательным движением, доводите объем в шприце до началь- ного V₁ и заносите результаты измерения давления и температуры в таблицу №2 (изохорный процесс).
   
6. 
   После каждого увеличения объема воздуха в шприце на 1 мл фиксируйте этот объем и соответствующее ему значение температуры и записываем в таблицу
   

№3. Завершите измерения после достижения объема воздуха 60 мл (изобарный процесс).

7. 
   Постройте график зависимости V=f(T). Рассчитайте объем воздуха V_o, соответствующий температуре 0^оС.
   
8. 
   Рассчитайте тангенс угла наклона полученного графика. Определите универсальную газовую постоянную R и коэффициент теплового расширения α_V.
   
9. 
   Постройте график зависимости P=f(Т). По графику зависимости P=f(Т).
   

экстраполяцией в область значений Т=273К найдите значение P₀.

10. 
    Рассчитайте тангенс угла наклона полученного графика. Определите универсальную газовую постоянную R и термический коэффициент давления α_P.
    
11. 
    Проведите статистическую обработку результатов измерений R, полу-
    

ченных разными способами и сравните коэффициенты α_V и α_P . Определите их

теоретическое значение:

α = α = ¹

, (T₀=273,15K).

T
P V

0

Список литературы

1. 
   Матвеев А.Н. Молекулярная физика. – М. Высшая школа, 2011.
   
2. 
   Кикоин А.К., Кикоин И.К. Молекулярная физика. – М.: Наука, 2006.
   
3. 
   Сивухин Д.В.Общий курс физики. – М.: Наука, 2000, Т.2.
   
4. 
   Иродов И.Е. Физика макросистем. – М.: Наука, 2004.
   
5. 
   Гершензон Е.М., Малов Н.Н., Мансуров А.Н. Молекулярная физика. – М.: АСАDEMA, 2000.
   
6. 
   Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, т. 2, 3. 2011.
   
7. 
   Трофимова Т. И. Курс физики. – М.: Высшая школа, 2008.
   
8. 
   Савельев И. В. Курс общей физики. – М.: Наука, 2007. Т. 1.
   

Контрольные вопросы

1. 
   Какой газ называется идеальным? При каких условиях реальный газ можно считать идеальным?
   
2. 
   Напишите уравнения состояния для идеального газа?
   
3. 
   Сформулируйте закон Бойля – Мариотта? Каким уравнением он описыва- ется?
   
4. 
   Сформулируйте закон Гей-Люссака? Каким уравнением он описывается?
   
5. 
   Сформулируйте закон Шарля? Каким уравнением он описывается?
   
6. 
   Каков физический смысл термического коэффициента давления? Как в данной работе он определяется?
   
7. 
   Каков физический смысл термического коэффициента объемного расши- рения? Как в данной работе он определяется?
   
8. 
   Каков смысл коэффициента всестороннего сжатия? Как в данной работе он определяется?
   
9. 
   Как связаны между собой коэффициенты объемного расширения, термиче- ский коэффициент давления и коэффициент всестороннего сжатия?
   
10. 
    Выведите законы изопроцессов из уравнения состояния идеального газа.
    
11. 
    Изобразите графики изопроцессов в координатах P(V), V(T), P(T).
    
12. 
    Выведите формулы для расчета универсальной газовой постоянной, ис- пользуя графики изопроцессов.
    
13.