Главная страница
Навигация по странице:

  • 1.Проведение полного факторного эксперимента (ПФЭ)

  • 2.Проведение ортогонального центрального композиционного планирования (ОЦКП)

  • 3. Сводная таблица результатов нахождения коэффициентов

  • 4. Результаты нахождения оптимального центра плана (ОЦКП)

    		•

    Вариант6. Лабораторная работа 4 Обработка результатов активных экспериментов студентка Москва, 2017


    Скачать 36.59 Kb.
    НазваниеЛабораторная работа 4 Обработка результатов активных экспериментов студентка Москва, 2017
    Дата19.03.2018
    Размер36.59 Kb.
    Формат файлаdocx
    Имя файлаВариант6.docx
    ТипЛабораторная работа
    #38870


    ЛАБОРАТОРНАЯ РАБОТА № 4

    «Обработка результатов активных экспериментов»

    Выполнила: студентка

    Москва, 2017

    Вариант №6

    Необходимо подобрать оптимальные значения температуры и времени превращения четырехстадийной реакции

    А Р S
    Q

    при которых концентрация промежуточного продукта была бы максимальной.

    Задан центр планирования: Тц.п. = 330 К – температура проведения реакции; tц.п. = 75 с – время проведения реакции; интервал изменения параметров соответственно: DТ = ±10 К;  = ± 25 с.

    I. Полный факторный эксперимент (ПФЭ) включает опыты 1÷4 и эксперименты в центре плана – опыты 9÷14 (330 К, 75 с) – для определения дисперсии воспроизводимости .

    На основании экспериментальных данных определить:

    A) Коэффициенты линейного уравнения регрессии C = 0 + 1T + 2 для компонента реакции (например, Р):

    0; 1; 2.

    Б) Проверить значимость коэффициентов уравнения регрессии.

    B) Проверить адекватность уравнения регрессии.

    II. Ортогональное центральное композиционное планирование позволяет найти координаты оптимальных значений факторов. Эксперимент дополняется опытами в звёздных точках факторного пространства: точками 5÷6 с координатами (Тц.п. ± DТ; tц.п.) и точками 7÷8 с координатами с координатами (Тц.п.; tц.п. + D); где  –звёздное плечо.

    На основании экспериментальных данных определить:

    A) Коэффициенты нелинейного уравнения C = 0 + 1T + 2 + 12T + 11T2 + 222 для компонента реакции (например, Р):

    0; 1; 2; 12; 11; 22.

    Б) Проверить значимость коэффициентов уравнения регрессии.

    B) Проверить адекватность уравнения регрессии.

    Г) Найти координаты (Тopt ; topt) экстремальной точки функции С = f(T, t).

    Результаты эксперимента:


    №
    Т, К
    , с
    СА
    СP
    СS
    СQ

    1
    320
    50
    0,1203
    0,0475
    0,3957
    0,4365

    2
    340
    50
    0,015
    0,0024
    0,8733
    0,11

    3
    320
    100
    0,064
    0,026
    0,438
    0,472

    4
    340
    100
    0,0073
    0,0013
    0,897
    0,095

    5
    316,8
    75
    0,1178
    0,0498
    0,3262
    0,5061

    6
    343,2
    75
    0,007
    0,001
    0,9206
    0,0714

    7
    330
    42
    0,0492
    0,014
    0,6786
    0,2582

    8
    330
    108
    0,0197
    0,0058
    0,7237
    0,2508

    9
    330
    75
    0,0298
    0,008
    0,6669
    0,2681

    10
    330
    75
    0,0271
    0,0084
    0,7111
    0,2488

    11
    330
    75
    0,0287
    0,0087
    0,7308
    0,243

    12
    330
    75
    0,0274
    0,0083
    0,6893
    0,2644

    13
    330
    75
    0,0292
    0,0076
    0,7238
    0,2562

    14
    330
    75
    0,0279
    0,0083
    0,7494
    0,2549

    1.Проведение полного факторного эксперимента (ПФЭ)
    Программа PFE:

    global ce;global Tcp;global taucp;global n;global nc;global N

    global ysrcp;global Se2;global Se;global ttabl

    %Обработка результатов ПФЭ

    disp(sprintf('Обработка результатов ПФЭ'));

    %Координаты ц.п.(по усл.)

    Tcp=330;taucp=75;

    %изменения температуры и времени (по усл.)

    dT=10;dtau=25;

    %число опытов ПФЭ

    n=4;

    %число опытов в ц.п.

    nc=6;

    %Общее число опытов (в данной работе необходимо для ввода массива экспериментальных данных)

    N=14;

    disp(sprintf('Экспериментальные значения концентраций проможеточного продукта'));

    for i=1:N

    disp(sprintf('Номер эксперимента i=%G',i));

    ce(i)=input('ce=');

    end

    for j=1:8

    DEISTV=j;

    if DEISTV==1

    disp(sprintf('Матрица z и вектор ye'));

    %Матрица планирования ФПЭ (у всех одинакова)

    z=[1 -1 -1;1 1 -1;1 -1 1;1 1 1];

    %Вектор наблюдений

    ye=[ce(1);ce(2);ce(3);ce(4)];

    disp('z=');disp(z)

    disp('ye=');disp(ye)

    disp(sprintf('Если Вы хотите переходить к следующему действию расчёту коэффициентов уравнения регрессии введите Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==2

    disp(sprintf('Расчёт коэффициентов уравнения регрессии по фр-ле 4.244'));

    %Нахождение числителя уравнения 4.244

    s1=0;s2=0;s3=0;

    for i=1:n

    sum1(i)=z(i,1);sum2(i)=z(i,2);sum3(i)=z(i,3);

    s1=s1+sum1(i)*ye(i);

    s2=s2+sum2(i)*ye(i);

    s3=s3+sum3(i)*ye(i);

    end

    %Кодированные коэффициенты уравнения регрессии находятся по уравнению 4.244

    ak0=s1/n;

    ak1=s2/n;

    ak2=s3/n;

    disp(sprintf('кодированные коэфф. ур. регрессии'));

    disp(sprintf('ak0=%G ak1=%G ak2=%G',ak0,ak1,ak2));

    ak=[ak0 ak1 ak2];

    disp(sprintf('Если Вы хотите переходить к следующему действию - расчёту дисперсии воспроизводимости введите Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==3

    disp(sprintf('Расчёт дисперсии воспроизводимости'));

    %Среднее арифметическое измерений во всех параллельных опытах

    ysrcp=(ce(9)+ce(10)+ce(11)+ce(12)+ce(13)+ce(14))/nc;

    disp(sprintf('Среднее арифметическое измерений во всех параллельных опытах ysrcp=%G',ysrcp));

    %Дисперсия воспроизводимости по результатам параллельных опытов в ц.п.

    Se2=((ce(9)-ysrcp)^2+(ce(10)-ysrcp)^2+(ce(11)-ysrcp)^2+(ce(12)-ysrcp)^2+(ce(13)-ysrcp)^2+(ce(14)-ysrcp)^2)/(nc-1);

    disp(sprintf('Дисперсия воспроизводимости Se2=%G',Se2));

    Se=sqrt(Se2);

    disp(sprintf('Если Вы хотите переходить к следующему действию - Проверкe значимости кодированных коэффициентов уравнения регрессии введите Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==4

    disp(sprintf('Проверка значимости кодированных коэффициентов уравнения регрессии'));

    %Табличный критерий Стьюдента

    ttabl=2.571;

    %Расчётный критерий Стьюдента и оценка значимостей коэффициентов ур. регрессии

    for u=1:length(ak)

    t(u)=abs(ak(u))*sqrt(n)/Se;

    disp(sprintf('u=%G t(u)=%G',u,t(u)));

    %Проверка значимости кодированных коэффициентов уравнения регрессии

    if t(u)
    disp(sprintf('Коэффициент незначим'));

    else

    disp(sprintf('Коэффициент значим'));

    end

    end

    %Количество значимых коэффициентов ур. регрессии вводится интерактивно

    disp(sprintf('Количество значимых коэффициентов уравнения регрессии'));

    p=input('p=');

    disp(sprintf('Если Вы хотите переходить к следующему действию - расчёту остаточной дисперсии введите Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==5

    disp(sprintf('Расчёт остаточной дисперсии'));

    %Расчёт остаточной дисперсии

    s=0;

    for i=1:n

    yeksp(i)=ce(i);

    y(i)=ak0+ak1*z(i,2)+ak2*z(i,3);

    disp(sprintf('z1=%G z2=%G y(i)=%G yeksp(i)=%G',z(i,2),z(i,3),y(i),yeksp(i)));

    SS(i)=(y(i)-yeksp(i))^2;

    s=s+SS(i);

    end

    Sr2=s/(n-p);

    disp(sprintf('Остаточная дисперсия Sr2=%G',Sr2));

    disp(sprintf('Если Вы хотите переходить к следующему действию - расчёту Критерия Фишера Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==6

    disp(sprintf('Расчёт Критерия Фишера'));

    %Расчётный критерий Фишера

    Fr=Sr2/Se2;

    disp(sprintf('Расчётный критерий Фишера Fr=%G',Fr));

    disp(sprintf('Если Вы хотите переходить к следующему действию - установлению адекватности уравнения регресии Signal=1 иначе Signal=2'));

    end

    if Signal==2 break; end

    if DEISTV==7

    disp(sprintf('Установление адекватности уравнения регрессии'));

    Ft=input('Ft=');

    if Fr<=Ft

    disp(sprintf('Уравнение регрессии адекватно'));

    else

    disp(sprintf('Уравнение регрессии неадекватно'));

    end

    disp(sprintf('Если Вы хотите переходить к следующему действию - расчёту некодированных коэффициентов уравнения регресии Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==8

    disp(sprintf('Переход к некодированным коэффициентам'));

    %Переход к некодированным коэффициентам

    Teta0=ak0-(ak1*Tcp/dT)-(ak2*taucp/dtau);

    Teta1=ak1/dT;

    Teta2=ak2/dtau;

    disp(sprintf('некодированные коэфф. ур. регрессии'));

    disp(sprintf('Teta0=%G Teta1=%G Teta2=%G',Teta0,Teta1,Teta2));

    end

    end

    Матрица z и вектор ye

    z= 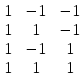ye=

    2.Проведение ортогонального центрального композиционного планирования (ОЦКП)

    ПрограммаОЦКП:

    global ce;global Tcp;global taucp;global n;global nc;global N

    global ysrcp;global Se2;global Se;global ttabl

    %Обработка результатов ОЦКП

    disp(sprintf('Обработка результатов ОЦКП'));

    %некоторая постоянная величина, обеспечивающая ортогональность матрицы z

    S=sqrt(n/N);

    %Звёздное плечо

    alfa=(0.5*n*(sqrt(N/n)-1))^0.5;

    disp(sprintf('alfa=%G S=%G',alfa,S));

    for j=1:8

    DEISTV=j;

    if DEISTV==1

    %Матрица планирования ОЦКП

    z=[1 -1 -1 1 1-S 1-S;1 1 -1 -1 1-S 1-S;1 -1 1 -1 1-S 1-S;1 1 1 1 1-S 1-S;1 -alfa 0 0 alfa*alfa-S -S;1 alfa 0 0 alfa*alfa-S -S;1 0 -alfa 0 -S alfa*alfa-S;1 0 alfa 0 -S alfa*alfa-S;1 0 0 0 -S -S;1 0 0 0 -S -S;1 0 0 0 -S -S;1 0 0 0 -S -S;1 0 0 0 -S -S;1 0 0 0 -S -S];

    disp('z=');disp(z);

    %Вектор наблюдений

    ye=ce';

    disp('ye=');disp(ye);

    disp(sprintf('Если Вы хотите переходить к следующему действию расчёту коэффициентов уравнения регрессии введите Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==2

    disp(sprintf('Расчёт коэффициентов уравнения регрессии по фр-лaм 4.278-4.281'));

    %Нахождение числителей уравнений 4.278-4.281

    s1=0;s2=0;s3=0;s4=0;s5=0;s6=0;

    for i=1:N

    sum2(i)=z(i,2);sum3(i)=z(i,3);sum4(i)=z(i,4);sum5(i)=z(i,5);sum6(i)=z(i,6);

    s1=s1+ye(i);

    s2=s2+sum2(i)*ye(i);

    s3=s3+sum3(i)*ye(i);

    s4=s4+sum4(i)*ye(i);

    s5=s5+sum5(i)*ye(i);

    s6=s6+sum6(i)*ye(i);

    end

    %Нахождение кодированных коэффициентов регрессии по уравнениям 4.278-4.281

    ak0=s1/N;

    ak1=s2/(n+2*alfa^2);

    ak2=s3/(n+2*alfa^2);

    ak12=s4/(n);

    ak11=s5/(2*alfa^4);

    ak22=s6/(2*alfa^4);

    disp(sprintf('коэфф. ур. регрессии'));

    disp(sprintf('ak0=%G ak1=%G ak2=%G ak12=%G ak11=%G ak22=%G',ak0,ak1,ak2,ak12,ak11,ak22));

    disp(sprintf('Если Вы хотите переходить к следующему действию - Проверкe значимости кодированных коэффициентов уравнения регрессии введите Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==3

    disp(sprintf('Проверка значимости кодированных коэффициентов уравнения регрессии'));

    %Проверка значимости кодированных коэффициентов уравнения регрессии

    %Расчётный критерий Стьюдента и оценка значимостей коэффициентов ур.регр.

    t0=abs(ak0)*sqrt(N)/Se; disp(sprintf('t0=%G',t0));

    if t0
    disp(sprintf('Коэффициент ak0 незначим'));

    else

    disp(sprintf('Коэффициент ak0 значим'));

    end

    t1=abs(ak1)*sqrt(n+2*alfa^2)/Se;disp(sprintf('t1=%G',t1));

    if t1
    disp(sprintf('Коэффициент ak1 незначим'));

    else

    disp(sprintf('Коэффициент ak1 значим'));

    end

    t2=abs(ak2)*sqrt(n+2*alfa^2)/Se;disp(sprintf('t2=%G',t2));

    if t2
    disp(sprintf('Коэффициент ak2 незначим'));

    else

    disp(sprintf('Коэффициент ak2 значим'));

    end

    t12=abs(ak12)*sqrt(n)/Se;disp(sprintf('t12=%G',t12));

    if t12
    disp(sprintf('Коэффициент ak12 незначим'));

    else

    disp(sprintf('Коэффициент ak12 значим'));

    end

    t11=abs(ak11)*sqrt(2*alfa^4)/Se;disp(sprintf('t11=%G',t11));

    if t11
    disp(sprintf('Коэффициент ak11 незначим'));

    else

    disp(sprintf('Коэффициент ak11 значим'));

    end

    t22=abs(ak22)*sqrt(2*alfa^4)/Se;disp(sprintf('t22=%G',t22));

    if t22
    disp(sprintf('Коэффициент ak22 незначим'));

    else

    disp(sprintf('Коэффициент ak22 значим'));

    end

    disp(sprintf('Количество значимых коэффициентов уравнения регрессии'));

    p=input('p=');

    disp(sprintf('Если Вы хотите переходить к следующему действию - расчёту остаточной дисперсии введите Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==4

    %Расчёт остаточной дисперсии

    disp(sprintf('Расчёт остаточной дисперсии'));

    s=0;

    for i=1:N

    yeksp(i)=ce(i);

    z1=z(i,2);z2=z(i,3);

    y(i)=ak0+ak1*z1+ak2*z2+ak12*z1*z2+ak11*(z1^2-S)+ak22*(z2^2-S);

    disp(sprintf('i=%G z1=%G z2=%G y(i)=%G yeksp(i)=%G',i,z1,z2,y(i),yeksp(i)));

    SS(i)=(y(i)-yeksp(i))^2;

    s=s+SS(i);

    end

    Sr2=s/(N-p);

    disp(sprintf('Остаточная дисперсия Sr2=%G',Sr2));

    disp(sprintf('Если Вы хотите переходить к следующему действию - расчёту Критерия Фишера Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==5

    disp(sprintf('Расчёт Критерия Фишера'));

    %Расчётный критерий Фишера

    Fr=Sr2/Se2;

    disp(sprintf('Расчётный критерий Фишера Fr=%G',Fr));

    disp(sprintf('Если Вы хотите переходить к следующему действию - установлению адекватности уравнения регресии Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==6

    disp(sprintf('Установление адекватности уравнения регрессии'));

    Ft=input('Ft=');

    if Fr<=Ft

    disp(sprintf('Уравнение регрессии адекватно'));

    else

    disp(sprintf('Уравнение регрессии неадекватно'));

    end

    disp(sprintf('Если Вы хотите переходить к следующему действию - расчёту некодированных коэффициентов уравнения регресии Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==7

    disp(sprintf('Переход к некодированным коэффициентам'));

    %Переход к некодированным коэффициентам ур. регрессии

    Teta0=ak0-(ak1*Tcp/dT)-(ak2*taucp/dtau)+(ak12*Tcp*taucp/(dT*dtau))+(ak11*Tcp^2/dT^2)-ak11*S+(ak22*taucp^2/dtau^2)-ak22*S;

    Teta1=(ak1/dT)-(ak12*taucp/(dT*dtau))-2*ak11*Tcp/dT^2;

    Teta2=(ak2/dtau)-(ak12*Tcp/(dT*dtau))-2*ak22*taucp/dtau^2;

    Teta12=ak12/(dT*dtau);

    Teta11=ak11/(dT^2);

    Teta22=ak22/(dtau^2);

    disp(sprintf('некодированные коэфф. ур. регрессии'));

    disp(sprintf('Teta0=%G Teta1=%G Teta2=%G Teta12=%G Teta11=%G Teta22=%G',Teta0,Teta1,Teta2,Teta12,Teta11,Teta22));

    disp(sprintf('Если Вы хотите переходить к следующему действию - нахождению экстремума ф-ции отклика Signal=1 иначе Signal=2'));

    Signal=input('Signal=');

    end

    if Signal==2 break; end

    if DEISTV==8

    disp(sprintf('Нахождение экструмума ф-ции отклика'));

    %Применение уравнения II порядка

    A=[2*ak11 ak12;ak12 2*ak22];

    b=[-ak1;-ak2];

    %СЛАУ решается методом обратной матрицы

    Aobr=inv(A);

    zopt=Aobr*b;

    disp(sprintf('Координаты экстремума функции отклика в кодированной системе координат'));

    disp('zopt=');disp(zopt);

    %Нахождение оптимальной температуры и оптимального времени

    Topt=dT*zopt(1)+Tcp;

    tauopt=dtau*zopt(2)+taucp;

    disp(sprintf('Topt=%G tauopt=%G',Topt,tauopt));

    end

    end

    Матрица z и вектор ye

    z=

    ye=
    3. Сводная таблица результатов нахождения коэффициентов

    №
    a
    Коэффициенты уравнения регрессии
    S2R
    S2e
    FP
    FT
    Заключение

    1
    a0=0.0193

    a1=(-0.01745)

    a2=(-0.00565)

    tp0=102.554

    tp1=92.7239

    tp2=30.0223
    Θ0=0.6121

    Θ1=(-0.001745)

    Θ2=(-0.000226)
    0.00010404
    1.41667E-07
    734.4
    3.0123
    уравнение регрессии неадекватно

    2
    a0=0.0140786

    a1=(-0.0179335)

    a2=(-0.00446616)

    a12=0.0051

    a11=0.00994303

    a22=0.00104347

    tp0=139.955

    tp1=130.34

    tp2=32.4599

    tp12=27.0998

    tp11=65.0673

    tp22=6.82845
    Θ0=11.9557

    Θ1=(-0.0689474)

    Θ2=(-0.00716108)

    Θ12=2.04E-05

    Θ11=9.94303E-05

    Θ22=1.66954E-06
    1.85857E-06



    13.1193
    3.5005
    уравнение регрессии неадекватно

    И для ПФЭ, и для ОЦКП все кодированные коэффициенты уравнения регрессии являются значимыми.

    4. Результаты нахождения оптимального центра плана (ОЦКП)

    Zopt =

    Topt = 339.456

    τopt = 70.7287

    5. Заключение

    В ходе работы проведена обработка результатов активного эксперимента, в результате которой были найдены необходимые коэффициенты и параметры для определения адекватности уравнений регрессии, найден оптимальный центр плана (для ОЦКП). В обоих случаях уравнения оказались неадекватными.

    написать администратору сайта