ПРОВЕРКА ТАБЛИЦЫ ИСТИННОСТИ ОСНОВНЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ. Лабораторная работа 4 По дисциплине Электроника На тему " проверка таблицы истинности основных логических элементов "

• Название: Лабораторная работа 4 По дисциплине Электроника На тему " проверка таблицы истинности основных логических элементов "
• Анкор: ПРОВЕРКА ТАБЛИЦЫ ИСТИННОСТИ ОСНОВНЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
• Дата: 13.10.2022
• Размер: 106.99 Kb.
• Имя файла: ПРОВЕРКА ТАБЛИЦЫ ИСТИННОСТИ ОСНОВНЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ.docx
• Тип: Лабораторная работа; #732451

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН КАРАГАНДИНСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИМЕНИ АБЫЛКАСА САГИНОВА

Кафедра автоматизации производственных процессов им. проф. В.Ф. Бырьки

 

 
 

Лабораторная работа №4
По дисциплине: «Электроника»

На тему: “ПРОВЕРКА ТАБЛИЦЫ ИСТИННОСТИ ОСНОВНЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ”

 

 

 

 


 

 

 

Выполнил :студент ЭЭ-20-4

Якименко Антон

Проверил: ст. препод.

Потемкина Е.Б

 

 

 

 
Лабораторная работа № 1. ПРОВЕРКА ТАБЛИЦЫ ИСТИННОСТИ ОСНОВНЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ

1. 
   Цель работы: Целью лабораторной работы является экспериментальное получение таблиц соответствия (таблиц истинности) логических элементов И (AND), НЕ (NOT), ИЛИ (OR), И-НЕ (NOT-AND), ИЛИ-НЕ (NOT-OR), Исключающее ИЛИ (XOR), Исключающее ИЛИ-НЕ (XNOR).
   

2. Краткие сведения из теории

Математической основой цифровых вычислительных устройств является двоичная арифметика, в которой используется всего два числа – 0 и 1. Выбор двоичной системы счисления диктовался требованиями простоты технической реализации самых сложных задач с использованием всего одного базового элемента – ключа, который имеет два состояния: включен (замкнут) или выключен (разомкнут). Если первое состояние ключа принять за условную (логическую) единицу, то второе будет отражать условный (логический) ноль или наоборот.

Логическая переменная – некоторая переменная величина X, которая может принимать одно из двух значений 0 или 1, то есть быть ложной или истинной X={0,1}.

Логическая функция (булева функция, переключательная функция, функция алгебры логики) n переменных – это функция, которая может принимать одно из двух значений 0 или 1 на некотором наборе этих переменных F (X₁, X₂,…,X_n) ={0,1}.

Логическая функция задается таблицей истинности.

Таблица истинности – это совокупность всех возможных наборов (комбинаций) логических переменных и значений функции на этих наборах.

Термин «логика» происходит от древнегреческого «logos», означающего «слово, мысль, понятие, рассуждение, закон».

Итак, переменные, рассматриваемые в алгебре логики, могут принимать только два значения – 0 или 1.

В алгебре логики определены: отношение эквивалентности (F=A), и операции:

• 
  логического сложения (дизъюнкции) (ИЛИ) F=А+В;
  
• 
  логического умножения (конъюнкции) (И) F=А*В;
  
• 
  отрицания (инверсии) (НЕ) F= А;
  
• 
  логического сложения с инверсией (функция Пирса) (ИЛИ–НЕ) F= А  В ;
  
• 
  логического умножения с инверсией (функция Шеффера) (И–НЕ) F= А* В ;
  
• 
  неравнозначности (исключающее ИЛИ) F= ^{А* В}+ ^А*В=А В;
  
• 
  равнозначности (исключающее ИЛИ-НЕ) F= А* В A* B= А В.
  

В приведенных выше функциях входными переменными являются Аи

В, выходной – переменная F.

Каждой из этих функций соответствует свой логический элемент.

На рисунке 1.1 приведены 2-входовые логические элементы (исключение элемент «НЕ», у него 1 вход), используемые в ППП PROTEUS ISIS 7.

Все логические элементы могут иметь любое количество входов и описываться аналогичными функциями, например, работу 3-х входового элемента «ИЛИ» (3ИЛИ) можно описать функцией F=A+B+C. Исключением является элемент «НЕ», который всегда имеет только 1 вход.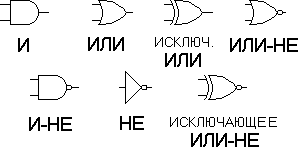

Рисунок 1.1 – Графическое обозначение логических элементов
Данные обозначения элементов применяются в западных странах. В отечественной же промышленности применяют обозначения, показанные на рисунке 1.2.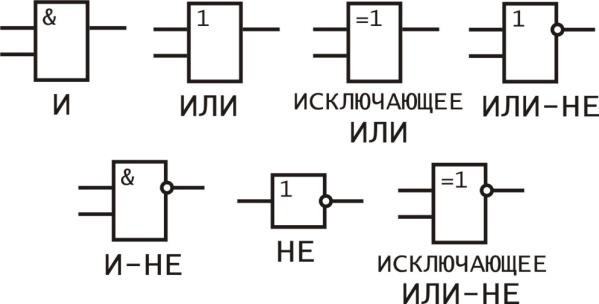



Рисунок 1.2 – УГО логических элементов
Так как область определения любой двоичной функции N-переменных конечна (2ⁿ - значений), такая функция может быть задана таблицей

значений F(x_i), которые она принимает в точках x_i, где i=0,1,2,.. 2^n-1 – номер опыта. Такие таблицы называют таблицами истинности (таблица 1.1).

Таблица 1.1 Таблица истинности двухвходового элемента

i	X1	X0	F(xi)
0	0	0
1	0	1
2	1	0
3	1	1

3. Содержание лабораторной работы Задание:

1. 
   Исследовать логические функции И, НЕ, ИЛИ, И-НЕ, ИЛИ-НЕ, исключающее ИЛИ, исключающее ИЛИ-НЕ, используя типовые компоненты ППП PROTEUS ISIS 7.
   
2. 
   Заполнить таблицу истинности логических функций от двух переменных (таблица 1.2).
   

Таблица 1.2 Бланк для заполнения таблицы истинности

i	А	В	F=А*В	F= А* В	F=А+В	F= А В	F=А  В	F= А В
0	0	0	0	1	0	1	0	1
1	0	1	0	1	1	0	1	0
2	1	0	0	1	1	0	1	0
3	1	1	1	0	1	0	0	1

Порядок выполнения:

1. 
   Загрузить ППП PROTEUS ISIS 7.
   
2. 
   Реализовать на ключах и логических элементах типовые логические функции, представленные на рисунках 1.3…1.8.
   
3. 
   Результаты исследования занести в таблицу 1.2.
   

Рисунок 1.3 – Логическая функция – «И»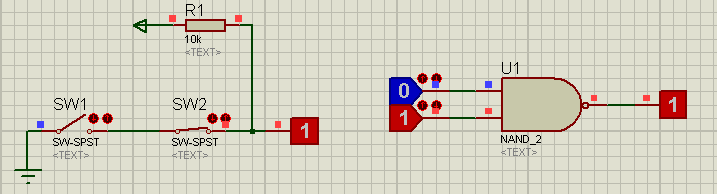


Рисунок 1.4 – Логическая функция – «И–НЕ»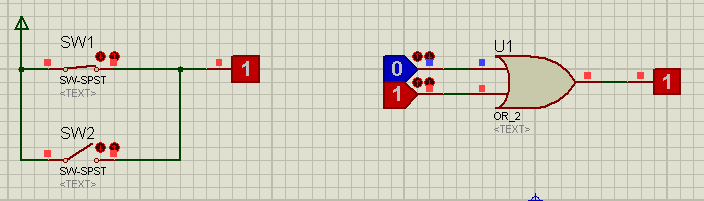



Рисунок 1.5 – Логическая функция – «ИЛИ»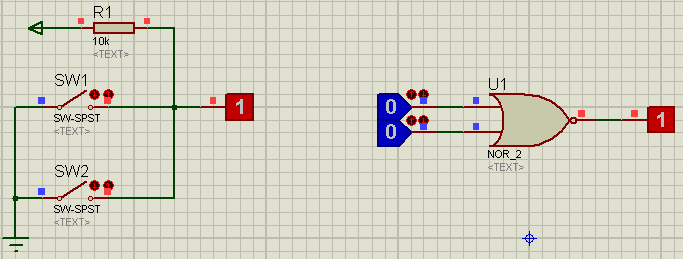




Рисунок 1.6 – Логическая функция – «ИЛИ–НЕ»



Рисунок 1.7 – Логическая функция –

«Исключающее–ИЛИ» (Неравнозначность)


Рисунок 1.8 – Логическая функция – «Исключающее–ИЛИ-НЕ» (Равнозначность)

Контрольные вопросы

1. 
   Переменные могут принимать в алгебре логики только два значения: истина(1) и ложь (1)
   
2. 
   В качестве основных логических операций в сложных логических выражениях используются следующие: НЕ (логическое отрицание, инверсия); ИЛИ (логическое сложение, дизъюнкция); И (логическое умножение, конъюнкция).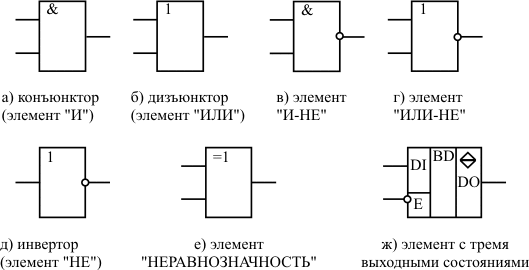
   
3. 
   
   

4. 
   У элемента " НЕ" есть только один вход, "И-НЕ","ИЛИ- НЕ" Данные логические элементы объединяет то, что они имеют несколько равноправных входов (от 2 до 12), а выход всего один.
   

5. 
   “И” может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
   

«ИЛИ» так же как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом
«Исключающее ИЛИ» - логический элемент, выполняющий над входными данными операцию логического сложения по модулю 2, имеет два входа и один выход

Список рекомендуемой литературы Основная

1. 
   Бойко В.И., Гурджий А.Н., Жуков В.Я. и др. Схемотехника электронных устройств. Микропроцессоры и микроконтроллеры. СПб.:БХВ – Петербург, 2004. – 464 с.
   
2. 
   Угрюмов Е.П. Цифровая схемотехника. СПб.:БХВ – Петербург, 2000. – 528 с.
   
3. 
   Бирюков С.А. Применение цифровых микросхем серии ТТЛ и КМОП. 2-е изд. – М.: ДМК, 2000. – 240 с.
   
4. 
   Калабеков Л.А. Цифровые устройства и микропроцессорные системы. 2-е изд. – М.: Горячая линия–Телеком, 2005. – 336 с.
   
5. 
   Букреев И.Н., Горячев В.И., Мансуров Б.М. Микроэлектронные схемы цифровых устройств. – М.: Техносфера, 2009. – 712 с.
   
6. 
   Уилкинсон Барри. Основы построения цифровых систем.: Пер. с англ. – М: Изд. Дом «Вильямс», 2006. 320 с.
   
7. 
   Джонсон Говард, Грэхем Мартин. Конструирование высокоскоростных цифровых устройств.: Пер. с англ. – М: Изд. Дом
   

«Вильямс», 2006. – 624 с.

8. 
   Музылёва И.В. Элементная база для построения цифровых систем управления. – М.: Техносфера, 2006. – 144 с.
   
9. 
   Пухальский Г.И., Новосельцева Т.Я. Цифровые устройства. Учебное пособие для втузов. – СПб.: Политехника, 2001. – 885 с.
   
10. 
    Пухальский Г.И. Проектирование микропроцессорных систем. Учебное пособие для втузов. – М.: Радио и связь, 2001. – 544 с
    
11. 
    Карлащук В.И. Электронная лаборатория на IBM PC. Лабораторный практикум на базе Electronics Workbench и Matlab. – М.: СОЛОН-Пресс, 2004. – 800 с.
    
12. 
    М. Предко. Руководство по микроконтроллерам. Том I. .: Пер. с англ. Москва: Постмаркет, 2001.- 416с.
    
13. 
    М. Предко. Руководство по микроконтроллерам. Том II. .: Пер. с англ. Москва: Постмаркет, 2001.- 488с.
    

Дополнительная

14. 
    Техническая документация DS30292C компании Microchip Technology Incorporated, USA. PIC 16F87X. Однокристальные 8- разрядные FLASH CMOS микроконтроллеры компании Microchip Technology Incorporated.: Пр. с англ.– М.:ООО «Микро-Чип», 2002.–184с.
    
15. 
    Фирма «Microchip» Справочник по среднему семейству микроконтроллеров PICmicroТМ ООО «Микрочип». Москва – 2002.
    
16. 
    Яценков В.С. Микроконтроллеры Microchip. Практическое руководство. М.: Горячая линия–Телеком, 2002. – 296 с.
    
17. 
    Тавернье К. «PIC – MK. Практика применения»: перевод с фр. – М.: ДМК Пресс 2002г. -272с.
    
18. 
    Анна и Манфред Кёнинг. Полное руководство по PIC- микроконтроллерам. PIC18, PIC10F, rfPIC. Киев: МК-Пресс, 2007 – 255с.
    
19. 
    Гелль, П. Электронные устройства с программируемыми компонентами. М.:ДМК Пресс, 2001.
    
20. 
    Шпак Ю.А. Программирование на языке С для AVR и PIC микроконтроллеров. Киев: МК-Пресс, 2006 – 400с
    
21. 
    Бородин В.Б., Калинин А.В., Системы на микроконтроллерах и БИС программируемой логики. – М.: Издательство ЭКОМ, 2002– 400с.:илл.
    

КАРАГАНДА 2022