Исследование структуры экспериментального сигнала с прогнозом. Лабораторная работа 4 По дисциплине Разведочная геофизика Тема " Исследование структуры экспериментального сигнала с прогнозом "
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
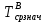 ) ) АТН – погрешность горного термометра (равна 0,5ОС) а – температурная проводимость породы верхнего слоя τ – продолжительность года (в секундах) Ниже гелиотермозоны температура не зависит от времени года и подчиняется закону Фурье. 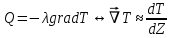 Градиент – это наиболее максимальная возможная скорость изменения температуры. Для вычисления градиента вводим оператор Гамильтона 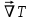 , где dT – приращение температуры кровли и подошвы породы, а dZ – мощность породы – высота между кровлей и подошвой. , где dT – приращение температуры кровли и подошвы породы, а dZ – мощность породы – высота между кровлей и подошвой. Получается температура это функция от мощности, для определения теплового потока (приближенное значение) необходимо: 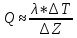 Где ∆Т – это разница температур кровли и подошвы породы, ∆Z – мощность породы. Температуру ГТЗ ( 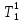 ) определяется следующим образом: из средней температуры воздуха необходимо отнять 3ОС – получится температура почвы, усреднённая. ) определяется следующим образом: из средней температуры воздуха необходимо отнять 3ОС – получится температура почвы, усреднённая. Для нахождения температуры подошвы самого верхнего слоя, а равно кровлю следующего необходимо произведение теплового потока и мощности породы разделить на теплопроводность породы и прибавить температуру гелиотермозоны. В последующих слоях эта температуру ГТЗ будет заменять температура подошвы предыдущего слоя. 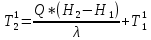 Где 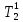 температура подошвы верхнего слоя, Н1 – высота ГТЗ, Н2 – мощность породы. температура подошвы верхнего слоя, Н1 – высота ГТЗ, Н2 – мощность породы.Следовательно, температуры подошвы верхнего слоя будет равна температуре кровли следующего слоя, а значит в расчётах не нуждается. Для вычисления температур подошв каждого слоя пород необходимо: 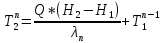 Температурная проводимость равна 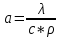 Где λ – это теплопроводность, ρ – плотность, с – теплоёмкость породы. Обозначив все данные, можно приступить к определению зоны промерзания гелиотермозоны (ГТЗ) 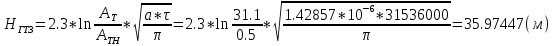 Где: АТ – амплитуда температур, разность максимальной температуры ( 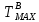 ) воздуха и среднегодовой температуры ( ) воздуха и среднегодовой температуры (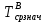 ) 14,5ОС-(-16,6ОС)=31,1ОС ) 14,5ОС-(-16,6ОС)=31,1ОСАТН – погрешность горного термометра (равна 0,5ОС) а – температурная проводимость породы верхнего слоя (гранит – 1,42857*10-6) τ – продолжительность года (в секундах) Для нахождения температуры подошвы самого верхнего слоя, а равно кровлю следующего необходимо произведение теплового потока и мощности породы разделить на теплопроводность породы и прибавить температуру гелиотермозоны. В последующих слоях эта температуру ГТЗ будет заменять температура подошвы предыдущего слоя. 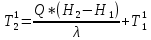 Где 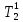 температура подошвы верхнего слоя, Н1 – высота ГТЗ, Н2 – мощность породы. температура подошвы верхнего слоя, Н1 – высота ГТЗ, Н2 – мощность породы.Следовательно, температуры подошвы верхнего слоя будет равна температуре кровли следующего слоя, а значит в расчётах не нуждается. Для вычисления температур подошв каждого слоя пород необходимо: 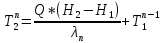 Где n – порядок слоя. Итого получились следующие данные (таблица 3) Таблица 3. Температура подошв горных пород г Оймякон
По данным можно построить геотермический разрез (рисунок 5.1–5.2). 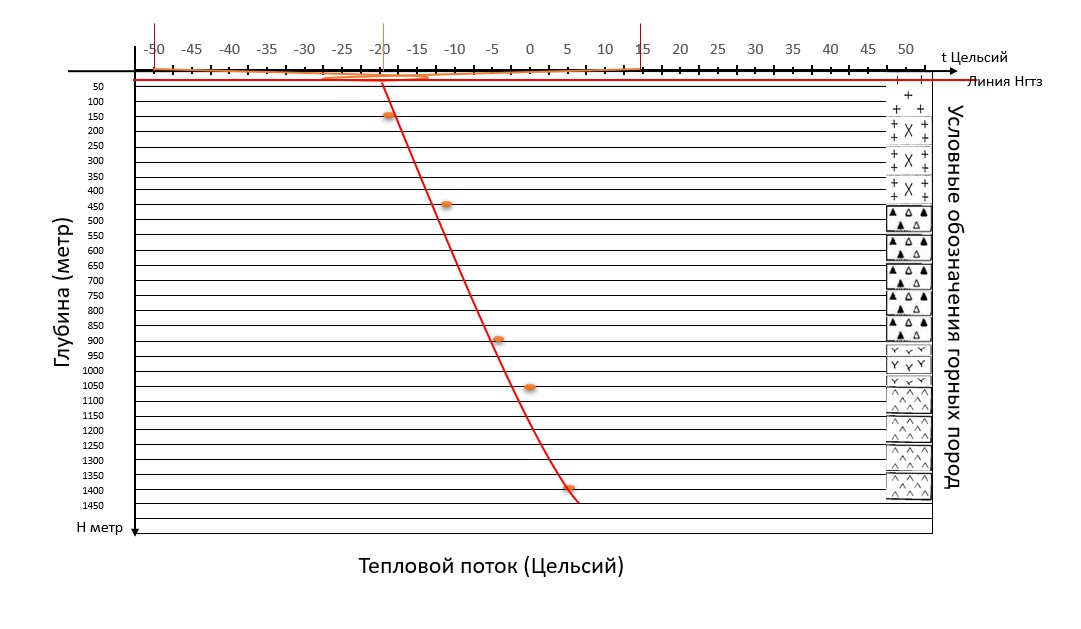 Рисунок 5.1. Построение геотермического разреза г Оймякон. Вертикальный масштаб 1:10000, по ординате глубина залегания пород (в метрах) и условное обозначение горных пород, по абсциссе температура в Цельсиях (от минимальной до максимальной среднегодовой) 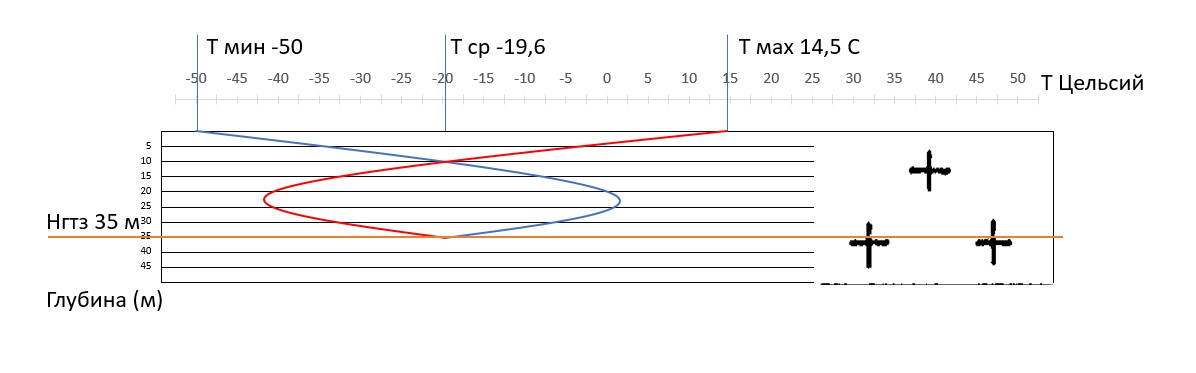 Рисунок 5.2. Построение геотермического разреза г Оймякон. Увеличен горизонтальный масштаб. Изменение температуры горной породы, в зависимости от температуры воздуха выше подошвы гелиотермозоны (Нгтз). Анализ полученных моделей Первая модель (см «Методика решения задач» страницы 11–13) представляет собой задачу, смоделированной в однородной среде. В конкретном случае однородная среда являла собой озеро, наполненное водой, возможно пресной. Для составления модели и её анализа не было предоставлено никаких точных данных, кроме выполняемого условия. Это постоянная инвазия токсичной соли в водоём. Эта концентрация увеличивалась бы по экспоненциальному тренду от минимального значения (запуск производства) до бесконечности. Однако имеется проточный ручей. С учётом того, что количество приточной ручьём воды равно воде, вытекающей из него, можно сделать следующее заключение. Озеро представлено некой чашей, наполненной до краёв. Когда с одной из сторон начинает прибывать вода, с другого, геометрически обоснованного, вытекает такое же количество воды. Эта система постоянно фильтрует воду, не давая раствору токсичной соли скапливаться в водоёме. Тогда уровень концентрации токсичной соли на графике будет представлен некой прямой линией, где изменения концентрации (по оси ординат) будет равно нулю, либо стремиться к нему. С учётом засухи, дождей, ветров эта линия не будет прямой постоянно, оттого и будет выглядеть волнистой линией. (Рисунок 2 пункт 1). Но усложнение задачи требует ввести климатический фактор: в период осень-зима, ручей будет замерзать, озеро покроется коркой льда. Но концентрация соли будет нарастать с постоянной скоростью. Закономерно, что отношение чистой воды к раствору токсичной соли будет возрастать. В период весна-лето, ручей оттает и воды его наполнятся, как и таявшей водой, так и первоначальной источной. Тогда отношение соль/вода стремительно изменится в перевес чистой воде. Это цикличный процесс от лета до зимы, и на графике будет представлять собой синусоиду (Рисунок 2 пункт 3). В любом из этих случаев возможно составить прогноз поведения токсичной соли. Когда его концентрация будет возрастать, когда снижаться. Вторая модель (Реконструкция геотемпературных разрезов город Оймякон, страницы 17–20) уже содержит некоторые данные. Так нам изначально известен тип горных пород, их глубина залегания, последовательность, их плотность, теплопроводность, теплоёмкость, температурная проводимость. С помощью этих данным возможно вычислить гелиотермозону – определённая глубина толщи горной породы, температура которой зависит от температуры воздуха. В связи с этим, математическая модель изменения температуры породы с течением времени будет представлять собой угасающую синусоиду, развёрнутую вертикально, ось ординат которой гипотетически будет глубина по оси зависимости температура/глубина, с центром системы в точке средней годовой температуры. Ось ординат будет представлять температурный график, ноль которой равняется средней годовой температуре. Однако, для синусоиды холодного времени года и тёплого времени будут равно противоположны с той лишь разницей, что ордината для синусоида холодного времени года (синяя на Рисунке 5.2) будет иметь положительное значение с увеличением температуры, а синусоида теплого времени года (красная на Рисунке 5.2) будет иметь положительное значение с уменьшением температуры. Обе синусоиды угасают на глубине, определённой как подошва гелиотермозоны. Итого обе синусоиды угаснут в координатах: подошва гелиотермозоны; среднегодовая температура в 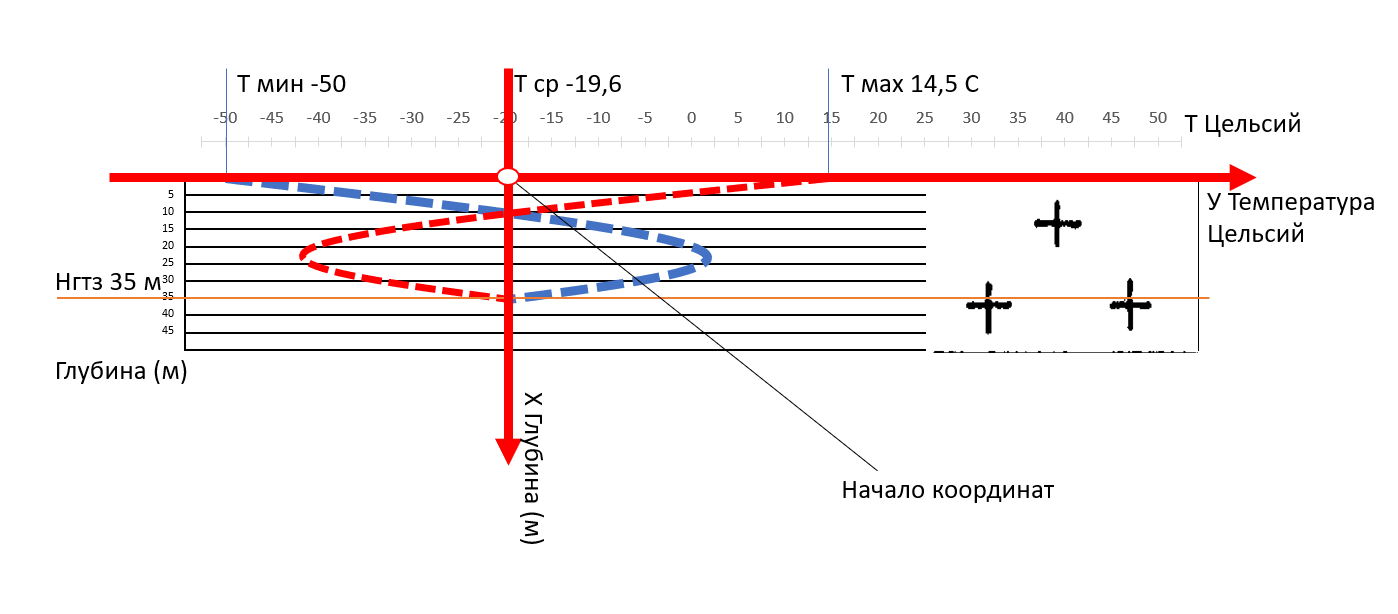 оздуха. (Рисунок 5.2). Всё вышеописанное можно рассмотреть на рисунке 6. Рисунок 6. Геотермический разрез. Представление зависимости глубины от температуры в пределах ГТЗ. Определение системы координат, представление оси абсцисс (глубина) и ординаты (температура) Средняя годовая температура обозначена за точку начала координат. Ниже подошвы гелиотермозоны, ход температуры не будет зависеть от температуры воздуха, а определяться лишь глубиной и типом горной породы. Определение температуры будет подчиняться закону Фурье. На рисунке 5.1 построен геотермический разрез, на котором можно отметить тренд, плавно увеличивающейся температуры ближе к центру Земли. Отсюда можно сделать вывод: температура неумолимо растёт с глубиной. Эта задача является неоднородной, так как имеется разнообразный состав горных пород. Задача наполнена данными, что уже отделяет её от однородной. Однако, в обеих случаях была составлена математическая модель изменения отношения по оси абсцисс и ординат; изменение представлено в виде постоянной, синусоиды и экспоненциального тренда. Обе модели связанны между собой, так как изучают изменение объекта с изменением условия. В однородной задаче изменчивость условия определяет время, в неоднородной – глубина. В той и в другой необходимо определить течение (изменение) объекта, а не сам объект. Благодаря данным в неоднородной задаче можно определить прогнозируемые точки температур кровли и подошвы горных пород. В однородной задаче математическая модель квазипериодична, так как представляет примерную модель поведения концентрации с течением времени. Какие бы данные ни были введены, получить точный прогноз в виду многих переменчивых факторов. Реально лишь определить концентрацию солей в момент времени, как и температуру на глубине в городе Оймякон, тоже возможно определить для определённой глубине, без точной прогнозировки с увеличением глубины. Исходя из этого, модели можно свести в единую модель, где по оси абсцисс изменяется условие (время/глубина), а по оси ординат моделируемый объект ( 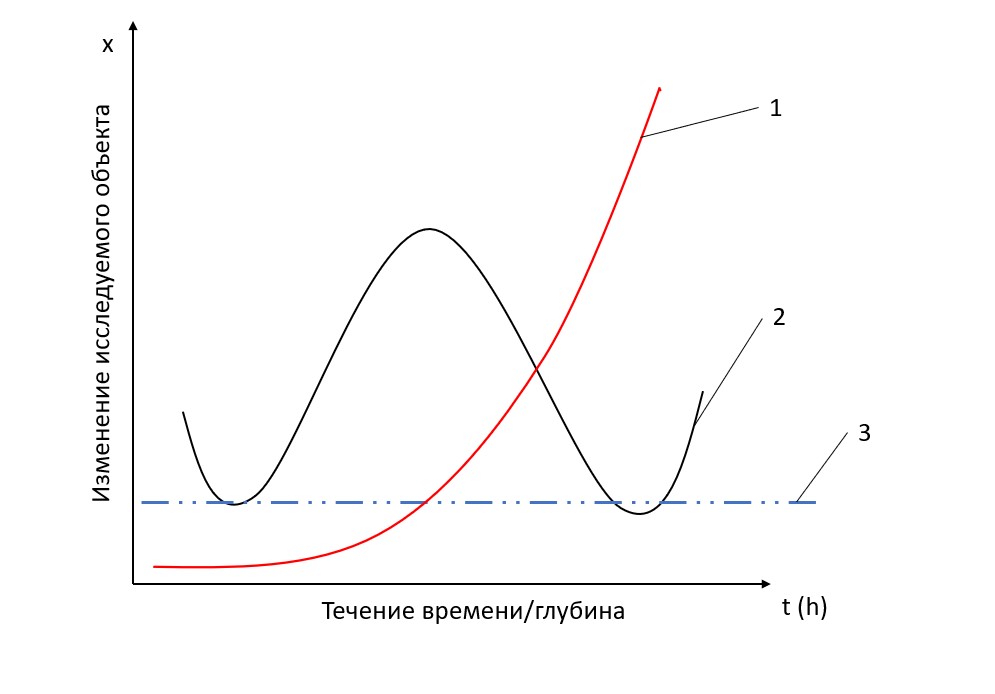 концентрация/температура). На рисунке 7 представлены эти модели. Рисунок 7. Объединение математических моделей двух задач. Абсцисса представлена изменением условий, ордината – поведение изучаемого объекта. 1 – экспоненциальный тренд увеличения температуры с увеличением глубины; 2 – синусоида изменения концентрации токсичной соли в озере с изменением сезонного климата в течение времени; 3 – постоянная концентрация при постоянном потоке ручья Заключение Подводя итоги, можно отметить следующее: 1) Однородная задача представлена квазипериодическим циклом, в котором прослеживается зависимость изменения поведения концентрации с течением времени, в разных климатических условиях. Если задача не усложняется климатическим фактором, то изменения фактически невозможно отметить, так как доподлинно неизвестно, чему равно отношение выброса токсичной соли в водоём и водоносность проточного ручья. Если это число больше или меньше единицы, тогда возможно проследить экспоненциальный тренд, в котором будет заметно увеличение или уменьшение концентрации вредных веществ. В данной модели это отношение равно 1, с небольшими погрешностями, которые могут быть вызваны различными факторами (дождь, засуха и т. д.) Задача всё же усложняется климатическими факторами, тогда прямая линия из первого условия (вернее волнистая линия с учётом погрешностей) превращается в синусоиду с квазипереодичностью, поскольку данные среднемесячной температуры могут не совпадать с действительными. Итого моделируется зависимость концентрации от времени. 2) Неоднородная задача содержит в себе уже некие данные, что помогает вывести прогноз на основе математической модели. Опять же, это условия не являются достоверными, так как в природе практически не встречается однородная горная порода. Система не учитывает различные геологические отклонения (разрывы, несогласие и т. д.). Но в любом случае прогноз по данной модели будет приблизителен и позволит определить увеличение температуры с глубиной. За исключением зоны ГТЗ определить температуру кровли и подошвы горной породы можно благодаря закону Фурье. В итоге получаем экспоненциальный тренд, зависимости температуры от глубины. На геотермальном разрезе он направлен вниз, но лишь потому, что ориентирован с условием, что начало координат по оси ординат – это линия горизонта, следовательно глубина принимает отрицательное значение. Если обозначить рост глубины как положительное значение, то линия тренда будет расти в бесконечность. Итого математическая модель – это прежде всего изменение. Съёмка данных в определённый момент даёт точные результаты, однако, исключает прогнозирование. Математическая модель – это инструмент быстрой оценки и прогноза. Благодаря этому можно увидеть полную картину и возможные последствия определённых условий. Это помогает принять оптимальное решение в кратчайшие сроки, что может спасти окружающую среду, человека, а также позволит сэкономить на проведении работ, как денежные средства, так и время, что справедливо приравнять к спасение человека. Перспективы математических моделей с минимальным значением исходных данных, или отсутствием таковых следующие: Оценка экологической катастрофы Оценка чрезвычайной ситуации, оценка зоны бедствия Оценка проведения геологоразведочных, буровых работ, маркшейдерских и т. д. Экономическая целесообразность Глоссарий Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой, а по величине равный скорости роста этой величины в этом направлении. Геохимические барьеры – это участки пространства, на которых происходит резкое уменьшение интенсивности миграции химических элементов и, как следствие, их концентрация. Петрографический анализ — метод визуального или микроскопического исследования минералогии, состава руд, шлаков, штейнов и т. д. на основании морфологических признаков. Метасоматизм - процесс замещения одних минералов другими с существенными изменениями химического состава горной породы, но с сохранением ее объема и твердогосостояния при воздействии растворов высокой химической активности; при этом происходит миграция химических элементов. Различают кремнещелочной, щелочной, кислотный и другие метасоматизмы. Гелиотермозона – внешняя зона сезонных колебаний температур. Определяется географической широтой, климатом, сезоном года, рельефом и пр. Инвариантность - свойство величин оставаться неизменными, сохраняться при тех или иных преобразованиях. Анизотропная диффузия — это итеративный процесс, в котором для вычисления каждого последующего изображения в семействе используется относительно простой набор вычислений, и этот процесс продолжается до тех пор, пока не будет получена достаточная степень сглаживания. Геотермический градиент — физическая величина, описывающая прирост температуры горных пород в «°С» на определённом участке земной толщи. Список литературы 1)Понтрягин Л. С. Дифференциальные уравнения и их приложения. -М.: Наука, 1988. - 208с. 2) Кулагин А. В., Мушин И.А., Павлова Т. Ю. Моделирование геологических процессов при интерпретации геофизических данных.-М.: Недра, 1994.-250с. 3)Петров О.В., Мовчан И.Б. Диссипативные структуры Земли и их волновая природа //Региональная геология и металлогения.-2007. №30–31. -С.12-37. 4)Ибрагимов Н. Х. Практический курс дифференциальных уравнений и математического моделирования.-М.: Физматлит,2012.-332с. 5) Костицын В. И., Хмелевской В. К. Геофизика: Перм. гос. нац. исслед. ун-т. – Пермь, 2018. – 428 с. 6) Н. Б. Дортман, А. А. Молчанов. Петрофизика: Справочник. В трех книгах. Книга вторая. Техника и методика исследований. – М.: Недра, 1992.-256 с. |
