Исследование структуры экспериментального сигнала с прогнозом. Лабораторная работа 4 По дисциплине Разведочная геофизика Тема " Исследование структуры экспериментального сигнала с прогнозом "
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский горный университет» Кафедра геофизических и геохимических методов поисков и разведки месторождений полезных ископаемых ЛАБОРАТОРНАЯ РАБОТА №4 По дисциплине: Разведочная геофизика Тема: "Исследование структуры экспериментального сигнала с прогнозом" (подпись) (Ф.И.О.) (подпись) (Ф.И.О.) Санкт-Петербург 2021 Аннотация Сегодня, чтобы получить инженерно-геологические сведения, необходимые для прогнозирования инженерно-геологической обстановки определенного земельного участка, применяется множество разнообразных технологий изысканий. На различных стадиях инженерно-геологических исследований может использоваться одновременно несколько методик анализа геологической среды. Составление формализованных моделей природно-технических систем в отсутствии фактических данных один из оптимальных способов представления всей картины требуемой ситуации. Опираясь на математические модели, можно сделать прогноз без подробной информации, то есть отсутствие съёмок, измерений, показателей и так далее в однородной среде. В неоднородной среде без минимальных данных обойтись будет гораздо сложнее, однако без подробнейшей рекогносцировки, несомненно, возможно изобразить определённый план, который требуется в настоящий момент. Всё это можно отнести к разряду ранней диагностики, когда требуется определиться с масштабом планируемых изысканий на местности, финансового расчёта, поиска лучшего способа проведения исследований, а также геологических, геодезических, геофизических работ. Нельзя не отметить также оценку чрезвычайных ситуаций, когда присутствует необходимость моментального реагирования и устранения проблемы – это может быть экологическая катастрофа, природно-стихийные бедствия; прогноз сейсмической ситуации жилой, промышленной зон, а также в труднодоступной местности для рентабельности проводимых работ и безопасности человека и окружающей среды. Одним словом, современное положение, начиная от экологии, заканчивая геополитическими и экономическими факторами заставляет человеческое общество более вдумчиво распределять ресурсы. Другими словами, без теоретической базы и модельных представлений, проведение любых работ считается необоснованным и вредит как планете, так и социуму и конкретно отдельно взятого человека. Содержание Введение Жизнь любого человека сопровождается процессами моделирования и различными моделями. Использование различных учебных пособий, макетов в школьные годы, проведение лабораторных экспериментов, расчетов в студенческие годы, разработка чертежей, проектирование и расчет реальных устройств и процессов, построение теорий различного рода и назначения – примеры использования моделей и моделирования, когда реальные объекты и процессы заменяются их отображениями (моделями, описаниями и т. д.). Если кратко охарактеризовать моделирование, то оно заключается в замене реальной системы (процесса, явления) моделью, которая находится с ней (с ними) в некотором соответствии и способна воспроизводить интересующие исследователя свойства или характеристики реальной системы. Безусловно, моделирование является не единственным методом изучения окружающего нас мира. Но роль моделирования в науке, в исследованиях инженерных, организационных, экономических объектов и систем и, вообще, в жизни человека, весьма велика. Можно утверждать: познание любого объекта, системы, процесса, явления сводится, по существу, к созданию его (ее) модели. Познание и изучение окружающего нас мира можно осуществлять различными способами и методами. Но при исследовании различных сложных объектов, явлений, процессов, при создании, организации и оптимизации сложных систем метод моделирования является одним из самых мощных методов. Так, перед изготовлением любого технического устройства или сооружения разрабатывается его модель-проект, человек, прежде чем совершить что-либо, обдумывает возможную последовательность действий и возможные последствия этих действий, организуя взаимодействие множества объектов, т.е. организуя деятельность некоторой системы, человек организует систему так, чтобы получить максимальный эффект от деятельности такой системы и т.д. Причиной все более расширяющегося применения моделей является то, что процессы, происходящие в модели, можно регистрировать, проверять их соответствие результатам теоретического анализа, заменять аналитические расчеты процессов их непосредственным наблюдением, т. е. эффективно решать все основные задачи экспериментального исследования. Что такое модель? Это предельные упрощение исследования природных систем с целью их формального описания. Тогда как математическое моделирование – это знаковое моделирование, при котором описание объекта осуществляется на языке математики, а исследования модели проводятся с использованием тех или иных математических методов. В настоящее время это один из самых результативных и наиболее часто применяемых методов научного познания. Преимуществами математического моделирования по сравнению с другими видами моделирования являются: - экономичность, сбережение ресурсов реальной системы; - возможность моделирования гипотетических, т. е. нереализованных в природе объектов и систем; - возможность реализации режимов, опасных или трудновоспроизводимых в реальности; - возможность изменения масштаба времени; - универсальность технического и программного обеспечения, наличие пакетов прикладных программ для проведения широкого круга работ; - возможности прогнозирования и выявления общих закономерностей; - возможности сравнительно простого многофакторного анализа. В качестве примеров математического моделирования в различных областях человеческой деятельности можно указать расчет траекторий космических аппаратов, прогнозирование погодных явлений, расчет и проектирование машин и устройств любой сложности, моделирование процессов в экономике, использование математических моделей в медицине, биологии и многое другое. В геофизике формализованные модели природно-технических систем, возможные без фактических данных включают в себя следующие задачи: 1. Основываясь на математических моделях получить представление о геофизических данных исследуемого объекта. 2. Производить анализ объектов находящихся вне досягаемости прямых измерений с примерными прогнозами поведения среды (актуально при ЧП). 3. Выявление поведения объекта и его влияния на внешнюю среду на долгосрочную перспективу. 4. Оптимизация ввода и обработки массивов данных об объектах изыскания. Применение обыкновенных дифференцированных уравнений (ОДУ) в описании динамики и в прогнозе горных систем. Постановка аналитического моделирования характеризует то, что процессы функционирования системы записываются в виде некоторых функциональных соотношений (алгебраических, дифференциальных, интегральных уравнений). При моделировании основываясь на анализе возможных данных удается получить только для сравнительно простых систем. Для сложных систем часто возникают большие математические проблемы. Для применения аналитического метода идут на существенное упрощение первоначальной модели. Однако исследование на упрощенной модели помогает получить лишь ориентировочные результаты. Аналитические модели математически верно отражают связь между входными и выходными переменными и параметрами. Но их структура не отражает внутреннюю структуру объекта. Конечно, нахождение решений при таком моделировании оказывается исключительно ценным для выявления общих теоретических закономерностей простых линейных цепей, систем и устройств. Но его сложность резко возрастает по мере усложнения воздействий на модель и увеличения порядка и числа уравнений состояния, описывающих моделируемый объект. Разнообразие математических моделей, используемых в науках о Земле, делает невозможным их анализ или даже просто обзор. Так, например, математическое моделирование гравитационных и магнитных полей составляет значительную часть гравиметрии и магнитометрии. Моделирование свойств среды по результатам измерения гравитационных и магнитных полей составляет значительную часть теории интерпретации данных магниторазведки и гравиразведки. То же самое можно сказать о волновых сейсмических полях, полях температур, фильтрации и движения нефти в пласте в процессе эксплуатации нефтяных и газовых месторождений и многого другого. Поэтому целью и задачей настоящей работы служат внесение ясности в принципиальные вопросы построения математических моделей в некоторых распространённых разделах наук о Земле. При многообразии задач, возникающих при моделировании в науках о Земле, можно выделить три их класса, которые называются первой, второй и третьей задачами моделирования: 1) моделирование следствий из принятых моделей среды и моделей процессов, управляющих изучаемыми следствиями; 2) моделирование среды – создание моделей среды по известным следствиям и моделям процессов, управляющих наблюдаемыми следствиями; 3) моделирование процессов по известным моделям среды и наблюдаемым следствиям этих процессов. Также стоит упомянуть о трех главных составляющих математической модели: Предельное упрощение геометрии объекта; Граничные начальные условия; ДУ описывающее, случайный процесс Геофизические математические задачи - задачи, возникающие при анализе физических явлений, изучаемых в связи с исследованиями строения Земли. В зависимости от природы изучаемых физических явлений различают следующие виды геофизических исследований: гравиразведку, основанную на изучении гравитационного поля; магниторазведку, основанную на изучении постоянного магнитного поля; сейсморазведку, основанную на изучении распространения упругих колебаний: электроразведку, основанную на изучении электрического поля постоянного тока или переменного электромагнитного поля; радиометрию, основанную на измерении интенсивности излучения естественной или вызванной радиоактивности горных пород. Измерение полей может производиться на поверхности Земли (наземные методы), в воздухе (аэроразведка) и в скважинах (каротаж скважин). Математические задачи, возникающие в гравиразведке и в магниторазведке, схожи. В обоих случаях прямая задача сводится к решению уравнения Пуассона или неоднородного уравнения Лапласа в близи источника: 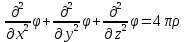 , где φ – потенциал физического поля, ρ – объемная плотность физического поля. , где φ – потенциал физического поля, ρ – объемная плотность физического поля.Или 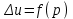 - неоднородное уравнение Лапласа – уравнение Пуассона. - неоднородное уравнение Лапласа – уравнение Пуассона.Уравнение вида: 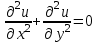 или или 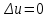 - называется уравнением Лапласа. - называется уравнением Лапласа. Оно описывает стационарный процесс с установившимся распределением температуры сплошной среды. Описывает любые установившиеся процессы. При наличии источников тепла получаем уравнение: 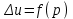 - неоднородное уравнение Лапласа – уравнение Пуассона. - неоднородное уравнение Лапласа – уравнение Пуассона.Природный процесс существования магнитного и электрического полей основан на системе уравнений Максвелла, которые являются основополагающими для магниторазведки: 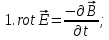 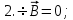 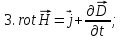 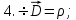 Из вышеприведённых уравнений Максвелла следует: 1) Электрическое и магнитное поля взаимосвязаны, т. е. в общем случае электрическое и магнитное поля не могут существовать независимо друг от друга. Следовательно, существует единое электромагнитное поле. 2) Уравнения Максвелла являются инвариантными относительно преобразований Лоренца, т. е. их вид не меняется при переходе от одной ИСО к другой. А также подтверждающий, что магнитных зарядов в природе не существует, магнитное поле не имеет стоков и истоков, то есть является замкнутым. 3) Уравнение показывает, что магнитные поля могу порождаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями. 4) Постулат Максвелла, выражающий закон создания электрических полей действием зарядов в произвольных средах. Если рассматривать основополагающие физические законы в сейсморазведке, то сразу же вспоминаются законы оптики, а именно распространение акустической волны в однородной среде, то ее движение в общем случае описывают волновым уравнением (дифференциальным уравнением в частных производных). Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым. 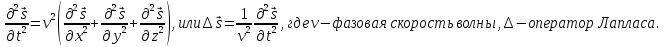 Применение данного уравнения распространяется в описании электромагнитной волны, задача малых поперечных колебаний струн, а также в описании колебательных процессов в акустических средах. Нахождение применения данного уравнения для описания гравитационных волн. Уравнение диффузии представляет собой частный вид дифференциального уравнения в частных производных. Бывает нестационарным и стационарным. В смысле интерпретации при решении уравнения диффузии речь идет о нахождении зависимости концентрации вещества (или иных объектов) от пространственных координат и времени, причем задан коэффициент (в общем случае также зависящий от пространственных координат и времени), характеризующий проницаемость среды для диффузии. При решении уравнения теплопроводности речь идет о нахождении зависимости температуры среды от пространственных координат и времени, причем задана теплоёмкость и теплопроводность среды (также в общем случае неоднородной). В общем виде уравнение диффузии записывается следующим образом: 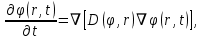 где φ(r, t) — плотность диффундирующего вещества в точке r и во время t и D(φ, r) — обобщённый коэффициент диффузии для плотности φ в точке r; ∇ — оператор набла. Если коэффициент диффузии зависит от плотности — уравнение нелинейно, в противном случае — линейно. Если D — симметричный положительно определённый оператор, уравнение описывает анизотропную диффузию: 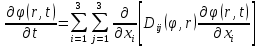 Если D постоянное, то уравнение сводится к уравнению теплопроводности: 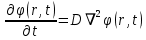 Решением уравнения диффузии будет выглядеть следующим образом: Для одномерного случая: 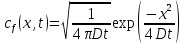 В случае произвольного начального распределения c(x, 0) общее решение уравнения диффузии представляется в интегральном виде как свёртка: 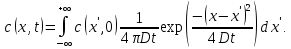 В стационарном случае уравнение диффузии сводится к решению уравнения Пуассона (неоднородное) или Лапласа (при f = 0): 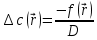 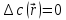 Уравнение неразрывности в дифференциальной форме В потоках несжимаемой жидкости, в которых нет ни оттока, ни присоединения расхода, объемный расход в любом сечении постоянный. Можно поэтому предположить, что в каждой точке внутри потока должно выполняться соотношение, гарантирующее, что в ней не происходит ни исчезновения, ни возникновения жидкости. Таким уравнением является уравнение неразрывности в дифференциальной форме. Если поток в каждой точке задан вектором скорости U (x, y, z), то уравнение неразрывности будет выглядеть следующим образом: 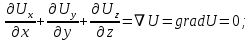 Уравнение неразрывности должно выполняться в каждой точке потока жидкости. Решение уравнения неразрывности сводится к нахождению частных производных по трем координатам от функции трех переменных, затем находится сумма этих трех составляющих. Если полученный результат равен нулю, то справедливо судить о том, что условие неразрывности выполняется и потом жидкости может существовать. Для аналитического моделирования характерно, что процессы функционирования системы записываются в виде некоторых функциональных соотношений (алгебраических, дифференциальных, интегральных уравнений). Аналитическая модель может быть исследована следующими методами: 1) аналитическим, когда стремятся получить в общем виде явные зависимости для характеристик систем; 2) численным, когда не удается найти решение уравнений в общем виде и их решают для конкретных начальных данных; 3) качественным, когда при отсутствии решения находят некоторые его свойства. Аналитические модели удается получить только для сравнительно простых систем. Для сложных систем часто возникают большие математические проблемы. Для применения аналитического метода идут на существенное упрощение первоначальной модели. Однако исследование на упрощенной модели помогает получить лишь ориентировочные результаты. Аналитические модели математически верно отражают связь между входными и выходными переменными и параметрами. Но их структура не отражает внутреннюю структуру объекта. Например, подключив RC –цепь к источнику постоянного напряжения ε, можно составить аналитическое выражение для временной зависимости напряжения u(t) на конденсаторе C: 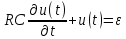 Это линейное дифференциальное уравнение (ДУ) и является аналитической моделью данной простой линейной цепи. Его аналитическое решение, при начальном условии u(0) = 0, означающем разряженный конденсатор в момент начала моделирования, позволяет найти искомую зависимость – в виде формулы: 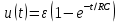 Однородные и неоднородные модели и их применимость в горном деле. Эффективность вероятностно-статистического подхода при решении задач разведочной геофизики во многом определяется уровнем используемых при этом модельных представлений. Статистические методы ориентированы в основном на математические модели, характеризующие внешние признаки исследуемого объекта, что, в частности, типично для задач статистического оценивания. распознавания и аппроксимации. В значительно меньшей степени распространено использование стохастических (вероятностных) моделей, задающих описание внутреннего строения объекта исследования, хотя именно такие модели позволяют устанавливать особенности проявления его структуры во внешних признаках, например, в физических полях. Стохастическое моделирование основывается на представлении о множестве, возможно, бесконечном, случайных состояний модели объекта. Такое множество может быть охарактеризовано относительно небольшим числом параметров вероятностных распределений случайных характеристик модели. Вероятностное описание определяет высокую степень параметризации, а, следовательно, и устойчивость стохастических моделей. Построение таких моделей во многом опирается на информацию, получаемую при формировании детерминированных или статистических физико-геологических моделей. Потенциальная область применения стохастических моделей при планировании геофизических экспериментов в анализе данных достаточно обширна, так как во многих случаях они позволяют получать весьма строгие решения задач, формализация которых в рамках детерминированного подхода или эмпирической статистики крайне затруднена или вообще невозможна. Описание неоднородных геологических объектов Существенной чертой реальных геологических тел является неоднородность их строения, которая в качественном отношении обычно отражается в описаниях структуры месторождений полезных ископаемых или в классификации пород и руд по их текстурно-структурным признакам. Естественно, что количественные оценки влияния неоднородности объекта на его свойства возможны только на основе построения его математической модели. Многообразие возможных реализаций строения минерального вещества, обладающего одной и той же текстурно-структурной характеристикой, практическая невозможность задания огромного числа параметров для описания положения, геометрии и физических свойств каждой неоднородности определяют целесообразность привлечения стохастических моделей для описания сложных ситуаций. Основное преимущество таких моделей – относительно небольшое число параметров, достаточных для описания характеристик и особенностей неоднородных сред. Это свойство стохастических моделей принципиально, поскольку их параметры содержат вероятностную информацию обо всех возможных состояниях моделируемого объекта. Большинство рассматриваемых моделей в той или иной степени идеализируют реальные объекты, но даже ограниченное число предлагаемых стохастических моделей удовлетворительно аппроксимирует достаточно большое число возможных ситуаций. Примерами таких случаев могут служить модели случайных сред, объекты с неоднородным строением и др. Представленное выше описание неоднородных геологических объектов и соответствующие стохастические модели определяют (в вероятностном смысле) физические свойства или содержания химических элементов в любой точке объекта. Во многих случаях такие «точечные» характеристики не соответствуют реальным условиям эксперимента, осуществляемого физическим устройством, всегда определяющим с той или иной разрешающей способностью эффективное (интегральное, суммарное) значение свойства для некоторой части объёма объекта. Аналогичные ситуации возникают и при вычислении обобщённых физических свойств структурно-вещественных комплексов, составляющих основу петрофизических моделей, при геохимическом и геологическом опробовании неоднородных сред Методика решения задачи Н  а берегу озера, объёмом V литров, расположено промышленное предприятие, выделяющее в водоём некоторое количество токсичной соли, которая равномерно распределена по всему водоёму в виде водного раствора (Рисунок 1). Концентрация токсичной соли изменятся благодаря проточному ручью, приносящий v литров чистой воды и забирающий на другом конце озера ровно такое же количество воды. Предположим, что величина поступление в водоём раствора токсичной соли от предприятия величина постоянная и не изменяется с ходом течения времени. Превосходит ли водоизмещение ручья постоянную поступления соли в водоём доподлинно неизвестно, как и сезонность протока. Рисунок 1. Эскиз системы условия задачи: 1 – Предприятие, выпускающее в водоём (2) токсичную соль (поток обозначен черной стрелкой (4)); 2 – озеро, имеющее проточный ручей (поток обозначен синей стрелкой (3)); 3 – движение проточного ручья; 4 – выпуск токсичной соли. Предположим, что предприятие выделяет постоянное количество токсичной соли, которое изменяется незначительно – это многообразные факторы, которые могут изменять концентрацию соли в водоёме (например засуха, обильные осадки, остановки производства и т. д.) Поэтому на графике (Рисунок 2), линией 1 обозначена кривая, которая предполагает погрешности, но в упрощённой модели принято считать её прямой линией, параллельной абсциссе – оси, указывающее на течение времени.  При усложнении задачи вводится климатический фактор: в сентябре температура начинает опускаться ниже отметки 0ОС, следовательно объём проточного ручья начинает уменьшаться, в октябре объём настолько незначителен, что концентрация начинает резко увеличиваться. С ноября ручей замерзает, следовательно, содержание токсичной соли будет увеличиваться с большей скоростью. Начиная с марта, концентрация замедляет рост и начинает падение. Весной, когда скопившиеся осадками снега начинают таять, водоток резко увеличивается, поэтому происходит резкое снижение концентрации солей в озере. Для построения графика необходимо построить точки, в которых смоделированы среднемесячная концентрация выбросов предприятия. Для этого, предположим, что концентрация в августе минимальна, а в январе – максимальна. Обозначим концентрацию в августе за х, тогда концентрация в январе 6х. Содержание опасных веществ с августа по январь будет 1 Рисунок 2. Построение графической модели изменения концентрации токсичной соли в водоёме с течением времени. 1 – изменение концентрации, при постоянном сохранении условия проточности озера; 2 – график среднемесячного количества концентрации соли; 3 – изменение концентрации при усложнении задачи. Для вычисления определённой формулы предположим, что в определённый момент времени t, в озере равномерно распределено x килограммов токсичной соли, значит, в каждом литре раствора её концентрация составляет  кг/л, где a – объём озера в литрах. Тогда при разбавлении проточным водотоком втекает и вытекает b литров воды. Следовательно, концентрация разбавления будет составлять кг/л, где a – объём озера в литрах. Тогда при разбавлении проточным водотоком втекает и вытекает b литров воды. Следовательно, концентрация разбавления будет составлять  кг/л. кг/л. Так как разбавление связано с уменьшением концентрации соли в воде, то скорость изменения концентрации будет равна обратному значению разбавления 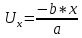 Скорость – это изменение количества вещества x за определённое количество времени t, что можно выразить как 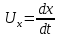 , где dx – это изменение количество вещества, а dt – течение времени. Это значит, чтобы выразить изменение количества концентрации токсичной соли в водоёме с течением времени, необходимо скорость изменения концентрации выразить как отношения dx/dt. В итоге мы получаем закон, по которому изменяется содержание вредных солей в воде: , где dx – это изменение количество вещества, а dt – течение времени. Это значит, чтобы выразить изменение количества концентрации токсичной соли в водоёме с течением времени, необходимо скорость изменения концентрации выразить как отношения dx/dt. В итоге мы получаем закон, по которому изменяется содержание вредных солей в воде: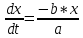 Предположим, что озеро – это чаша, с постоянным объёмом, который обозначен как «a». Тогда проточный ручей переполняет эту чашу с одной стороны, выливая тот же объём из переполненной чаши с другой стороны. Усложнение задачи вызвано погодными изменениями, когда проток полностью замерзает. Следовательно объём озера перестанет увеличиваться на величину b литров. Значит объём озера a=const. Тогда в зимний сезон, концентрация токсичных солей будет протекать по следующему закону: 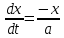 Перенесём величину x влево, а величину dt вправо, для составления уравнения: 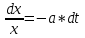 Выполним интегрирования для определения константы, где С – постоянная интегрирования. 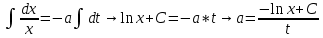 Природа собственного теплового излучения Нагретые объекты излучают энергию не только в инфракрасном, но и в радиодиапазоне, хотя радиотепловое излучение по интенсивности значительно уступает инфракрасному. Радиотепловое излучение формируется определённым излучательным слоем, так называемым скин-слоем. Мощность этого слоя тем больше, чем длиннее волна излучения. Основным показателем радиотеплового излучения является радиояркостная (Радиояркостная температура системы атмосфера–поверхность на частоте ν под углом θ, регистрируемая антенной радиометра на искусственном спутнике Земли определяется следующим выражением: 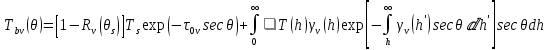 + +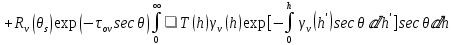 , где , где 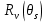 – энергетический коэффициент отражения поверхности, – угол падения излучения на подстилающую поверхность, – энергетический коэффициент отражения поверхности, – угол падения излучения на подстилающую поверхность, 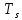 – температура поверхности, – интегральное зенитное поглощение радиоволн в зените, – температура поверхности, – интегральное зенитное поглощение радиоволн в зените,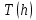 – вертикальный профиль температуры, – вертикальный профиль температуры, 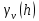 – погонный коэффициент поглощения. ) температура Тя, измеряемая в К˚ - произведение абсолютной температуры Т t и коэффициента излучения æ (закон Релея-Джинса). Тя= æ Т t – погонный коэффициент поглощения. ) температура Тя, измеряемая в К˚ - произведение абсолютной температуры Т t и коэффициента излучения æ (закон Релея-Джинса). Тя= æ Т tОсновной приток энергии к Земле обеспечивается солнечным излучением и составляет около 341 Вт/м² в среднем по всей поверхности планеты. Внутренние источники тепла (радиоактивный распад, стратификация по плотности) по сравнению с этой цифрой незначительны (около 0,08 Вт/м²). Из 341 Вт/м² солнечного излучения, попадающего на Землю, примерно 30 % (102 Вт/м²) сразу же отражается от поверхности Земли (23 Вт/м²) и облаков (79 Вт/м²), а 239 Вт/м² в сумме поглощается атмосферой (78 Вт/м²) и поверхностью Земли (161 Вт/м²). Поглощение в атмосфере обусловлено, в основном, облаками и аэрозолями. Из 161 Вт/м² поглощаемой поверхностью Земли энергии 40 Вт/м² возвращается в космическое пространство в виде теплового излучения диапазона 3–45 мкм, ещё 97 Вт/м² передаются атмосфере за счёт различных тепловых процессов (80 Вт/м² — испарение воды, 17 Вт/м² — конвективный теплообмен). Кроме того, около 356 Вт/м² излучения Земли поглощается атмосферой, из которых 332 Вт/м² (161–40–97–356 + 332 = 0) возвращается в виде обратного излучения атмосферы. Таким образом, полное тепловое излучение поверхности Земли составляет 396 Вт/м² (356+40), что соответствует средней тепловой температуре 288 К (15 °С). Атмосфера излучает в космическое пространство 199 Вт/м², включая 78 Вт/м², полученные от излучения Солнца, 97 Вт/м², полученные от поверхности Земли, и разность между поглощаемым атмосферой излучением поверхности и обратным излучением атмосферы в объёме 23 Вт/м² Землю солнечного излучения совпадает с энергиейобратного теплового излучения Земли. Это означает, что каждый фотон солнечного излучения (частица света - световой квант) распадается в среднем на Т / Г, 6000 / 30020 фотонов теплового излучения, которые рассеиваются Землей обратно в космическое пространство. В результате такого стабильного энергетического баланса на земной поверхности сохраняется постоянная средняя температура, равная 15 С. Такая температура способствует нахождению воды в жидком состоянии, что обеспечивает использование ее в жизненных процессах. На ближайших от Земли планетах солнечной системы эта температура весьма далека от оптимальной: на Венере - плюс 477 С, на Марсе - минус 53 С. Такое различие температур объясняется разными значениями солнечной постоянной на этих планетах из-за их различной удаленности от Солнца: Венера - на 108 1 млн. км, Земля - на 149 5 млн. км, Марс - на 227 8 млн. км. Тропосфера почти не задерживает идущую к Земле коротковолновую солнечную радиацию, зато поглощаеттепловое излучение Земли и нагревается, вследствие чего образуются облака и выпадают осадки. Углекислый газ обладает тепличным (парниковым) эффектом: он свободно пропускает солнечные лучи и задерживаетотраженное тепловое излучение Земли. Солнце излучает огромное количество теплоты на Землю, годовое его значение примерно в 10 раз больше всей тепловой энергии, которая заключена во всех разведанных запасах органического топлива планеты. Однако количество усвояемой Землей солнечной энергии ничтожно мало. Эффект тепличный - эффект, обусловленный нагреванием внутренних слоев атмосферы Земли вследствие прозрачности атмосферы для основной части излучения Солнца и поглощения ею основной инфракрасной части |
