Лр по физике. Лр_41_2_Определение радиуса кривизны линзы интерференционным мет. Лабораторная работа 41 2

• Название: Лабораторная работа 41 2
• Анкор: Лр по физике
• Дата: 13.09.2022
• Размер: 369.57 Kb.
• Имя файла: Лр_41_2_Определение радиуса кривизны линзы интерференционным мет.docx
• Тип: Лабораторная работа; #675515

Лабораторная работа 41₂

Определение радиуса кривизны линзы интерференционным методом

Цель работы: изучение интерференции в тонких плёнках на примере колец Ньютона и определение радиуса кривизны линзы.

Теоретическое введение

Две волны одинаковой частоты и одного направления колебаний A₁=A₁₀cos(ωt+α₁) и A₂=A₂₀cos(ωt+α₂), накладываясь друг на друга, в данной точке пространства возбуждают результирующее колебание, амплитуда которого определяется выражением

А²=А ₁²+А₂²+2 А₁ A₂ cosδ .

Если разность фаз δ=α₁ - α₂ остаётся постоянной во времени и в пространстве, то волны являются когерентными. Поскольку в однородной среде интенсивность волны пропорциональна квадрату её амплитуды (I=А²), то для когерентных волн интенсивность результирующей волны равна:

I = I₁ +I₂ +2(I₁I₂)^0.5cosδ.

Явление взаимного усиления (cosδ >0) или ослабления (cosδ <0) двух (или большего числа) волн при их наложении друг на друга называется интерференцией. Перераспределение светового потока в пространстве приводит к возникновению в одних местах пространства максимумов, а в других - минимумов интенсивности. Если интенсивность двух интерферирующих волн одинакова, в максимумах I=4I₁, в минимумах I=0. В случае некогерентных волн разность фаз δ непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение cosδ=0. Интенсивность результирующей волны одинакова и равна I = I₁+I₂ (или I = 2I₁).

Естественные источники света не когерентны, так как излучение слагается из волн, испускаемых многими атомами в течение короткого времени (10 ^-8с); фазы волн не связаны друг с другом, и фаза результирующей волны претерпевает случайные изменения.

Когерентные световые волны можно получить, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником, на две части. Если эти две волны, пройдя разные оптические пути, приобретут разность хода, сравнимую с длиной волны, а затем наложатся друг на друга, будет наблюдаться интерференция.

В данной работе изучается интерференция двух световых волн: I) - волны, отраженной от границы тонкой воздушной прослойки с выпуклой сферической поверхностью линзы и 2) - волны, отраженной от границы воздушной прослойки с плоской поверхностью соприкасающейся с линзой стеклянной пластинки (рис.1).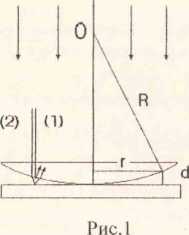



Интерферируют лучи, близкие к аксиальным, для которых г << R.

Пусть сверху на плоскую поверхность линзы нормально к ней падает монохроматический параллельный пучок света. При вычислении разности хода можно пренебречь небольшими наклонами лучей в тонком воздушном зазоре. Геометрическая разность хода между интерферирующими лучами равна 2d, где d - толщина воздушного зазора в данном месте.

При вычислении оптической разности хода нужно учесть изменение фазы световой волны при отражении от границ стекло-воздух и воздух-стекло. Для светового (электрического) вектора отражение от оптически более плотной среды происходит с изменением фазы на π. Свет, отраженный от границы стекло-воздух, по сравнению со светом, отраженным от границы воздух-стекло, приобретает, таким образом, дополнительный фазовый сдвиг на π, что соответствует разности хода λ/2. Оптическая разность хода А равна

А = 2d + λ/2.

Линии одинаковой разности хода представляют собой концентрические кольца с центром в точке соприкосновения сферической поверхности линзы с плоской поверхностью стеклянной пластинки. Эти кольца называются кольцами Ньютона. При определённом значении длины волны λ разность хода А определяется толщиной воздушного зазора, которая одинакова вдоль линии окружности каждого кольца. Интерференционные линии являются, таким образом, «полосами равной толщины».

Условия тёмных и светлых полос соответствуют условиям наблюдения минимума и максимума интерференции:

min: 2d + λ/2 = (2m+1 )·λ/2 m=0,l ,2,... (1)

max: 2d + λ/2 = 2m·λ/2 m=0,l ,2,... (2)

В соответствии с рис.1 радиусы колец Ньютона (г) связаны с толщиной воздушного зазора (d) и радиусом кривизны линзы (R):

г² = R² + (R - d)²= 2Rd - d².

Принимая во внимание, что 2R >> d, получим

r² = 2Rd (3)

Из (1), (2) и (3) получим выражения для радиусов тёмных или светлых колец r_m^гемн=(mRλ)^0.5,

r_m^светл= ((2m + 1)Rλ/2)^0.5 (4)

Измеряя радиусы различных интерференционных колец в монохроматическом отраженном свете с известной длиной волны, можно определить радиус кривизны (R) сферической поверхности линзы.

Описание установки

• 
  Установка состоит из микроскопа, закрепленного на основании со стойкой, линзы с пластиной и комплекта светофильтров (Рис.2).
  
• 
  В микроскопе установлен окуляр 8х с измерительной шкалой.
  
• 
  Линза с пластиной представляет собой оправу, в которую помещены стекляная пластинка и соприкасающаяся с ней линза большого радиуса. Устройство предназначено для изучения интерференционной картины "колец Ньютона".
  
• 
  Насадка для микроскопа представляет собой трубку с разрезом и резьбой, позволяющую крепить её на место одного из окуляров. Внутренний диаметр насадки предусматривает возможность установки интерференционных светофильтров и крепления осветителя микроскопа.
  
• 
  Комплект светофильтров состоит из 4 интерференционных светофильтров в оправе, которая позволяет вставлять их в насадку для микроскопа, и которые используются для вырезания определенной длины волны из излучения лампы осветителя при измерении диаметров колец Ньютона.
  

В установке используются светофильтры с длинами волн (нм):

435 ±10; 546 ±10; 578 ±10; 630 ±10

Рис.2. 1- светофильтры; 2- линза с пластинкой; 3- осветитель; 4 - насадка для микроскопа; 5- окуляр микроскопа со шкалой; 6 – переключатель увеличения объектива микроскопа.	Рис. 3. Вид интерференционной картины.

Порядок выполнения работы

1. 
   Установите на предметный столик микроскопа линзу с пластинкой в оправе 2 (рис. 2).
   

2. 
   Переключите увеличение объектива микроскопа на 0,6^х и передвигая линзу с пластинкой, отъюстируйте микроскоп до появления в окуляре микроскопа интерференционной картины колец Ньютона.
   

3. 
   Постепенно меняя увеличение объектива микроскопа в сторону увеличения отъюстируйте микроскоп до заполнения интерференционными кольцами всего поля окуляра (см. рис. 3). Прямая линия измерительной линейки окуляра микроскопа должна проходить через центр интерференционной картины.
   

4. 
   Измерьте диаметры тёмных колец.
   

Для этого визуально зафиксируйте положение достаточно удаленного от центра, но еще отчетливо видимого темного кольца. По шкале окуляра микроскопа определите положение данного темного кольца слева от центра интерференционной картины, занесите это значение в Таблицу 1. Далее фиксируйте положение темных колец следующего, меньшего диаметра и записывайте соответствующие показания в Таблице 1 (в соответствии с номером кольца). После прохождения через центральное пятно продолжайте измерения, записывая возрастающие номера колец и координаты их положений.

5. 
   Рассчитайте радиус колец, используя паспортные данные установки. Таблица 1
   

Номер кольца	Отсчет по шкале окуляра микроскопа		Диаметр кольца, дел	Радиус кольца, дел	Радиус кольца, мм
	Слева от центра	Справа от центра
7
6
5
4
3
2
1

6. 
   Определите радиус кривизны линзы.
   

Согласно формуле (4) для тёмных колец с номерами m и к имеем:

г_m² = mRλ и г_к² = kRλ , откуда получаем формулу для радиуса кривизны линзы:

R= (r_k² – r_m²)/((k-m)λ) (5)

Из таблицы выберите три пары колец и вычислите радиус кривизны линзы по формуле (5). Для уменьшения ошибки, вносимой множителем (r_k - r_m), следует выбрать пары колец, наиболее удалённые друг от друга.

7. 
   По трём значениям R вычислите среднее значение радиуса кривизны линзы.
   

8. 
   Замените светофильтр и проведите измерения размеров колец для других длин волн. Вычислите радиус кривизны линзы для каждого значения длин волн.
   

Контрольные вопросы

1. 
   При каких условиях возникает интерференция?
   
2. 
   Каковы условия максимумов и минимумов при интерференции?
   
3. 
   Объясните происхождение колец Ньютона.
   
4. 
   Почему в центре колец в отраженном свете расположено тёмное пятно?
   
5. 
   Чем отличаются картины колец Ньютона в отраженном и проходящем свете?
   
6. 
   Что произойдёт с кольцами, если синий светофильтр заменить красным?
   
7. 
   Что произойдёт с кольцами, если пространство между линзой и пластиной, имеющими показатель преломления n, заполнить жидкостью с показателем преломления n₀?
   
8. 
   Почему ширина колец уменьшается с увеличением порядкового номера кольца?
   

Список литературы

1. 
   Трофимова Т.И. Курс физики. - М.: Высшая школа. 2003, §§ 171, 174.
   
2. 
   Савельев И.В. Курс общей физики. Кн. 4. - М.:Наука,1998, гл.4.
   
3. 
   Ландсберг Г.С. Оптика. □ М.: Наука, 1976. Гл. IV; VI,. 26.
   
4. 
   Сивухин Д.В. Общий курс физики. Т. IV. Оптика. М.: Наука, 1980. Гл. III.
   
5. 
   Дитчберн Р. Физическая оптика. □ М.: Наука, 1965. Гл. V.